有限元理论与Abaqus实现研究：壳的剪切应力分析

==概述==

本系列文章研究成熟的有限元理论基础及在商用有限元软件的实现方式。有限元的理论发展了几十年已经相当成熟，商用有限元软件同样也是采用这些成熟的有限元理论，只是在实际应用过程中，商用CAE软件在传统的理论基础上会做相应的修正以解决工程中遇到的不同问题，且各家软件的修正方法都不一样，每个主流商用软件手册中都会注明各个单元的理论采用了哪种理论公式，但都只是提一下用什么方法修正，很多没有具体的实现公式。商用软件对外就是一个黑盒子，除了开发人员，使用人员只能在黑盒子外猜测内部实现方式。

一方面我们查阅各个主流商用软件的理论手册并通过进行大量的资料查阅猜测内部修正方法，另一方面我们自己编程实现结构有限元求解器，通过自研求解器和商软的结果比较来验证我们的猜测，如同管中窥豹一般来研究的修正方法，从而猜测商用有限元软件的内部计算方法。我们关注CAE中的结构有限元，所以主要选择了商用结构有限元软件中文档相对较完备的Abaqus来研究内部实现方式，同时对某些问题也会涉及其它的Nastran/Ansys等商软。为了理解方便有很多问题在数学上其实并不严谨，同时由于水平有限可能有许多的理论错误，欢迎交流讨论，也期待有更多的合作机会。

iSolver介绍视频：

http://www.jishulink.com/college/video/c12884

==壳的剪切应力 ==

自编有限元应力的校核除了Mises等合力外，也应该校核各个应力分量。材料力学中六个应力分量如下：                  

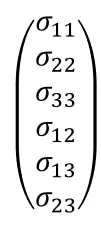
其中Tau11，Tau22，Tau33为正应力，Tau12,13,23为三个剪切应力，对壳来说，Tau33=0，Tau12为面内剪应力，Tau13,23即为本文所说的横向剪切应力。

最近在做iSolver壳的应力分量和Abaqus比对时，发现Abaqus的横向剪切应力和预想的不一致。iSolver按照常用的壳的理论得到的剪切应力是个与厚度无关的常量，但Abaqus的横向剪切应力分量TSHR13，TSHR23，在各个截面方向积分点section point不一样。

花了点时间细致的研究了一下，猜测Abaqus中剪切应力TSHR13、23是真实应力，但有限元理论和iSolver中计算的是板壳近似理论中平均剪切应力。本章将介绍壳单元中实际的和板壳近似理论中的剪切应力，也猜测了Abaqus的内部实现流程，最后通过一个算例来验算Abaqus中的真实的剪切应力，并通过iSolver来计算板壳理论的平均剪切应力。

1.1 壳的真实的剪切应力

剪应力是材料由于抗拒面之间的滑动而产生的沿表面方向的应力。壳的中间层存在剪切应力，这个可以通过下面简单的例子验证。两块板叠加在一起，简支，中点加力，板间假定无摩擦，那么将会得到下面的形状，中间层表面上梁的伸长和下梁的缩短完全由x方向应力决定，此时中间层无抗拒滑动的力，也就不存在剪应力，。

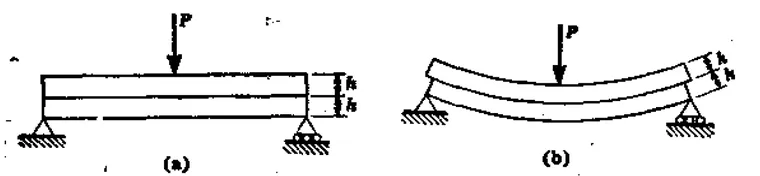
但如果两块板中面部分用胶水粘住，胶水将会阻碍中间层上下两个面的相对滑动，上边面的纤维长度会变少，下边面的纤维长度增加，使得中间层上下两个纤维长度相等，也就在中间层将产生剪应力。

同时，很显然，上图最上层面任意一点没有任何切向的外力，所以不会有阻碍滑动的剪切应力了。而从中间层到最上层，可以猜测剪应力将逐步减小。根据材料力学的理论，实际的截面上的剪应力分布如下：

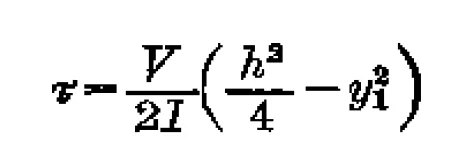
其中V为剪力。

显然与材料点所在截面的y方向坐标y1是二次关系。用图形化表示为下图右侧，随截面厚度方向是抛物线，中面最大，上下表面为0：

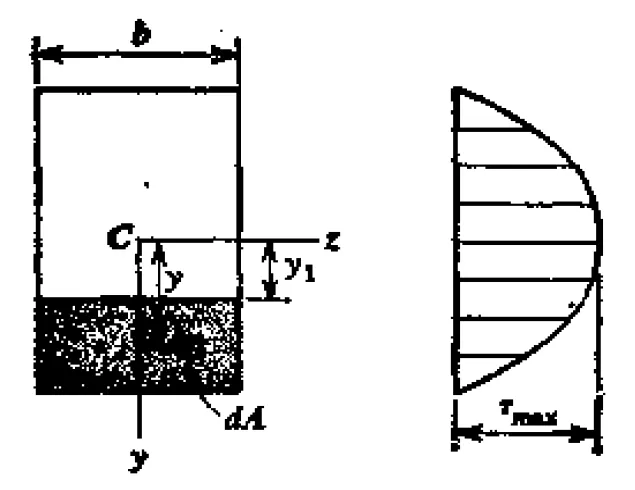
在各向同性材料中，剪切应力和剪切应变也就是剪切角成正比，所以，如果一个橡皮条做成的悬臂梁，那么原来在铅直线上画的直线受力后将会变成如下图所示的m1n1的曲线。

1.2 板壳近似理论的平均剪切应力

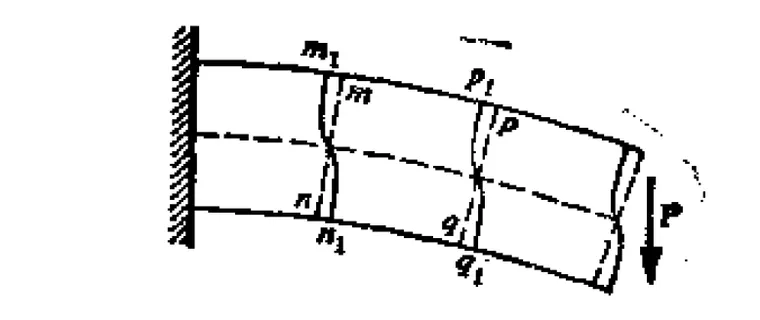
上面的剪切应力表达式中，需要预先知道剪力V，但实际有限元流程中在计算刚度矩阵K时并不知道V，K只由两者决定，一个是应力应变关系，也就是本构关系矩阵C，另一个是应变和位移关系，也就是常说的B矩阵。因此有限元中对壳做了直线法的近似，认为变形前垂直于中面的截面的所有材料点变性后依然位于一个平面内，譬如下图的红色箭头表示原先面上的所有材料点受力后组成新的材料点平面。根据这个假设，那么可以发现所有的剪切角也就是剪切应变是个恒定值，乘以各向同性的剪切模量G，那么得到的剪切应力也是恒定值，相当于一个平均效应的应力，但后面的例子通过iSolver的计算可以看到，这个平均剪切应力并不是简单的是剪力V在截面上的平均。

1.3 Abaqus内部实现流程猜测

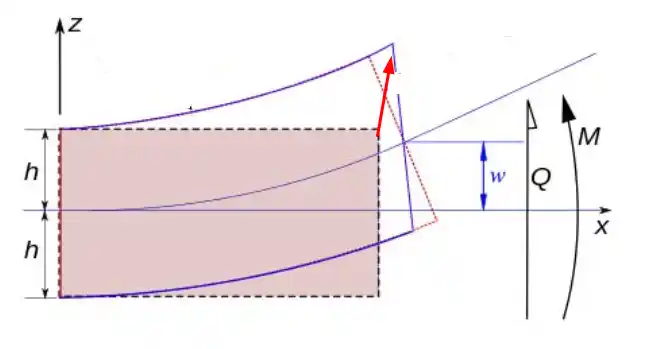
Abaqus程序的内部流程由增量迭代法实现，猜测和普通的有限元理论是一致的，对静力分析步骤如下：

1. 根据本构关系和尺寸得到K。

2. 由外力平衡得到位移d。

3. 由位移d计算内部剪切应力S13、S23，从而得到节点力。

4. 求非平衡力，判断收敛，如果收敛，那么结束。

而S13、S23猜测应该是按板壳近似理论得到的与厚度无关的平均应力，真实的剪切应力并不参与迭代。

在迭代完毕后，如果用户需要输出截面真实的剪切应力，那么根据前面所说的剪力V来计算TSHR13/23。

1.4 算例

我们只能验算Abaqus真实剪切应力TSHR13和23的结果，但没有找到方法来验证用于Abaqus流程的剪切应力是取的平均应力还是真实应力，因为Abaqus的S13，S23没有找到方法输出。但通过自编程序iSolver，我们还是计算了横向平均剪切应力的大小，如果有人也自己编程序，遇到类似问题时可以对比一下结果。

1.4.1 算例说明

只取一个简单的长方形。

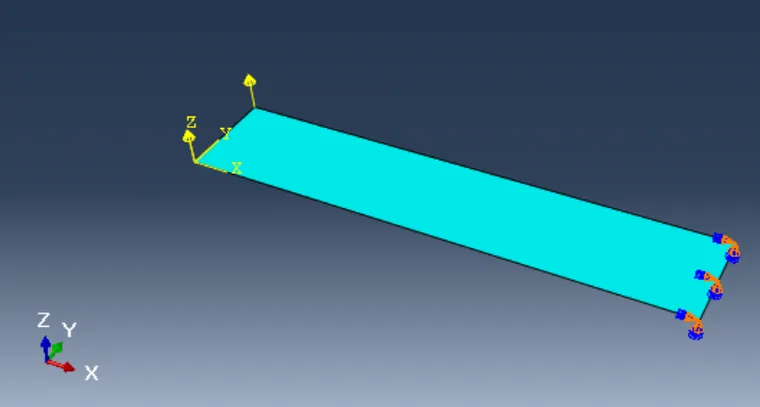
参数如下：

尺寸：5X1，厚度0.1。

材料：Young’s Modulus 1e8， Poisson Ratio 0.3。

右侧两个节点固支。

左侧两个节点每个加集中力1e5，z方向。这样将产生面外弯曲。

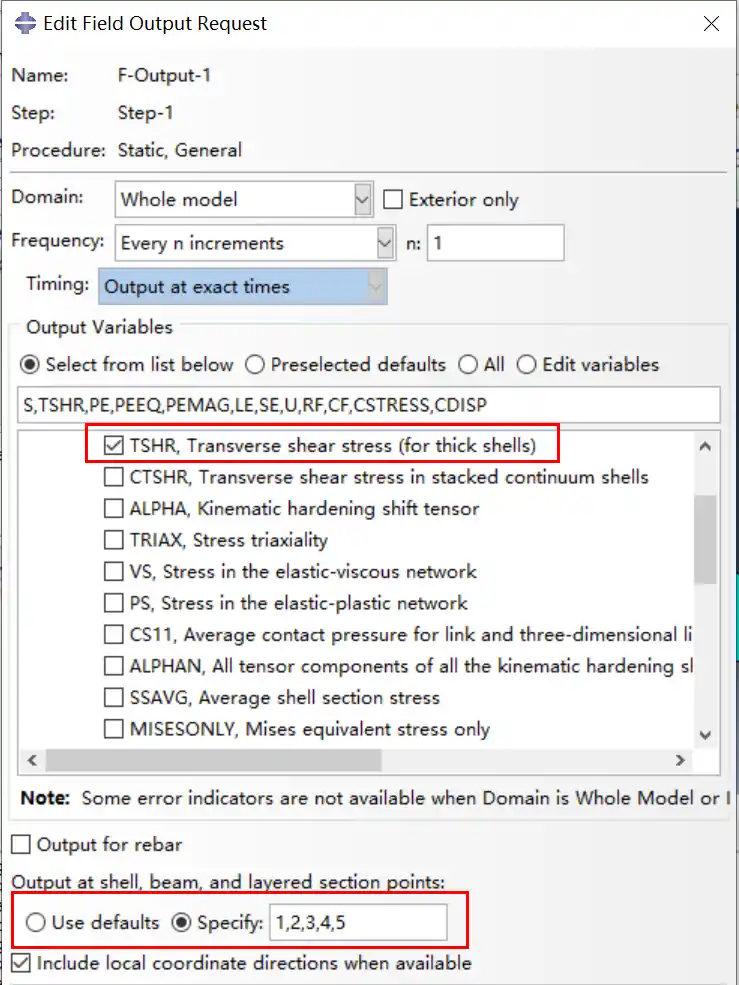
在Step中勾选输出截面应力和输出截面积分点的变量。

1.4.2 中面真实剪切应力理论结果

V=100000*2，b=1，h=0.1

TauMax=3/2*V/(b*h)=3e6

1.4.3 Abaqus真实剪切应力结果

下表面TSHR13=0：

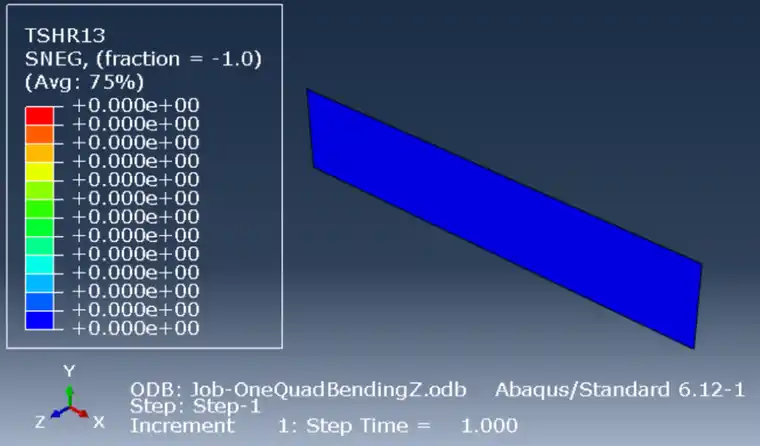
中面为3e6，和理论完全一致。

1.4.4 平均剪切应力结果

Abaqus中无法输出S13和S23，也就是平均剪切应力，为了便于大家理解S13这个值大概是什么量级，我们采用iSolver，在内部计算得到积分点上的剪切应力得到S13=8.1e5，而只有采用平均面积得到的V/(b*h)=2e6的2/5左右，就算加上剪切修正因子5/6也不是简单的按平均面积得到的结果，猜测是因为在这种情况下，壳只在两个节点处加载荷，而不是在一个自由边上均匀加载，而平均面积计算的剪切应力是假定均匀加载得到，所以不一致。当然，有限元中采用这个积分点应力来求节点力，得到的节点力依然和外力是平衡的。

==总结==

本章介绍了壳单元中实际的和板壳近似理论中的剪切应力，也简单猜测了一下Abaqus的内部实现流程，最后通过一个算例来验算Abaqus中的真实的剪切应力。同时还有两个疑问也希望与大家讨论，得到大家的指点。

1）我们暂时没有找到方法来验证用于Abaqus流程的剪切应力是取的平均应力还是真实应力，因为Abaqus的S13，S23没有找到方法输出，不知道谁了解怎么输出壳的这两个应力？

2）按照下面的公式，Mises力应该包括正应力和剪切应力，但查看壳的Mises应力结果可以看出，壳的Mises力没有计入Tau13，Tau23，不知道为什么这样取Mises力？这样用来校核壳的Mises应力达到屈服是否会有问题？

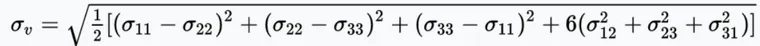
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删