ABAQUS中单元积分点与节点应力转换方法（以CPE4为例）

在ABAQUS中,当需要获取节点上的应力时,可以在后处理中建立路径或者用查询功能等获取.

但是当需要大量的节点上应力数据时,很多人会用Python编程进行大批量的提取应力.但是提取出来的应力为单元积分点上的应力.无法获取节点上的应力.同时在ABAQUS中的子程序中,也是对积分点上的数据进行操作.

本文基于个人兴趣同时想要更加了解有限元背后原理和公式的想法.近日进行了一些初步的探索.希望大家批评指正. 本文基本不涉及原理公式，只在转换积分点和节点的应力时列出公式。尽可能简介易懂。

一: 单元类型及节点数目与位移,应变,应力阶次的关系

本节内容基于有限元教材及一些网上资料.

1)有限元求解的思路是:

一: 建立单元节点力与节点位移关系式.

二: 将弹性体上的外载荷等效移置到节点上.

三: 在节点上建立力的平衡方程,求得节点位移.

四: 通过弹性力学基本方程,可求得单元的应力和应变.

2) 四节点矩形单元

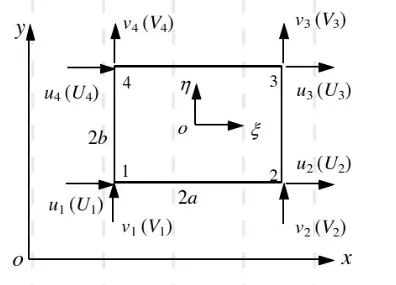
以四节点矩形单元为例，在此只表达有限元教材中的结论，具体公式可参考有限元教材。

3）ABAQUS中的CPE4单元

CPE4:  A 4-node bilinear plane strain quadrilateral.

该单元有四个节点，同时有四个积分点。

对于每个应力分量（注意：在此只看一个应力分量），单元内任一点（x,y）的应力表达式为：

stress=a*x*y+b*x+c*y+d    （1）

该表达式有四个未知量：a,b,c,d。

若知道四个积分点的应力分量。将每个积分点带入上式，则会形成包含四个方程的线性方程组。（注意：变量是a,b,c,d,而不是x,y.所以方程组是线性的）

第一个积分点的应力和坐标：S1，(X1，Y1);

第二个积分点的应力和坐标：S2，(X2，Y2);

第三个积分点的应力和坐标：S3，(X3，Y3);

第四个积分点的应力和坐标：S4，(X4，Y4);

现在的问题是：应力分量S1，S2，S3，S4是已知的，我们需要知道真实的积分点的坐标信息吗？

答案：不需要，只需要知道积分点在整个单元相对位置即可。即等参元中的坐标。（教材中有）

等参元的长和宽都为2.

而有限元中的积分是高斯积分，积分点的位置是固定的。由查表可知：

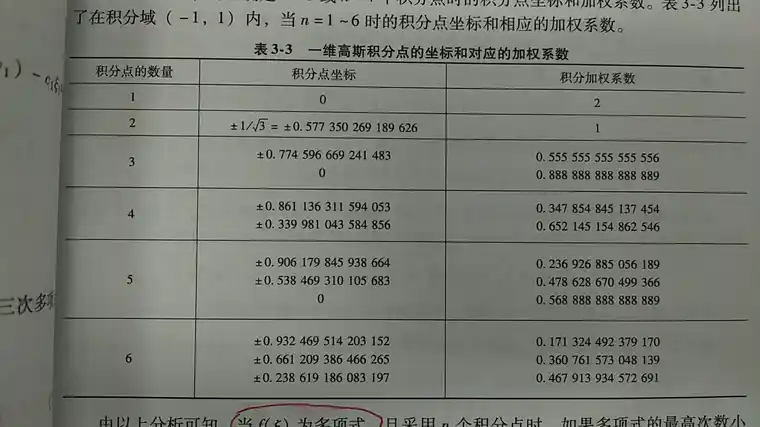
上表是一维的高斯积分点的坐标，后面的加权系数不用管（我们不求积分）。由一维可以猜出二维（两个一维）。二维有4个积分点，所以我们对应一维选第二行的数据。

最终四个积分点在等参元中的坐标如下（顺序目前是乱的，后面需要进一步判断）：

第一个积分点的应力和坐标：S1，(0.577，0.577);

第二个积分点的应力和坐标：S2，(0.577，-0.577);

第三个积分点的应力和坐标：S3，(-0.577，0.577);

第四个积分点的应力和坐标：S4，(-0.577，-0.577);

同时四个节点在等参元中的坐标如下（顺序目前是乱的，后面需要进一步判断）：

第一个节点的应力和坐标：(1，1);

第二个节点的应力和坐标：(1，-1);

第三个节点的应力和坐标：(-1，1);

第四个节点的应力和坐标：(-1，-1);（因为等参元为边长为2的正方形）

4）求节点上的应力

将四个已知的积分点数据代入应力表达式（1）中：

S1=a*0.577*0.577+b*0.577+c*0.577+d

S2=-a*0.577*0.577+b*0.577-c*0.577+d

S3=-a*0.577*0.577-b*0.577+c*0.577+d

S4=a*0.577*0.577-b*0.577-c*0.577+d

换成矩阵形式：

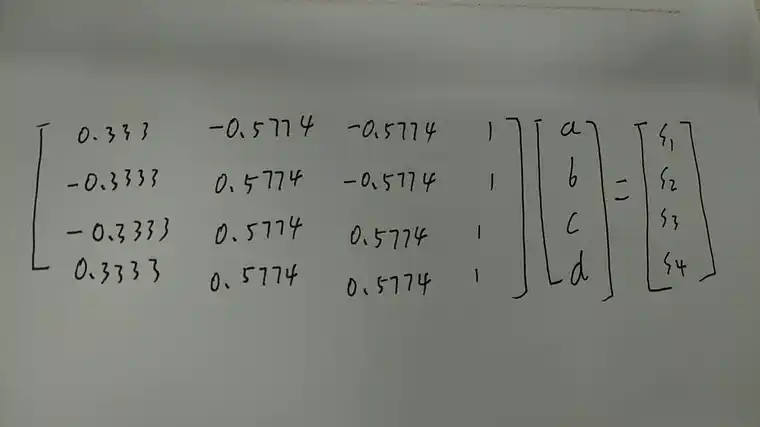
求该线性方程组即可得出系数：a,b,c,d和应力的表达式。

然后将节点坐标代入表达式即可求出相应节点的应力。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删