==概述==
在CAE领域,从学校、实验室的自研算法到实现真正的商业化软件是一条无比漫长的道路。我们不研究有限元的新方法、新理论,只是研究商用有限元软件的实现方式。有限元的理论发展了几十年已经相当成熟,商用有限元软件同样也是采用这些成熟的有限元理论,只是在实际应用过程中,商用软件在这些传统的理论基础上会做相应的修正以解决工程中遇到的不同问题,且各家软件的修正方法都不一样,每个主流商用软件手册中都会注明各个单元的理论采用了哪种理论公式,但都只是提一下用什么方法修正,很多没有具体的实现公式。
商用软件对外就是一个黑盒子,除了开发人员,使用人员只能在黑盒子外猜测内部实现方式,一方面我们查阅Abaqus软件手册得到修正方法的说明,另一方面我们自己编程实现简单的结构有限元求解器,通过自研求解器和Abaqus的结果比较结合理论手册如同管中窥豹一般来研究Abaqus的修正方法,从而猜测商用有限元软件的内部计算方法。为了理解方便有很多问题在数学上其实并不严谨,同时由于水平有限也可能有许多的理论错误,欢迎交流讨论。
商用有限元软件的健壮性体现在对各种特殊情况,求解过程和解的正确性依然能得到保证,而这些特殊情况在自编程序中如果没有考虑到,那么结果就可能相差极大。其中剪切自锁和沙漏现象是最常见的会影响正确性的两个特殊情况。这两者具有相似性,所以我们在本文中一起研究Abaqus中线性壳单元S4针对这两种情况下的内部实现方式。剪切自锁和沙漏现象影响的是刚度矩阵和应力,我们研究方式是在自编程序iSolver中根据成熟的消除剪切自锁和沙漏控制的理论实现刚度矩阵的修正,通过比较同一模型的Abaqus的刚度矩阵结果,结合帮助文档猜测Abaqus软件单元消除剪切自锁和控制沙漏的内部实现方法。
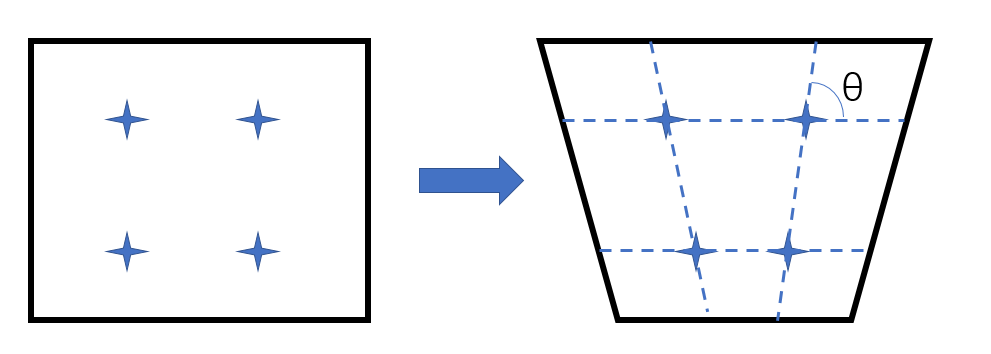
图1:剪切自锁
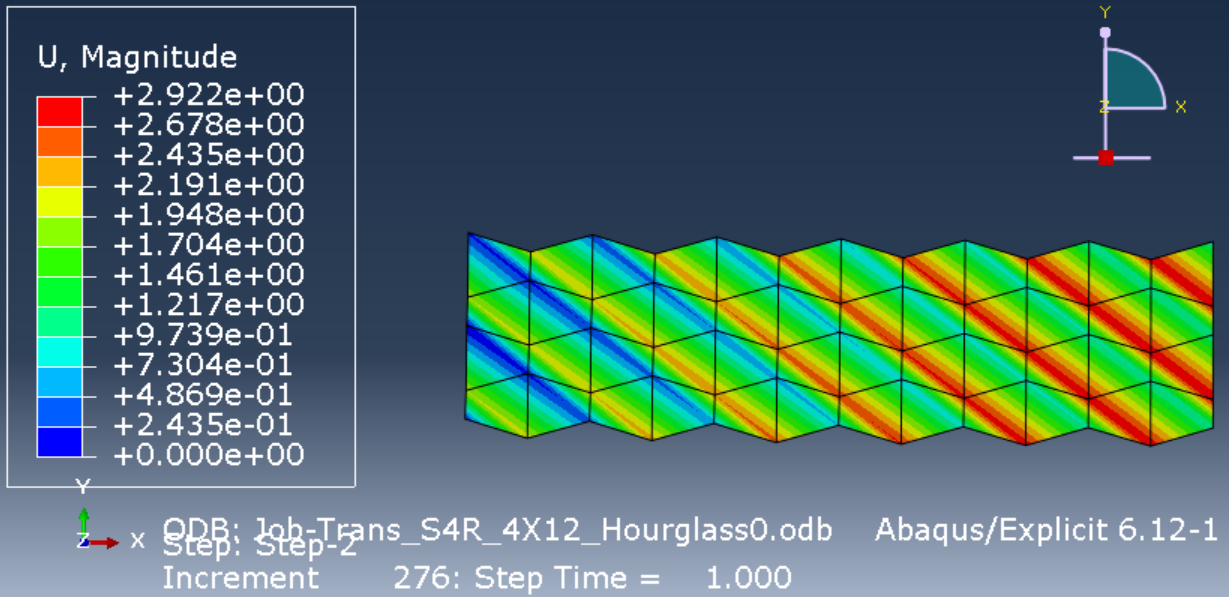
图2:沙漏
完全积分单元才有剪切自锁,虽然Abaqus的S4单元是完全积分,但内部已经做了修正完全消除了剪切自锁,所以不需要用户做任何设置。
减缩积分单元才有沙漏现象,Abaqus的S4R默认增加一个人工的沙漏刚度来控制沙漏现象,如果发现结果还是不理想,那么需要采用其它建模方法才能控制沙漏了。
Abaqus针对剪切自锁和沙漏控制做的修正如下:
| 单元类型 | 元素 | 修正情况 | |
| 剪切自锁 | S4 | 薄膜刚度 | 假设应变方法修正 |
| 面外弯曲刚度 | 无 | ||
| 面外横向剪切刚度 | 假设应变方法修正 | ||
| S4R | 所有项 | 无 | |
| 沙漏控制 | S4 | 薄膜刚度 | 无 |
| 面外弯曲刚度 | 无 | ||
| 面外横向剪切刚度 | 沙漏控制,和Belytchko公式不一致,暂时没研究 | ||
| S4R | 薄膜刚度 | 和Belytchko公式一致,因子取0.005G | |
| 面外弯曲刚度 | 和Belytchko公式一致,因子取0.00375G*4 | ||
| 面外横向剪切刚度 | 沙漏控制,和Belytchko公式不一致,暂时没研究 |
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删