本系列文章研究成熟的有限元理论基础及在商用有限元软件的实现方式,通过
1) 基础理论
2) 商软操作
3) 自编程序
三者结合的方式将复杂繁琐的结构有限元理论通过简单直观的方式展现出来,同时深层次的学习有限元理论和商业软件的内部实现原理。
有限元的理论发展了几十年已经相当成熟,商用有限元软件同样也是采用这些成熟的有限元理论,只是在实际应用过程中,商用CAE软件在传统的理论基础上会做相应的修正以解决工程中遇到的不同问题,且各家软件的修正方法都不一样,每个主流商用软件手册中都会注明各个单元的理论采用了哪种理论公式,但都只是提一下用什么方法修正,很多没有具体的实现公式。商用软件对外就是一个黑盒子,除了开发人员,使用人员只能在黑盒子外猜测内部实现方式。


一方面我们查阅各个主流商用软件的理论手册并通过进行大量的资料查阅猜测内部修正方法,另一方面我们自己编程实现结构有限元求解器,通过自研求解器和商软的结果比较来验证我们的猜测,如同管中窥豹一般来研究的修正方法,从而猜测商用有限元软件的内部计算方法。我们关注CAE中的结构有限元,所以主要选择了商用结构有限元软件中文档相对较完备的Abaqus来研究内部实现方式,同时对某些问题也会涉及其它的Nastran/Ansys等商软。为了理解方便有很多问题在数学上其实并不严谨,同时由于水平有限可能有许多的理论错误,欢迎交流讨论,也期待有更多的合作机会。

从NASA在1964年推出Nastran算起,结构CAE软件已经发展了将近60年,虽然在60年内商用结构软件层出不穷,但最流行的通用结构CAE软件现在依然只有Nastran、Ansys和Abaqus三款软件,iSolver以前的结果精度完全对标Abaqus,线性和材料非线性与Abaqus计算结果对比精度已经没有误差,但在推广过程中,发现在线性问题上,客户只相信Nastran的结果,因为很多工程的校核规范和经验方法都以Nastran的结果为基准,如果换成其它软件,那么那些经验系数和校核公式都可能会修改,而这些修改还需要做大量的工程验证,这是客户承受不了的代价。客户改不了的习惯只能是自主软件改,我们的自主软件只是一个后来者,想要推广只能按客户要求修改精度,因此,iSolver开始兼容Abaqus和Nastran的精度,计算出的结果既可以对标Abaqus,修改设置后又可以对标Nastran,因此需要对Abaqus和Nastran的各方面的算法差异进行深入研究。如果是线性问题,那么Nastran和Abaqus的精度误差主要体现在单元算法、边界处理、MPC约束关系等,在2017年第二篇:S4壳单元质量矩阵研究文章中我们就曾经分析过Abaqus的S4壳单元和Nastran的Quad4壳单元质量矩阵的内部实现方式和差异,在这里主要研究Abaqus、iSolver与Nastran梁单元差异,由于这三款软件的梁单元的差异较多,我们分几篇文章来说明,本篇是Abaqus、iSolver和Nastran梁差异(4)-形心、剪心和偏置。


一根梁虽然在有限元内部计算时采用线单元表示,但实际上只是把梁的三维形状简化到了参数中,如果显示一个梁的具体形状,譬如典型的T型梁:
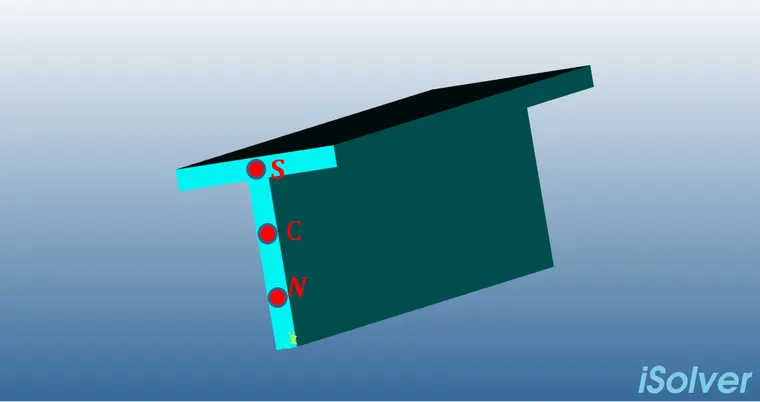

将会有下面三个特殊点:
1)形心C
就是的二维截面几何图形的重心。
2)剪心S
剪心为两个截面方向的集中力都不会导致扭转的交点。譬如槽钢的剪心S大体如下,显然和形心C不是同一点:

如果在y方向加集中力,可发现只有通过剪心才能不发生扭转,即下方的第二图:



3)节点位置N
节点位置就是建模时输入的位置,譬如下面的三个节点就是0,0,0、100,0,0,和200,0,0
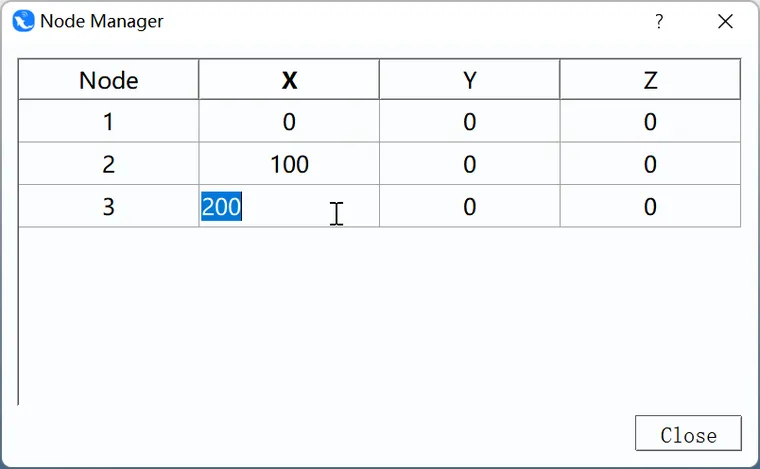

那么在CAE软件中就是线显示的位置:
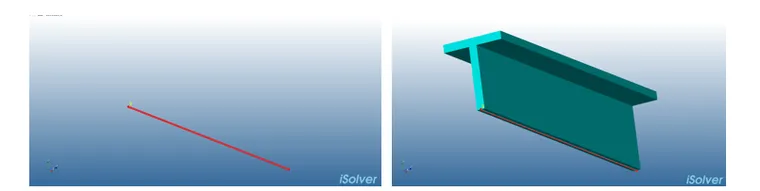


既然梁简化为线单元的过程中有三个特殊点:形心C、剪心S和节点N,那么问题来了:
1) 输入的力加载在什么位置?
2) 计算采用的运动的相对位置是什么?
梁单元截面上的加载就是集中力、yz方向的弯矩,x轴的扭矩,我们分开讨论:
对于集中力,实际生活告诉我们一根手指去压迫梁截面,那么手指和截面接触的位置显然就是加载点。
实际力和力矩可以加载到任意点上,只要和实际的力和位移关系一致就行,但有限元让用户输入集中力和力矩时没有输入截面坐标,只可能默认是上面三个特殊点之一。
具体加载到什么位置可以做个简单的实验证明:
Example1:Ex1-LoadPosition\
譬如上面的T型材,如果将节点位置N改到剪心S上方(实际不是改节点位置,而是改偏置)
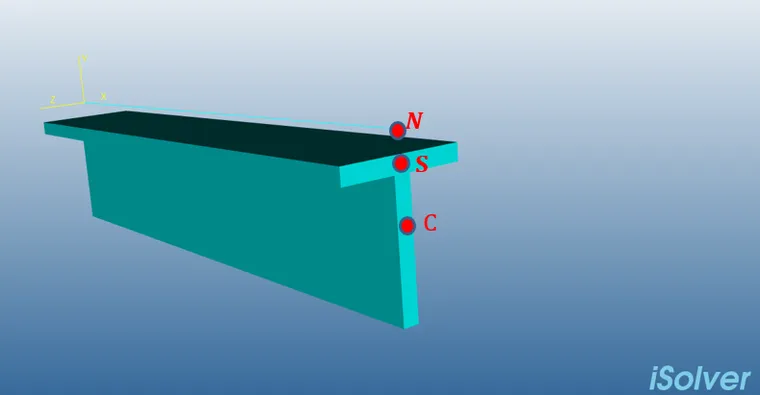

将左端固定,右端在z方向加集中力载荷。


那么,可能如下:
1) 如加载到形心C,右侧节点2绕x轴逆时针旋转,得到扭转角度UR1<0
2) 如加载到节点位置N,右侧节点2绕x轴顺时针旋转,得到扭转角度UR1>0
3) 如加载到剪心位置N,不旋转,得到扭转角度UR1=0
在iSolver中计算如下:

可发现UR1>0,说明是加载到节点上的。
力矩在有限元中和力一样都是加载到过节点N的转动轴上,注意力矩是输入,与梁实际的转动轴无关。譬如下图节点如果在底部,那么力矩M通过力F*到节点的距离应该表示为下图所示:
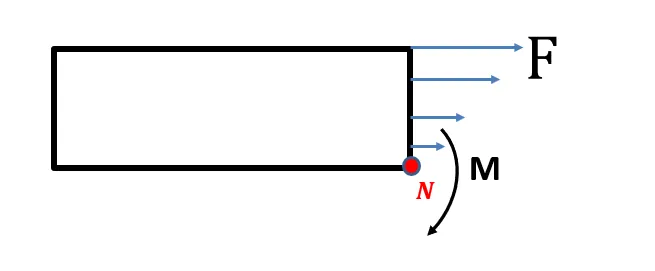

我们查看Nastran的帮助手册,也可发现Nastran的集中力也是加载在节点Grid上。


所以,集中力和力矩就是加载在节点Node所对应的N(x、y、z)上,只不过N(x、y、z)可能恰好是剪心,也可以是形心,当然,也可能是不在这两个点上的任意值。
力的加载位置和梁的真正后台计算的相对位置不同,梁的运动分为平动、绕x轴的扭转、绕y/z轴的弯曲转动,平动显然是节点本身的运行,不做讨论,但转动是绕转动轴运动的,这个转动轴和输入的力矩认为转动轴不是一回事,由上面讨论输入的力矩认为转动轴总是过节点N的,但这边运动的转动轴是软件内部计算采用的转动轴,每个软件还是不同的。
有限元中,如果受到剪心位置的扭矩,那么扭转角沿过剪心的x方向轴计算。


即J中的距离是相对剪切中心来计算。
当剪心不在节点上时,无论材料力学理论还是Abaqus/iSolver/Nastran软件会认为扭转轴还是绕过剪心的轴线,而不是过节点的:
此时,显然J不变,但需要把节点的扭矩和扭转角变换到剪心。
当一个集中力矩移动到另一点时,力矩和扭转角度都不会变,但绕剪心的旋转对节点导致截面两个方向的位移v、w的变换,且显然与剪心和节点的距离NS有关,具体这个v、w的变换如何影响刚度也可看我们以前梁单元刚度阵的文章。
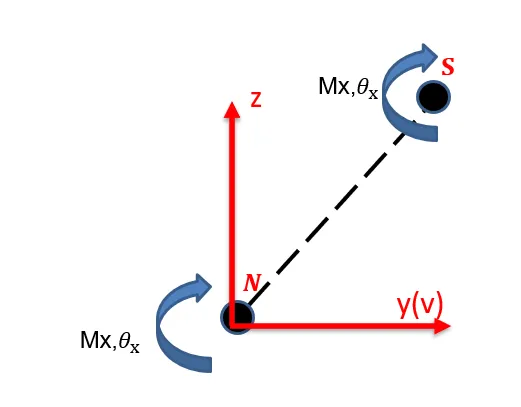
弯矩是绕某个轴的旋转,我们来分析究竟绕过节点还是形心旋转?
我们先从一般的弯矩公式的最原始的推导说起,在受弯矩作用下,梁做纯弯曲变形,整个梁的每条平行与轴线方向的纤维都弯曲为圆形。
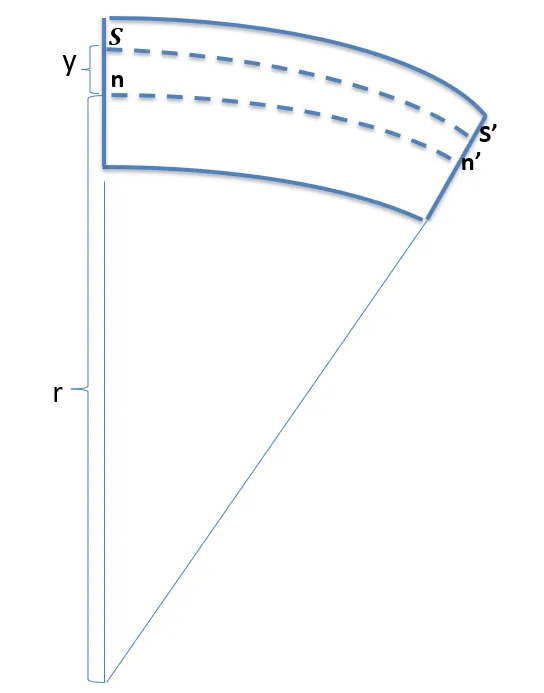

那么纤维SS’的相对nn’的升长量是
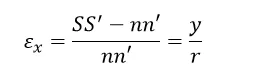

如果nn’是中性轴,也就是nn’的长度就是纤维SS’原来的长度,那么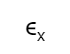
 就是SS’的应变。由应力应变关系:
就是SS’的应变。由应力应变关系:
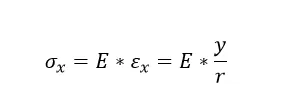

内外力矩平衡:
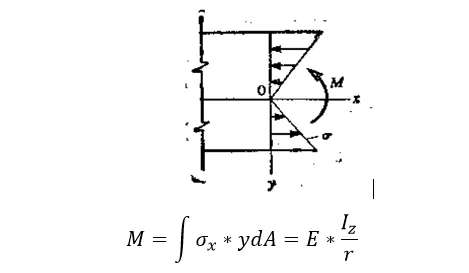


其中:Iz为
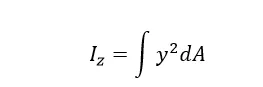

得到应力:
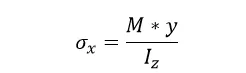

材料力学书中一般认为y表示所在截面点到中性轴的y位置,也就是说弯曲是绕中性轴的运动。
但从上面的推导可以看出,要上面的公式成立:需满足:
1.纯弯曲情况。
2.满足中性轴nn’是纤维SS’的没有载荷时的原始长度。
3.弯曲后截面依然垂直中性面,否则下面等式不成立,也就是说只适合Euler梁。
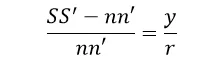

实际的情况很多时候都不是纯弯曲,同时中性轴也会拉伸,所以到底绕哪个轴弯曲每个软件也不同,Abaqus中取的是过节点的弯曲轴,取过节点的好处是由于上面说到的集中力和位移等都是节点的物理量,这样所有的物理量都是节点上的,不用变换。相当于截面上力的内矩采用下图表示:
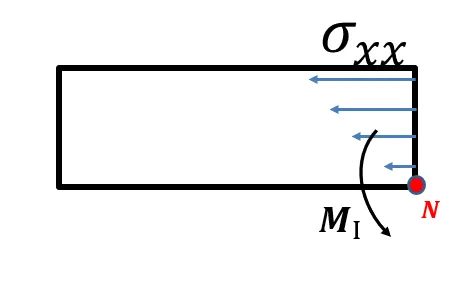

而Nastran中弯曲轴就不同了,取的是形心的弯曲轴。类似于软件内部要做两步操作:
(1) 先将计算转动轴放到中性面:

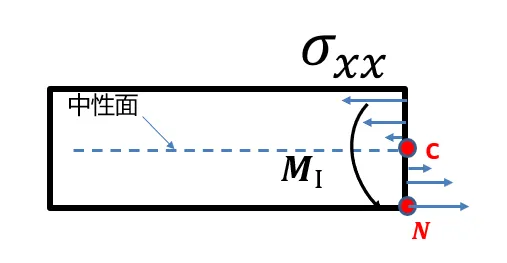
(2)和上面的扭转一样,Nastran的梁单元在后台需要将形心的位移转换到节点上,譬如下方在形心处的弯曲角度θ会导致x方向的位移:
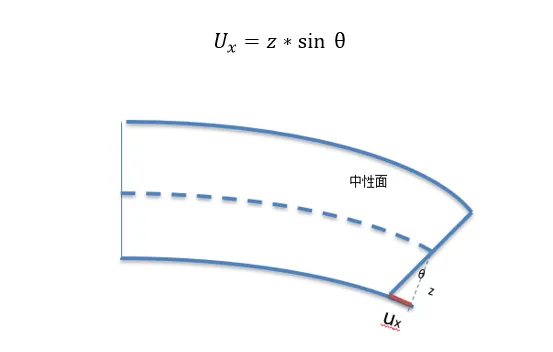


实际的弯矩外力是加在过节点Node还是形心的轴向的呢?也就是说梁的截面是沿哪个轴弯曲的呢?个人没做过实际的物理试验,只是查了一下力矩的加载方法,一种加载方式是在梁的两个边缘加力,然后用力乘以离弯曲轴的距离当做力矩。但试验室截面到底是观测到过节点还是过形心个人理解很难说的清楚,如果问一个小朋友,看上面的弯曲图,转动角度θ是绕哪个轴旋转,也许很多人就会说是底部,而不是中性轴,也就是说从外形上很难确定哪个轴旋转,或者你可以认为是绕任意一个轴旋转。
那么有限元中这两种方式模拟结果是不是一致呢? 我们只以一个简单的例子来说明一下。
Example2:Ex2-TBeamNodeInShearCenter\
我们还是以T型材的一个梁单元为例。
先在iSolver中建模,为减少横向剪切刚度的影响,我们梁长度L取为240,仅取一个单元。
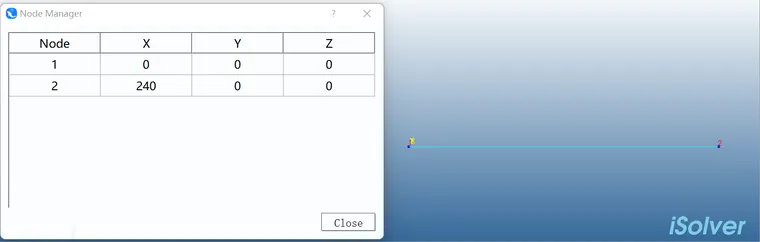

材料杨氏模量=1.5e6,泊松比=0.3。


节点在剪心处,此时T型材的截面尺寸和偏置如下:
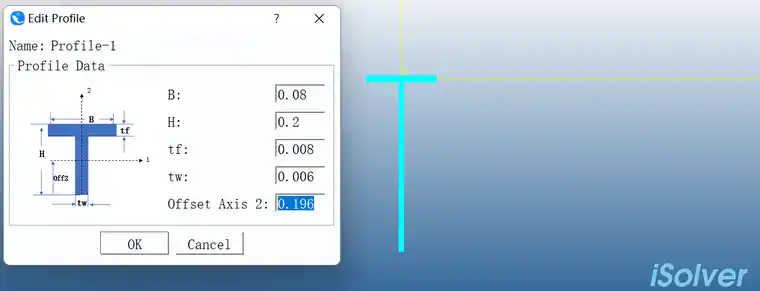

右端全约束,取三种工况:
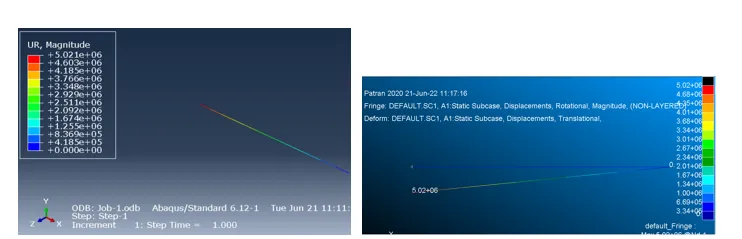
工况(1):左端自由加力,加y-方向集中力F=1:


iSolver导出到Abaqus B31单元和Nastran的CBEAM单元绕z轴转动角度UR3结果都是5.02e6,如下:


工况(2):左端自由加力矩,加z+方向力矩M=1:


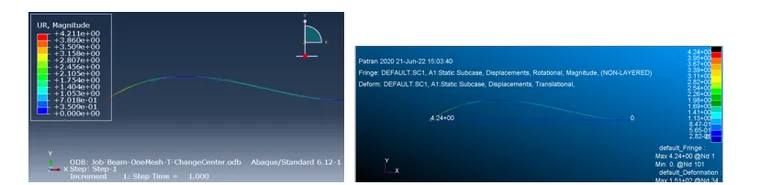
iSolver导出到Abaqus B31单元和Nastran的CBEAM单元UR3结果都是2.09,如下:



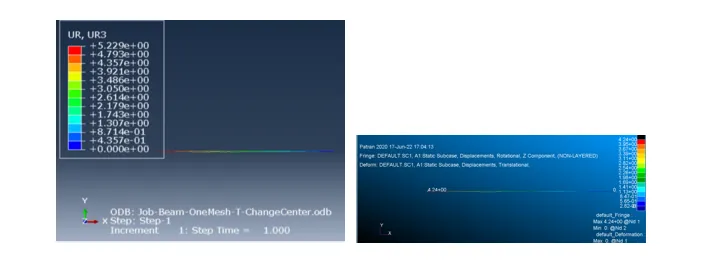
工况(3):在工况(2)的基础上左端简支


Abaqus B31单元和Nastran的CBEAM单元UR3结果分别是5.229和4.24,如下:

明显工况(1)和(2)采用经过节点的弯曲轴的Abaqus和采用经过形心的弯曲轴的Nastran结果基本一致,但工况(3)明显差异较大。我们没有严格的证明,我们猜测无论采用哪个弯曲轴都是正确的,只是多一个平动位移的变换,都是严格满足梁的外力矩=内力矩,外力=内力的关系的。所以(1)和(2)的结果一致,但如果像工况(3)把平动位移约束,弯曲轴的不同导致的差异可能就非常大了。
进一步,对于工况(3),Abaqus和Nastran那么哪个更正确呢?或者谁更可信呢?当我们划分为100个梁单元时,发现Abaqus和Nastran的UR3结果均是4.2左右,我见过这个问题的理论值都是建立在节点在形心位置的,至于现在节点不在形心的情况,没找到对应理论值,只能猜测4.2就是比较精确的实际工程值,那么回头看如果仅仅是一个单元,那么Nastran更精确,当单元足够多时,Nastran和Abaqus结果都一致。


最后我们聊一下形心和剪心位置相关的偏置。
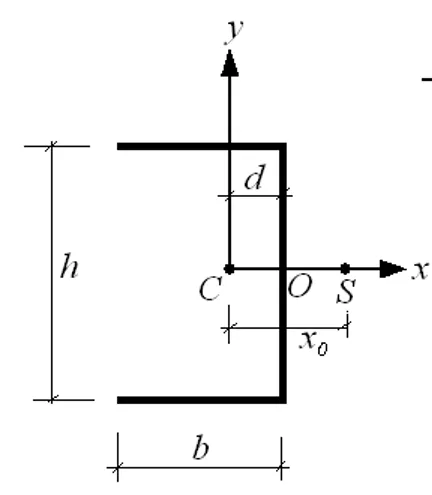
形心和剪心具体是在截面几何图像上哪个点完全由几何形状决定,但形心点和剪心点在三维空间的坐标与这个梁的空间摆放位置有关,在有限元中,这个空间摆放位置由两个参数决定:
1) 节点N的位置决定整体几何截面的2D面。
2) 偏置Offset决定形心/剪心相对节点N的位置。
节点N相对简单,用户设置多少就是多少,但偏置Offset每个软件中的设置不同。
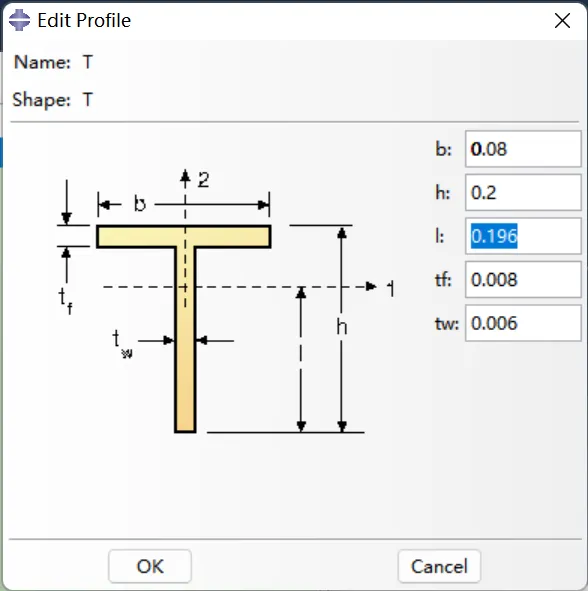
Abaqus的偏置只有一处地方,就是在设置型材的时候设置Offset的参数,譬如T型梁中设置I:

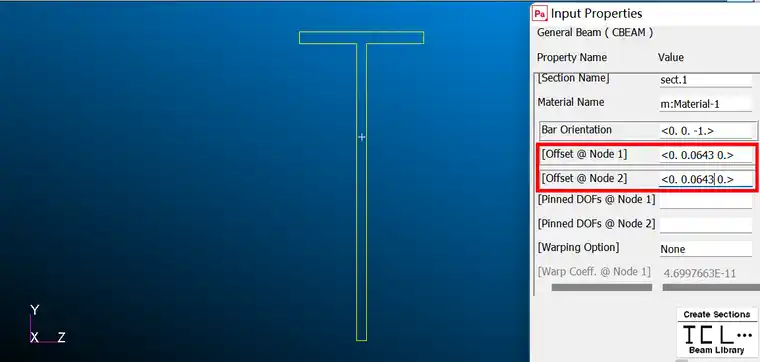
Nastran的Offset有两处:
1) 在单元Property时设置Offset,它默认是全局坐标系的,后台是对CBEAM和CBAR关键词修改,表示单元的偏移。

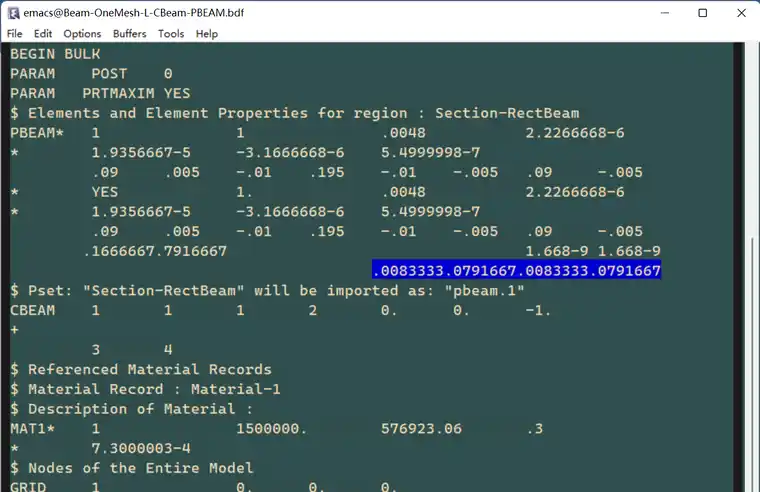
2)单独在PBEAM中设置Offset,此时Offset是相对型材截面局部坐标系的,表示形心的移动,在BDF中PBEAM关键词中可以修改,没找到界面的修改地方,个人基本不用,不是很懂。

Nastran相比Abaqus的优势:
1)Nastran所有的型材都可以设置偏置,而Abaqus很多型材如果要偏置就非常麻烦,譬如Rectangle没有偏置,只能采用Trapzoid中设置上下底相等或者采用Arbitrary梁。
2)看上面解释可对形心和节点分别设置偏置,个人想不出应用场景,总觉得型材安装位置应该只能整体移动,而不是节点和形心可以分别移动。
Nastran相比Abaqus的劣势:
很多实际情况是型材和下面的安装的蒙皮的相对位置是定的,但在三维空间的位移是变化的,所以个人觉得Abaqus的相对坐标系的偏置更实用一点。
也正是基于Abaqus和Nastran的优缺点考虑,iSolver采用了Abaqus的局部坐标系的偏置,同时和Nastran一样可以对矩形或者L型等设置双向偏置。当然,更好的设置偏置的方式是自动偏置,这是Nastran和Abaqus均没有的功能。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删