本系列文章研究成熟的有限元理论基础及在商用有限元软件的实现方式,通过
1) 基础理论
2) 商软操作
3) 自编程序
三者结合的方式将复杂繁琐的结构有限元理论通过简单直观的方式展现出来,同时深层次的学习有限元理论和商业软件的内部实现原理。
有限元的理论发展了几十年已经相当成熟,商用有限元软件同样也是采用这些成熟的有限元理论,只是在实际应用过程中,商用CAE软件在传统的理论基础上会做相应的修正以解决工程中遇到的不同问题,且各家软件的修正方法都不一样,每个主流商用软件手册中都会注明各个单元的理论采用了哪种理论公式,但都只是提一下用什么方法修正,很多没有具体的实现公式。商用软件对外就是一个黑盒子,除了开发人员,使用人员只能在黑盒子外猜测内部实现方式。

一方面我们查阅各个主流商用软件的理论手册并通过进行大量的资料查阅猜测内部修正方法,另一方面我们自己编程实现结构有限元求解器,通过自研求解器和商软的结果比较来验证我们的猜测,如同管中窥豹一般来研究的修正方法,从而猜测商用有限元软件的内部计算方法。我们关注CAE中的结构有限元,所以主要选择了商用结构有限元软件中文档相对较完备的Abaqus来研究内部实现方式,同时对某些问题也会涉及其它的Nastran/Ansys等商软。为了理解方便有很多问题在数学上其实并不严谨,同时由于水平有限可能有许多的理论错误,欢迎交流讨论,也期待有更多的合作机会。
==线性瞬态动力学==
稳态和瞬态都是在随时间变化的激励作用下产生的运动形式,其中,稳态是时间足够长后,系统慢慢趋于稳定后的运动,譬如当不考虑阻尼时弹簧受瞬间载荷力作用时间足够长后最后会做简谐振动,由于简谐振动的理论公式比较简单,一个简谐振动在时间域上虽然很长,但只要有频率和振幅参数就能完全表示,所以可以跳过前面的不稳定的过程而直接求解最终的稳态形式。但达到稳态前的瞬态过程中间每个时刻点的运动状态是不一样的,无法简单的用几个参数表示,当前时刻的运动状态需要前面运动状态往前推进得到,此时只能用瞬态分析。

瞬态分析有线性和非线性之分,从线性瞬态动力学出发其实更容易理解瞬态动力学的求解方式。本章我们将简单介绍一下瞬态动力学的求解公式,并以一个单摆例子来说明线性瞬态动力学在有限元软件中的内部实现原理。非线性瞬态动力学的原理将在后面章节介绍。
线性瞬态动力学的运动方程和线性静力平衡方程很类似,对于线性静力问题载荷F和位移u是直线关系,可以非常简单的由一个状态类乘以一个系数推到另一个状态。因为静力学可以简单的表示为下方的线性表达形式:
Ku=R

譬如下面的悬臂梁问题,载荷1N的时候计算得到最大位移时1.177mm。
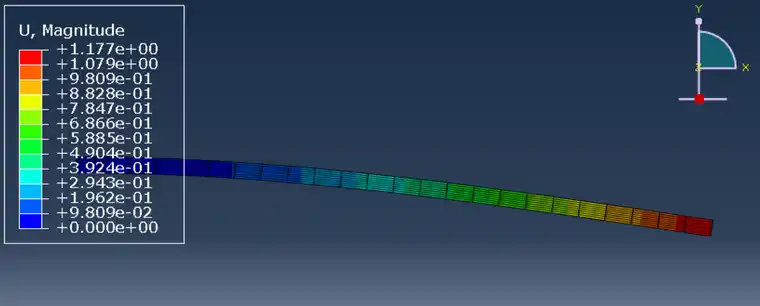

如果载荷是1000N时,不用计算也知道就是最大位移会变为1000倍=1177mm。
但在线性动力学问题中分析复杂一点就是,如果力扩大了1000倍,显然最终的位移不是简单的乘上1000,瞬态动力学和上式原理上很类似,只不过包括了质量阵M相关的惯性力项和阻尼阵C相关的阻尼力项,如下:
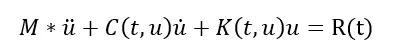

一般质量矩阵与时间和位移无关,而K和C如果和位移和时间无关,那么就是线性瞬态问题。为简单起见,我们不考虑阻尼项。得到如下表达式:
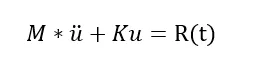

位移和加速度与t相关,上述方程就有两个未知数位移和加速度,只有一个方程是无法求出的,所以还有一个加速度和位移的约束关系,实际中必然是加速度先和速度相关,速度再和位移相关。
在理论上当前时刻的加速度就应该只和当前时刻的位移相关了,但在计算机的数值求解时,无法求出无限个连续时刻的结果,所以只能把整个时间人为的分成多个时间段,方程变为如下:
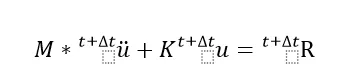

此时,加速度就必须要通过起码两个时刻的速度或者位移才能计算出来的,可以有不同的取法,取前时刻还是后时刻的位移来决定加速度就有隐式和显式之分(具体可看系列文章13:显式和隐式的区别),任何一种分析理论上都可以得到正确解,只不过显式不用求刚度,隐式需要求解刚度阵,而通过刚度的解释可以更容易理解Abaqus内部的实现原理,在本章中,我们选用隐式瞬态分析。
在隐式方法中,将时间离散,加速度表示为位移的表达式后,得到下方的公式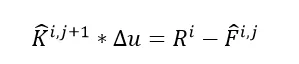

其中K和F在静力学的增量迭代法中表示切线刚度阵和内力,只不过这边需要加上M项:
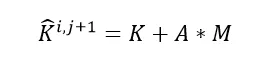
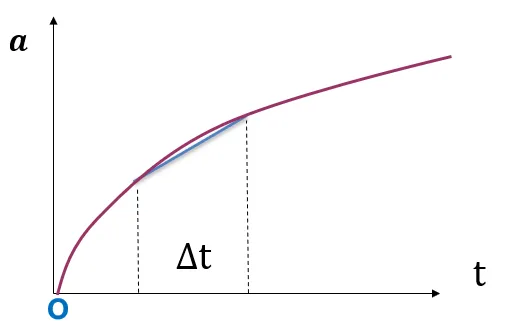
其中A是只与时间增量步相关的量,对不同的隐式算法A的值不同,譬如对最简单的Newmark方法中的梯形隐式算法,加速度在增量步内线性变化,下方红线是在输入的载荷转换为加速度的值,但计算中没法处理连续的曲线,所以Abaqus或者iSolver等有限元程序实际上只会认为增量步 内加速度时线性变化的:
内加速度时线性变化的:

此时得到的修正刚度为:

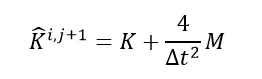
显然当时间增量步固定时,此时的K也是个定值。而F与上一时刻的包括惯性力在内的内力,与位移、速度、加速度相关,可以表示为:
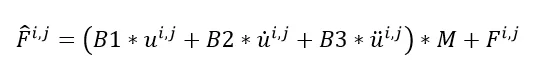

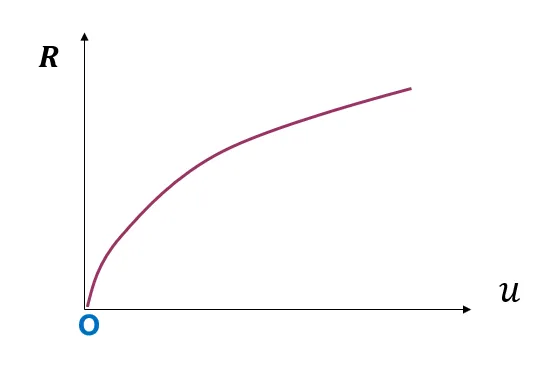
其中B是只与时间增量步相关的量。虽然固定步长K是常量,但右端量还包括了上一个时刻位移、速度等变量,R和u依然为非线性曲线,如下:

由上面的表达式,K和F只与增量步I,j相关,但实际上只要一次迭代左右就能相等平衡了,这个原理就和线性弹性力学的内力F=KU,到时右端在第一个迭代完成后就和外力R一样了,具体可看下面的课程推导:
也就是说线性瞬态动力学方程与迭代步j无关,无须迭代,方程可以简单的写成:
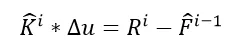

而且只要迭代一次,而且内力项在第一次是位移为0,那么右端F就可以简单的写成下方表达式:
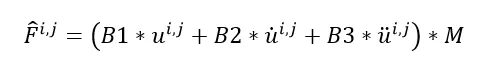

下面我们将以一个简单的单摆模型例子来说明上述线性瞬态动力学的解法。
实际的单摆如下图,线长L,无质量,末端绑定一个质量块m,如果没有空气阻力,在重力加速度g作用下往复运动。我们取初始时刻绳索在水平位置。假定绳索足够硬,在小球作用下变形非常小。显然,这个问题是一个大位移大转动小应变的几何非线性问题(具体可看我们的系列文章18:几何非线性的应变),这个小球位置随时间变化的运动过程就是非线性的瞬态过程。
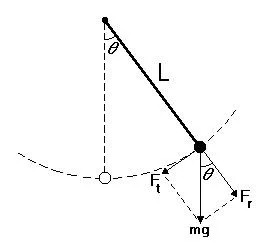

Abaqus中没有绳索单元,我们用Truss杆单元模拟


参数如下:
>尺寸:L=300,Truss截面积1。
>材料:Young’s Modulus 1e10, Poisson Ratio 0。
>边界:左侧节点固支。
>载荷:右侧节点加集中Mass=10,加速度取980,-Y方向。
>网格:划分为一个Truss单元。
>分析步:时间长度取单摆从水平开始回到水平位置一个周期的时间。单摆运动如果摆动幅度很小时,周期可由下式得到,与材料和小球质量无关,这其实也是在地球上的所有钟摆只需通过设置绳长就能精确计时的原理。
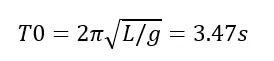

在我们这个例子中,由于是从水平位置开始摆动,所以周期略大于此值,查文献可知周期T=4.12s,增量步固定为0.1。
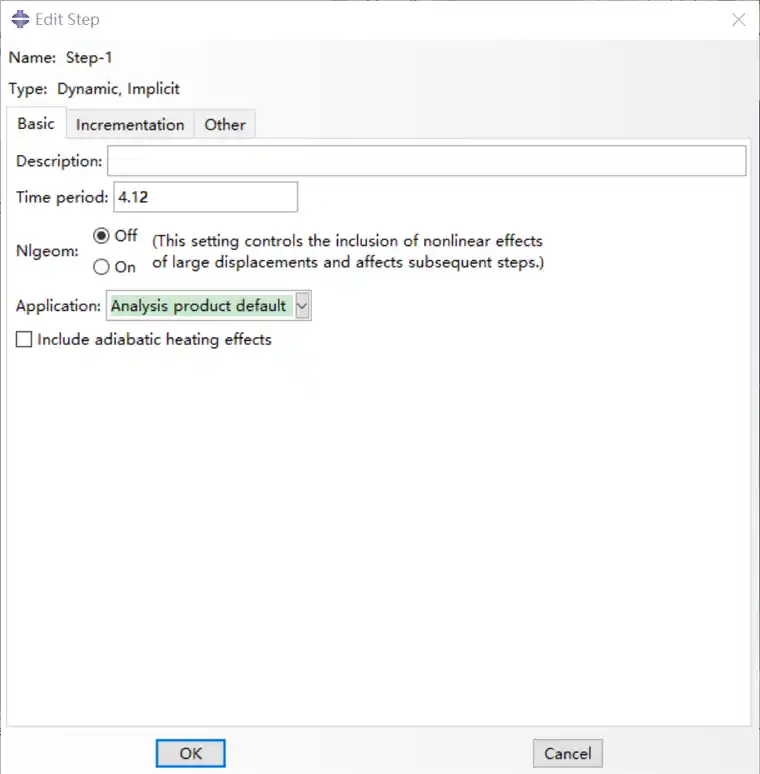

我们研究线性情况下是什么变化过程。在Abaqus中NLGeom=Off,取线性分析。
分析后得到U1、U2在某两个特定时刻结果如下:
0.1s时刻:


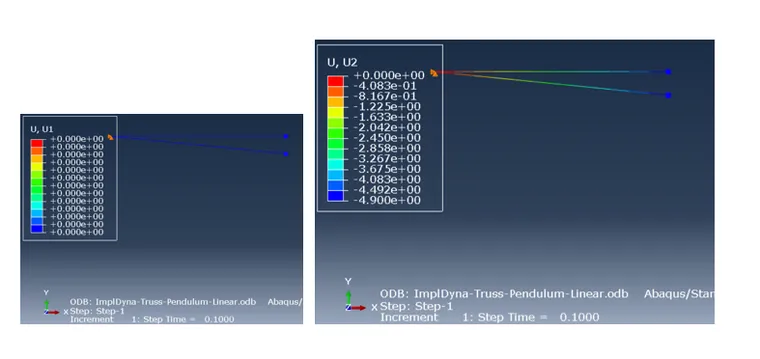
1s时刻:



由上图可知U1永远都是0,而U2会随着时间不断的增加,也就是说不会产生实际的单摆运动。
对一个truss单元来说,它的每个节点都是三个平动自由度,那么两节点truss的K就是一个6X6的矩阵,同时由于左端固支,所以,只剩右端的三个自由度相关的刚度阵,同时,因为我们几何非线性没开启,那么刚度都是初始时刻水平位置的值,此时只有K11有值,质量单元为右端节点的集中质量得到,如下:
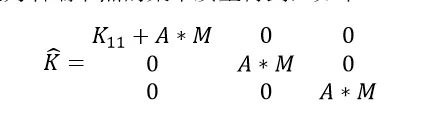

在第一个增量步,方程就变为:
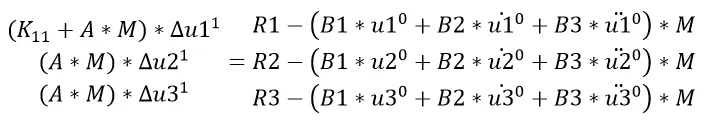

由于R只有Y方向恒值,初始位置时位移、速度都是0,但Y方向存在加速度,显然,上述三个方程变为:
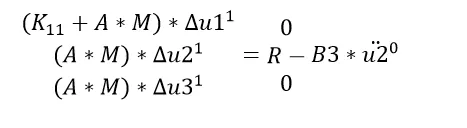

U1、U2、U3没有耦合项,可以直接解耦,分别得到三个方程。
由第一个和第三个方程可得位移U1和U3在第一个增量步结束时=0。第二个方程可得在第一个增量步结束时的位移是R/(A*M),将Newmark的梯形算法的A带入后得到:
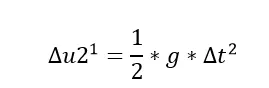

这个公式显然和我们熟知的位移和加速度的关系式完全一致。
在0.1s,得到位移U2=-4.9,和Abaqus完全一致。
其它增量步类似,我们就不再累述,最终我们可以得到一个位移U2随时间的变化曲线如下:
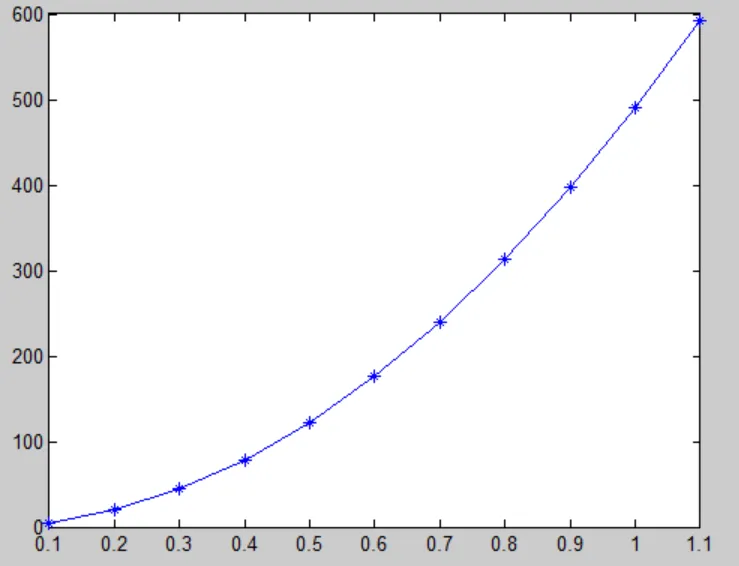

显然,都是正值,且不会往回摆动,这与实际单摆是不一致的,这将在后面章节讲到非线性瞬态动力学的问题时修正。
如果觉得上面的文字太复杂,也可以看一下视频的简要讲解,包括基于线性瞬态动力学理论和算例的操作验证,地址如下:
https://www.jishulink.com/college/video/c12884
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删