产品
本系列文章研究成熟的有限元理论基础及在商用有限元软件的实现方式，通过
1） 基础理论
2） 商软操作
3） 自编程序
三者结合的方式将复杂繁琐的结构有限元理论通过简单直观的方式展现出来，同时深层次的学习有限元理论和商业软件的内部实现原理。
有限元的理论发展了几十年已经相当成熟，商用有限元软件同样也是采用这些成熟的有限元理论，只是在实际应用过程中，商用CAE软件在传统的理论基础上会做相应的修正以解决工程中遇到的不同问题，且各家软件的修正方法都不一样，每个主流商用软件手册中都会注明各个单元的理论采用了哪种理论公式，但都只是提一下用什么方法修正，很多没有具体的实现公式。商用软件对外就是一个黑盒子，除了开发人员，使用人员只能在黑盒子外猜测内部实现方式。
一方面我们查阅各个主流商用软件的理论手册并通过进行大量的资料查阅猜测内部修正方法，另一方面我们自己编程实现结构有限元求解器，通过自研求解器和商软的结果比较来验证我们的猜测，如同管中窥豹一般来研究的修正方法，从而猜测商用有限元软件的内部计算方法。我们关注CAE中的结构有限元，所以主要选择了商用结构有限元软件中文档相对较完备的Abaqus来研究内部实现方式，同时对某些问题也会涉及其它的Nastran/Ansys等商软。为了理解方便有很多问题在数学上其实并不严谨，同时由于水平有限可能有许多的理论错误，欢迎交流讨论，也期待有更多的合作机会。
==非线性瞬态动力学==
在系列文章第三十三篇时，我们讲了线性瞬态动力学的原理，瞬态分析有线性和非线性之分，如果系统有材料、大变形、边界等非线性效应，那么就是非线性瞬态分析，而瞬态分析往往都有物体的大转动大变形问题，也会涉及材料的损伤破坏、物体的撞击接触等，譬如冲击爆炸就是典型的强非线性瞬态动力学的过程，所以在实际工程中的瞬态分析都是以非线性为主。本章我们介绍一下非线性瞬态动力学的求解公式，并以上次线性瞬态动力学中的单摆例子来说明非线性瞬态动力学在有限元软件中的内部实现原理。
瞬态动力学的运动方程包括了质量阵M相关的惯性力项和阻尼阵C相关的阻尼力项，如下：
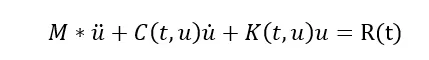
一般质量矩阵与时间和位移无关，而K和C如果和位移和时间相关，那么就是非线性瞬态问题。为简单起见，我们不考虑阻尼项。得到如下表达式：
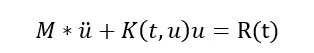
和线性瞬态动力学类似，在理论上当前时刻的加速度就应该只和当前时刻的位移相关了，但计算的数值解把时刻分成了多个，方程如下：
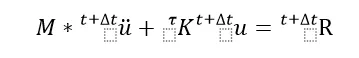
其中
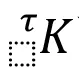
可以取当前时间步的初始时刻的刚度，那么就是修正的牛顿迭代方法，如果取结束时刻的刚度，就是完全牛顿迭代方法。
而加速度一定是要通过起码两个时刻才能计算出来的，取前时刻还是后时刻的位移来决定加速度就有隐式和显式之分，任何一种分析理论上都可以得到正确解，只不过显式不用求刚度，隐式需要求解刚度阵，而通过刚度的解释可以更容易理解Abaqus内部的实现原理，在本章中，我们选用隐式非线性瞬态分析。在隐式方法中，将时间离散，加速度表示为位移的表达式后，得到下方的公式
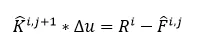
这个就是标准的newton增量迭代法的公式，其中K和F在静力学的增量迭代法中表示切线刚度阵和内力，只不过这边需要加上M项：
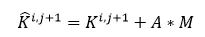
其中A依然是只与时间增量步相关的量，对不同的隐式算法A的值不同，譬如对最简单的Newmark方法中的梯形隐式算法，加速度在增量步内线性变化，譬如下方红线是在输入的载荷转换为加速度的值，但计算中没法处理连续的曲线，所以Abaqus或者iSolver中实际上只会认为增量步内加速度时线性变化的：
此时得到的修正刚度为：
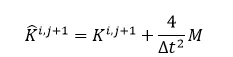
而F与上一迭代的位移、速度、加速度相关，可以表示为：
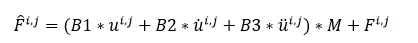
显然当时间增量步固定时，此时的K也是随增量步和迭代步变化的值，显然该方程在每个时间步长内都只能通过迭代。因为有迭代，所以F也无法约去右侧纯的应力导致的内力项。
最后我们再讨论一下稳定时间步的问题，在系列文章13：显式和隐式的区别和25：显式分析的稳定时间增量中，我们都讨论过，CAE求解方法一般有两种，分别为显式（Explicit）和隐式（Implicit）。显式分析时间步长不稳定的，就是增量步长也不能过大，一般不超过模型最小自由振荡周期的1/10，否则容易导致计算结果发散。
那么隐式就一定是时间步长稳定的吗？如果是稳定的，那为何大家用Abaqus的Standard隐式求解器的时候处理后屈曲、材料软化或者冲击爆炸这种问题经常会碰到很难收敛的问题呢？
大家使用软件的经验只能说明隐式算法也不一定稳定的。Abaqus的Standard求解器都是把有限元的问题最终转化为增量迭代法求解数值问题的，时间步长是否稳定就看增量迭代法求解的过程。
1）对于线性瞬态动力学，无需迭代，一次迭代就能求出问题解，且是正确解，自然是稳定的。
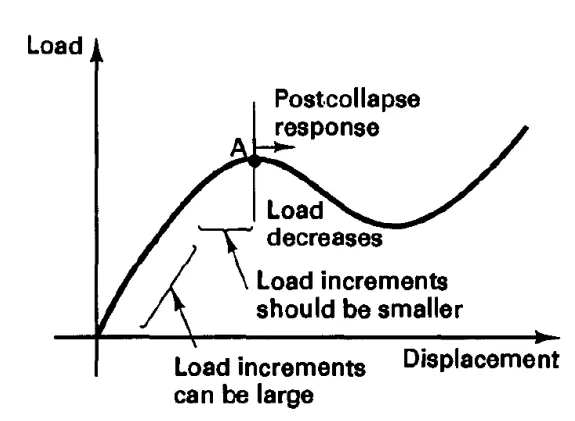
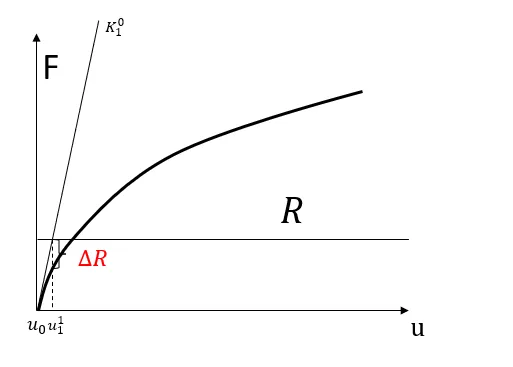
2）对于非线性瞬态动力学，需要多次迭代完成，只要迭代求解曲线问题的算法，就可能存在无法收敛的问题，譬如坍塌问题，也就是力一开始随着位移上升，在某个极值点时力随着位移下降，曲线有下面类似的马鞍点。譬如下面的A点，在接近接近极值点A时，此时斜率非常小设为，如果第一个t=0时刻的K是K0的话，此时斜率可以认为a*K0，a非常小。
本章我们依然采用线性瞬态动力学中的单摆例子
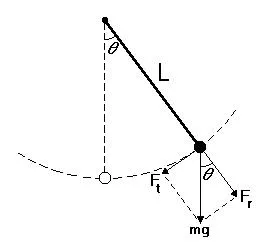
这次我们在Abaqus中将几何非线性打开，此时软件将按非线性瞬态动力学进行分析：
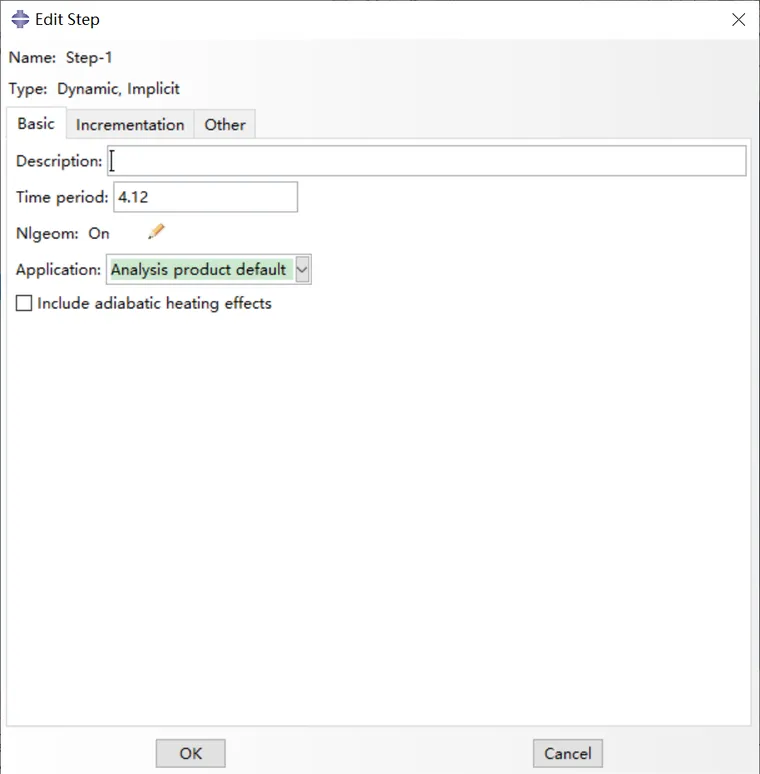
0.5s时刻的位移（左侧是Abaqus，右侧是iSolver）
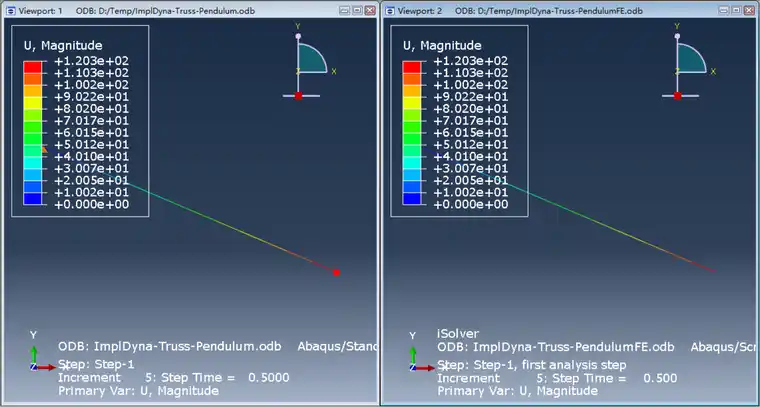
1s时刻的位移（左侧是Abaqus，右侧是iSolver）
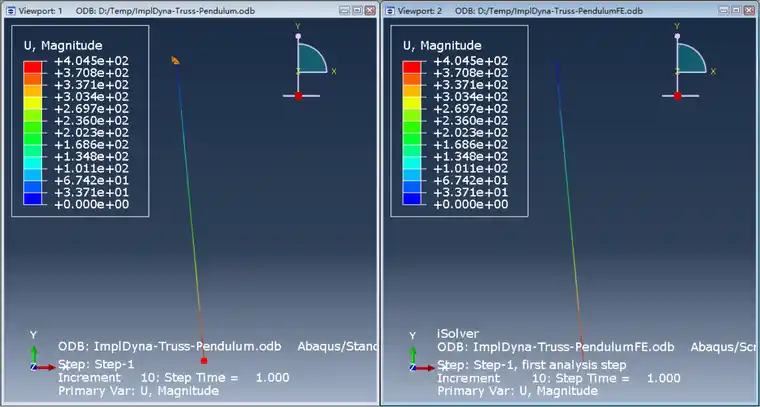
1.5s时刻的位移（左侧是Abaqus，右侧是iSolver）
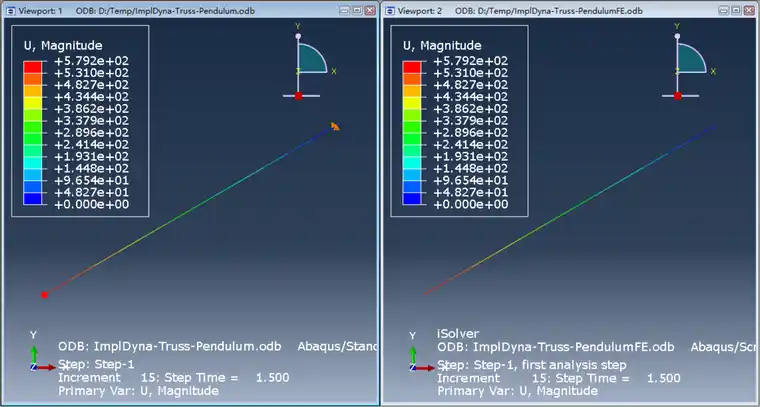
4.12s时刻的位移（左侧是Abaqus，右侧是iSolver）
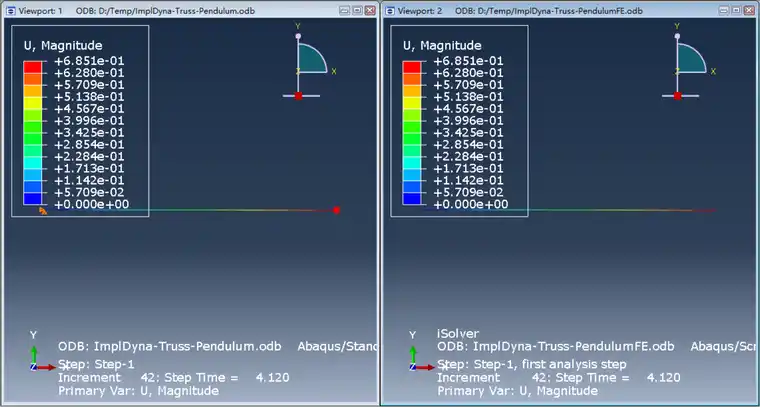
整个运动过程动画如下（左侧是Abaqus，右侧是iSolver）
查看右端节点位移曲线如下：
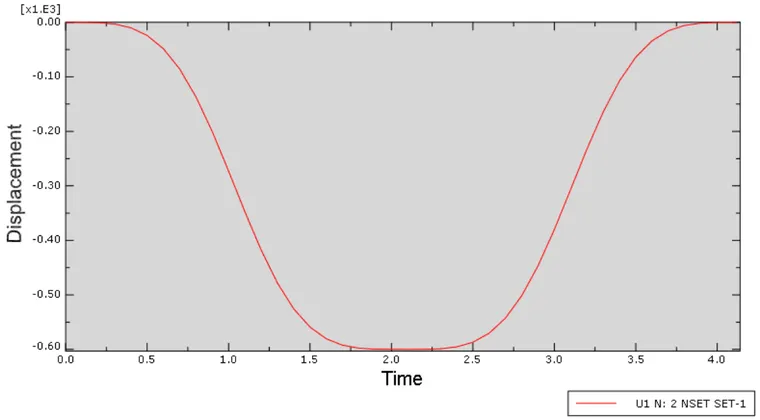
显然，单摆随着时间在纸面内左右摆动，和真实情况一致，且可以发现一个周期和理论值4.12s吻合。
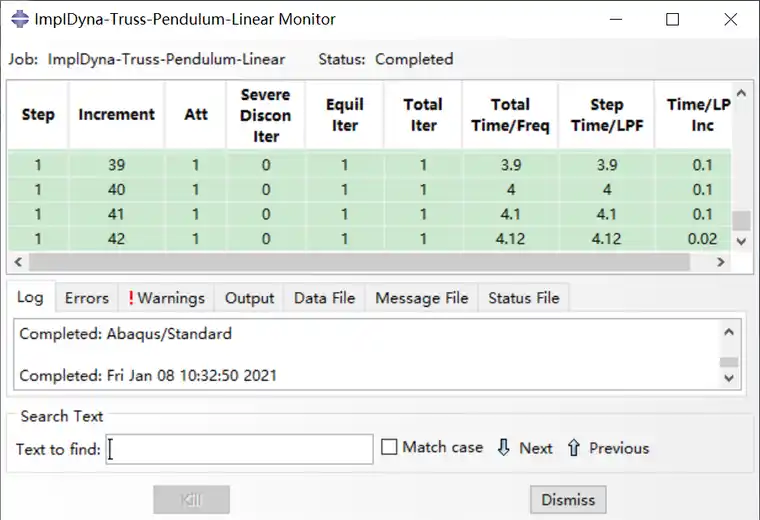
在系列文章32章线性瞬态动力学中，我们可以发现如果几何非线性没打开，单摆的迭代iter在Monitor中都是1，也就是没有迭代：
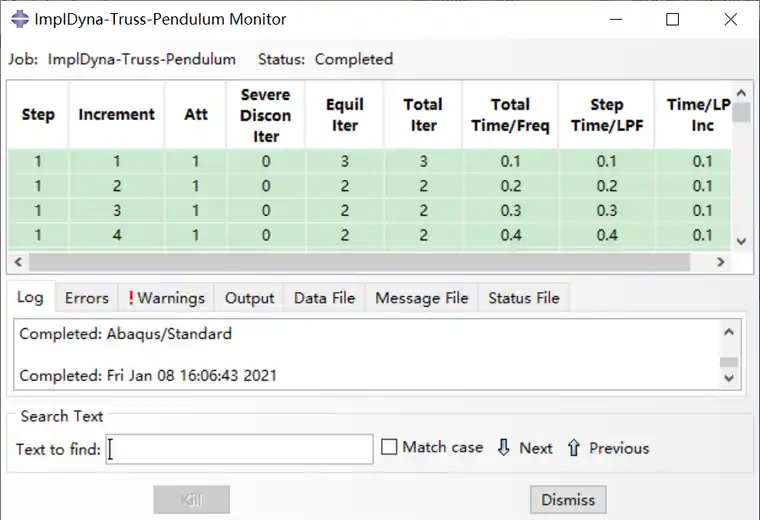
本章中，将几何非线性打开后，可以发现Monitor中，iter已经不再是1了，说明了非线性瞬态动力学需要迭代才能执行。
K在第一个增量步第一个迭代步时，是水平方向初始长度的刚度：
在第一个增量步，方程就变为：
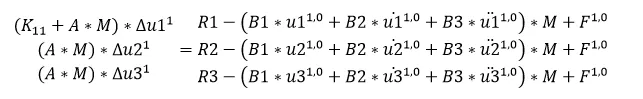
初始条件下：
1）R只有Y方向恒值
2）初始位置时位移、速度都是0，但Y方向存在加速度
3）
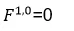
显然，上述三个方程变为：
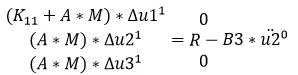
U1、U2、U3没有耦合项，可以直接解耦，分别得到三个方程。
由第一个和第三个方程可得位移U1和U3在第一个增量步结束时=0。在程序中强制设置迭代步=1，在0.1s时刻可得U1=0，和上述理论一致：
第二个方程可得在第一个增量步结束时的位移是R/(A*M)，将Newmark的梯形算法的A带入后得到：
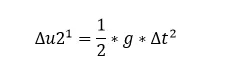
这个公式显然和我们熟知的位移和加速度的关系式完全一致。
在0.1s，得到位移U2=-4.9，在程序中强制设置迭代步=1，在0.1s时刻可得U1=0，和上述理论一致：
在第一次迭代后，程序将判断三个方向的不平衡力情况
此时的F要用此刻的位移、速度、加速度等构型计算，在这个时刻，由于单摆已经摆动了一个角度，因此，F计算出的内力必然和KU已经不一致了，导致也和外力R不一致，只能进入下一次迭代。
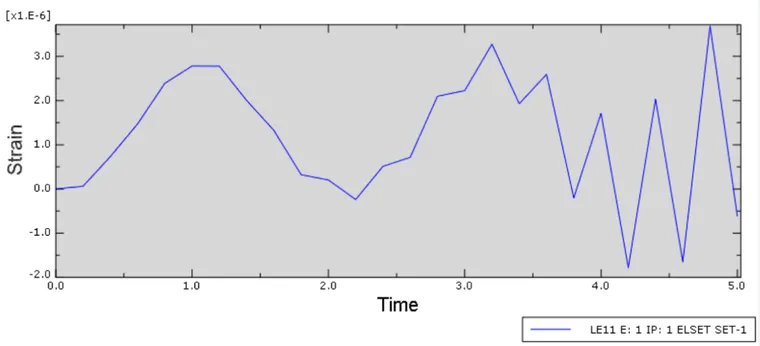
在前面理论中，我们也提到了，只要是迭代，就有不收敛的可能性，在该例中，我们将步长设为0.2s，此时得到的位移曲线如下：
位移看起来很正常，但我们要是查看杆中的应变曲线时，可以发现应变在半个周期内还是正常的，但在半个周期后面明显发散了。
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
