1 概述
在CAE领域,从学校、实验室的自研算法到实现真正的商业化软件是一条无比漫长的道路。我们不研究有限元的新方法、新理论,只是研究商用有限元软件的实现方式。有限元的理论发展了几十年已经相当成熟,商用有限元软件同样也是采用这些成熟的有限元理论,只是在实际应用过程中,商用软件在这些传统的理论基础上会做相应的修正以解决工程中遇到的不同问题,且各家软件的修正方法都不一样,每个主流商用软件手册中都会注明各个单元的理论采用了哪种理论公式,但都只是提一下用什么方法修正,很多没有具体的实现公式。

一方面我们查阅Abaqus软件手册得到修正方法的说明,另一方面我们自己编程实现简单的结构有限元求解器,通过自研求解器和Abaqus的结果比较结合理论手册如同管中窥豹一般来研究Abaqus的修正方法,从而猜测商用有限元软件的内部计算方法。在研究的同时,准备将自己的研究成果记录下来写成一个系列文章,希望对那些不仅仅满足使用软件,而想了解软件内部实现方法甚至是做自己的软件的朋友有些帮助。
2 第四篇:非线性问题的求解
随着分析对象越来越复杂,有限元软件从线性分析向非线性分析(如材料为非线性、几何大变形导致的非线性、接触行为引起的边界条件非线性等)发展,Abaqus的强大主要就在于能解决各种工程上的非线性问题。由于非线性理论和编程实现的困难性,研究起来也相对困难,只能一步步来,我们在本文中首先研究各种非线性都会遇到的求解问题和Abaqus的内部实现方式。很多人做非线性编程结果正确性验证由于不知道商软的内部实现方式,采用小模型或者有理论解的模型对比理论结果和商软最终的迭代结果,可能最终的结果差不多,但这种方法很容易就忽略了非线性中细节问题,如果进一步对比迭代过程,就会发现迭代效率和精度和商软相比差距较大,这种效率和精度当遇到复杂工程问题时就尤为重要了。我们试图通过自编程序和Abaqus非线性的每个迭代步的中间输出量进行对比,最终结合帮助文档猜测Abaqus软件非线性迭代的内部实现方法。

在非线性分析过程中,无论哪一类非线性问题,经过有限元离散后,都可以转化为求解一个非线性方程组,对一个简单的一维问题,最终得到的非线性平衡方程如下
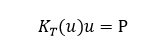

已知P,求u。如果是线性问题,那么直接用
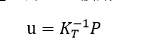

如果是非线性问题,K与u相关,那么就不能简单的用上面公式了。非线性问题求解有多种方法主要分为以下几类:增量法、迭代法、增量迭代法和弧长法,下面将具体讲一下这几类方法。
增量法的基本思想就是将施加外载荷的过程分割为若干个增量步,每一步只施加一个比较小的载荷增量,总载荷引起的位移就是所有增量步位移增量的累加。
对于每一个载荷增量 ,平衡方程
,平衡方程
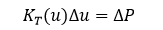

在一个增量步内,我们可以把位移和载荷的变化看作是线性变化的过程。只要这些增量步取得够小,最后求解的位移结果与实际值之间的差异将在容许的误差范围内。
理论上讲,如果没有极值点,也就是一个P和u一一对应,那么增量法总能求得真实解。但实际工程应用情况中,增量步的步长不可能无限小且增量步位移增量的累积误差可能非常大造成最终结果偏差很大。同时,在位移-载荷曲线的极值点处,切线刚度矩阵为零,位移方程无解。


直接迭代法取迭代方程为

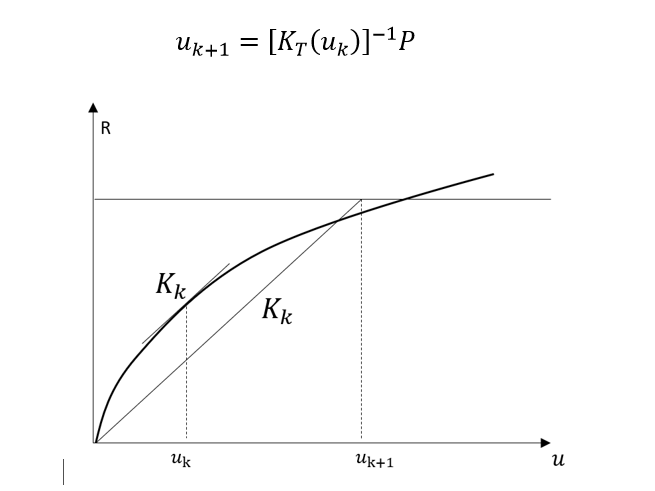

迭代方程
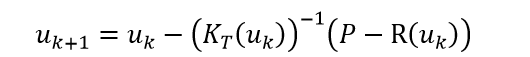

详细推导可见附录。K的值和上面的直接法是一样的,但最大区别是第一次迭代的u作为下一次的初始点。
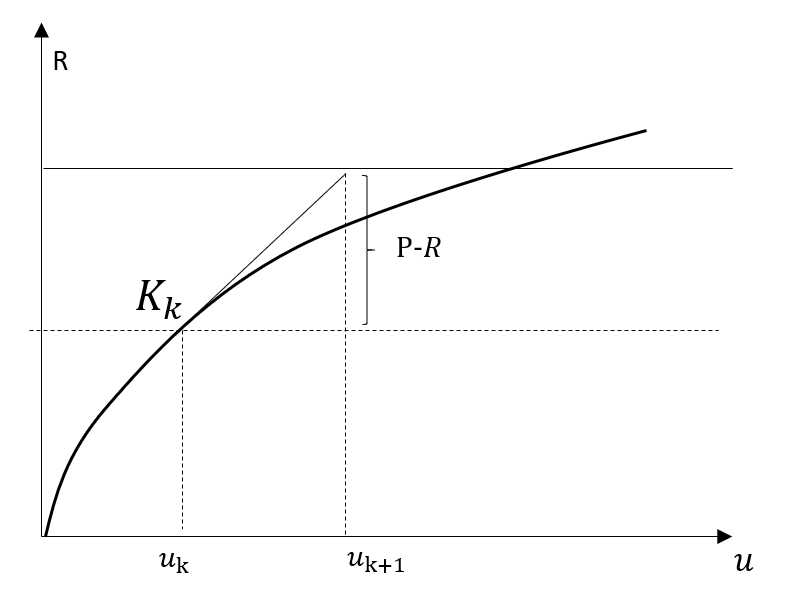
如果非线性曲线比较平缓,那么在New-Raphson迭代过程中迭代步的切线刚度矩阵可以近似为上几个或者第一个迭代步的,即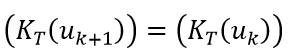
 。这样可以只在第一个迭代步计算一次K,提高每个迭代步的计算速度,但由于一般情况下
。这样可以只在第一个迭代步计算一次K,提高每个迭代步的计算速度,但由于一般情况下
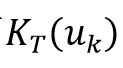
 的变化较大,所以会降低收敛速度。
的变化较大,所以会降低收敛速度。
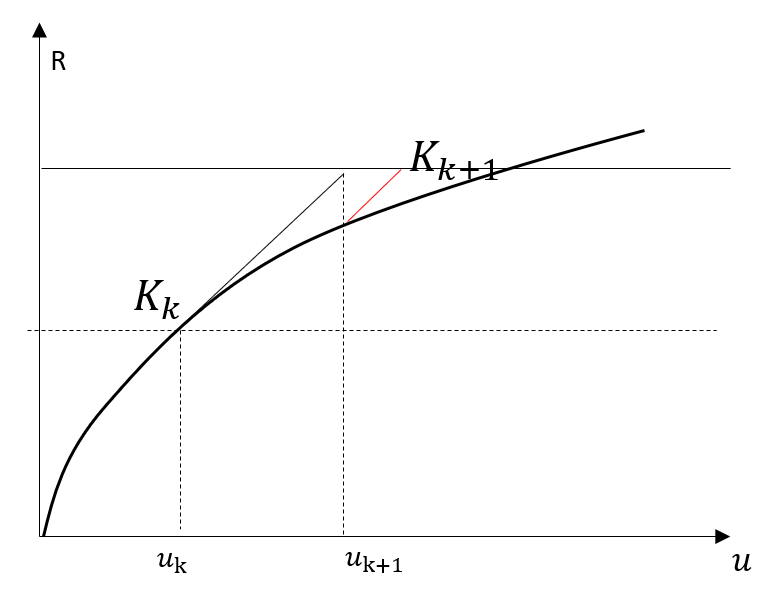

其实就是Abaqus非线性Step设置中的Quasi-Newton方法,在Abaqus做非线性可以在Newton方法和Quasi-Newton二选一。这里不做更多说明。
一般情况增量法可以保证求解过程的收敛性但收敛速度较慢,而Newton-Raphson法收敛速度较慢但收敛性没有保证,所以混合法结合了增量法和Newton-Raphson法来求解非线性问题。混合法首先将外载荷分成若干个增量步,在每个增量步内采用Newton-Raphson法迭代求解,在增量步内求解完成后继续求解下一个增量步,最后将所有增量步累加起来即得到结果。
常见的收敛判据有分为两种,失衡力准则、位移准则




Abaqus的非线性中上面说的三种迭代都涉及,其中General Static分析步采用Newton或者Quasi-Newton方法,而Static, Riks分析步采用Riks弧长法。我们现在只聚焦到General Static的Newton方法。
详见Abaqus Theory Manual v6.12: 2.2.1 Nonlinear solution methods in Abaqus/Standard
Abaqus/Standard generally uses Newton's method as a numerical technique for solving the nonlinear equilibrium equations. The motivation for this choice is primarily the convergence rate obtained by using Newton's method compared to the convergence rates exhibited by alternate methods (usually modified Newton or quasi-Newton methods) for the types of nonlinear problems most often studied with Abaqus.
Example 1:非线性弹簧例子(详见附件Test30 SpringNonLinear.cae Model-NonLinearSpringY4)
本篇采用定义应力应变的关系来模拟非线性的变化过程。
创建一根线弹簧,左端取固支约束,右端X方向拉力。
参数如下:
尺寸:X方向长度L=1。
载荷幅值:R=5000


Abaqus中非线性弹簧设置如下:在Interact模块的Connector Section中,选择类型为Basic,平移为Axis,旋转为None,在Behavior Options中添加Elasticity,定义为Nolinear,在Data表中添加应力应变数据。
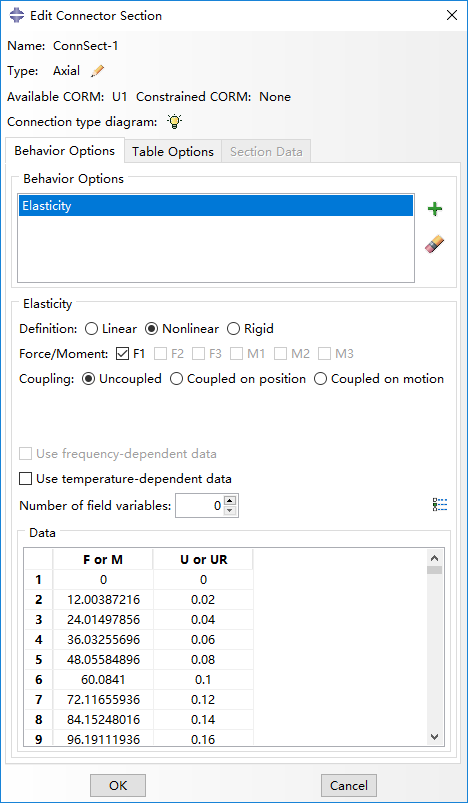

输入的应变-应力曲线如下图所示:
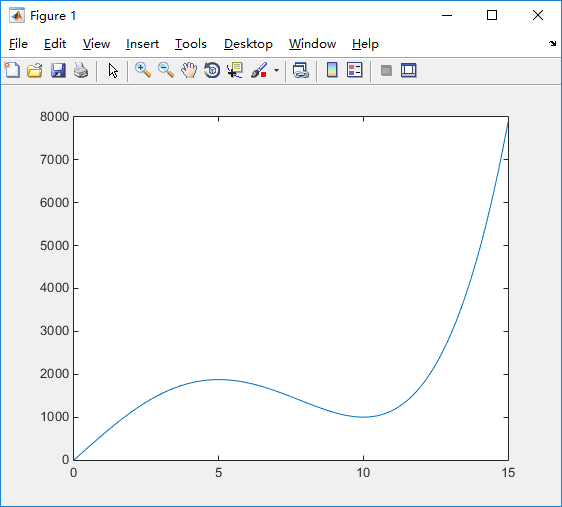

Step选择Static,Generic,Initial Increment Size如果是默认的话就是1,也就是全量,我们这里改为0.1,其他默认。
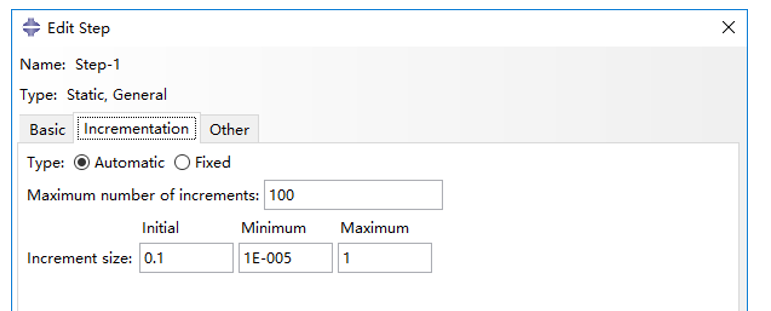

在Other中默认使用Newton-Raphson方法。
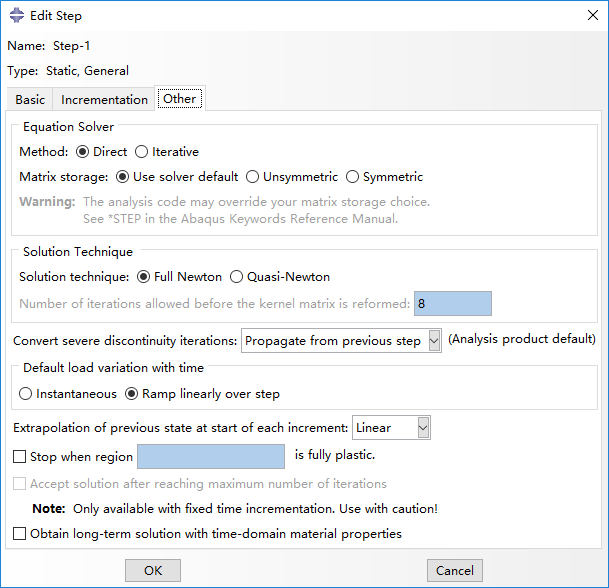

提交job计算,计算完成后打开对应的*.msg文件和*.sta文件查看我们需要的信息。
Abaqus的Genera Static分析步采用增量迭代法来求解非线性分析问题,默认采用结合增量法和Newton-Raphson法的混合法。
下面,笔者将参照这sta文件和msg文件来讲此算例中Abaqus非线性问题的求解步骤。





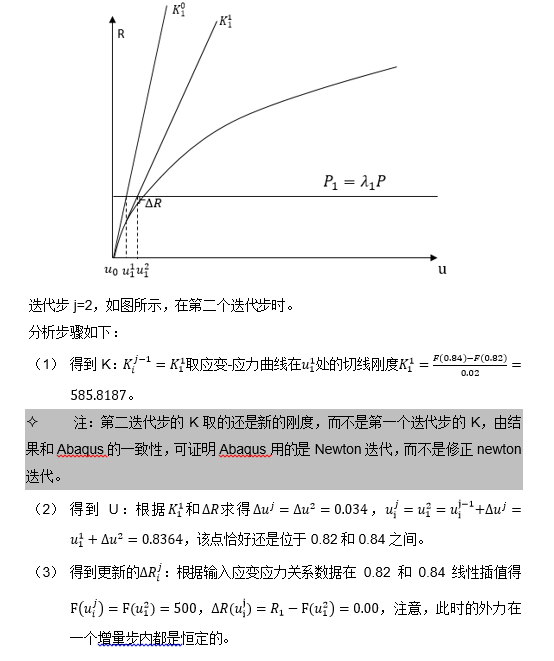




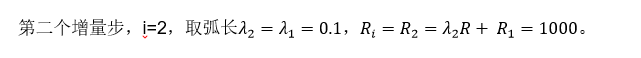

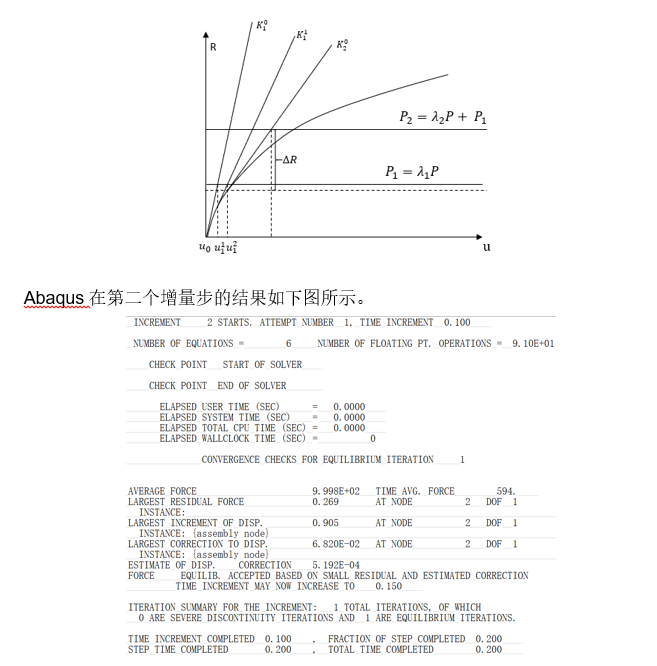


迭代求解过程同上。
最终应力和应变的计算结果如下图所示。


最终计算的增量和每个增量步的迭代次数如下图所示。
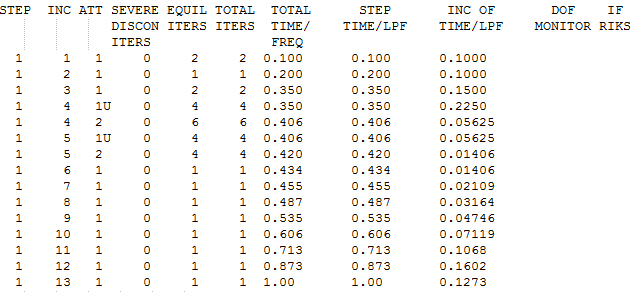

由上图可知,Abaqus在分别在进行第一次计算第四个增量步和第一次计算第五个增量步时,因为求解不收敛,所以增量步大小减为原来的0.25。
本文简单介绍了非线性问题的几种常用求解方法,并给出了在结构有限元非线性求解时遵循的收敛准则。同时,给出了一个非线性弹簧静力分析的例子(详见附件SpringNonLinear.cae),并通过这个例子描述了Abaqus采用增量迭代法求解非线性问题的过程。
各种求解方法的优缺点如下:
| 方法 | 优点 | 缺点 |
| 增量法 | 收敛性较好 | 收敛效率低,累积误差较大,某些时候会出现增量步过小而无法进行实际计算的问题 |
| 迭代法 | 收敛效率较高 | 收敛性较差 |
| 增量迭代法 | 收敛性比迭代法好,收敛效率高 | 不能根本上解决迭代法收敛性的问题 |
| 弧长法 | 收敛性好,计算稳定性高 | 增量步过多,求解效率低 |
如果有任何其它疑问,欢迎联系我们:
snowwave02 From www.jishulink.com
email: snowwave02@qq.com
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删