基于多点位移控制增量的网壳结构稳定性分析技术

（一）背景及基础理论      

网壳结构是一种重要的空间结构形式，对于单层网壳结构来说，稳定性问题是其结构设计中的重要问题。对于网壳结构稳定性问题来说，考虑材料-几何双重非线性下的非线性屈曲的求解方法一直是计算力学中的具有挑战性的研究方向。本质上，非线性屈曲实际上要求解的是一个非线性静力问题，在有限元中最终转化为非线性方程组的求解，目前常见的非线性方程组的求解方法有牛顿迭代法、拟牛顿迭代法、增量法、增量迭代法和弧长法等。在abaqus中，如果采用static，general类型的step，则软件采用增量迭代法进行计算，具体是将荷载/位移分为多个增量步加载，而每一个增量步内又采用牛顿迭代法进行求解。

对于单层网壳结构来说，在abaqus中，其计算非线性屈曲主要采用两种方法：增量迭代法和弧长法。增量迭代法又分荷载增量迭代和位移增量迭代。对于单层网壳，由于通常情况下其所受的外荷载已知而在外荷载的位移未知，因此实际工程中事实上很难采用位移增量迭代，而对于荷载增量迭代，其具体过程如图一所示：

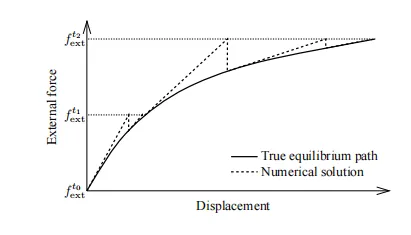
图一 基于荷载增量的增量迭代法

基于荷载增量迭代的具体求解过程可知，如果荷载-位移曲线存在下降段，则荷载增量迭代实际上在曲线接近峰值时由于刚度接近0而不收敛，难以继续求解，具体过程如图二所示：

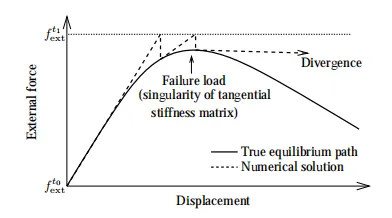
图二 基于荷载增量的不收敛示意

目前应对此缺陷的方法是采用弧长法，其具体过程如图三。由于弧长法以荷载和位移形成的弧长作为增量，因此即使是面对有下降段的非线性屈曲分析，其也能求解。然而实际上，即使是采用弧长法，对于复杂结构，即使是采用弧长法，在面对平衡路径跳跃或者突变时，仍可能存在不收敛。另外，在abaqus中，通常情况下在设置了弧长法的static，riks类型的step后，后面无法继续施加其他类型的step，这也导致了例如需要考虑屈曲后的动力分析无法直接进行。

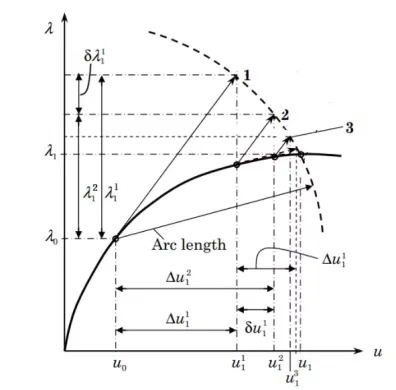
图三 弧长法求解示意

实际上，对于有下降段的平衡路径来说，位移增量迭代实际上有天然的优势，在位移增量永远为正值的条件下，其几乎能够能够完美跟踪下降段的平衡路径，目前不被采用主要是其无法保证加载过程中荷载比例关系与结构实际所受外荷载一致。

本研究基于abaqus中的约束方程，实现位移增量迭代的同时保证荷载比例与要施加的荷载比例一致，从而实现网壳非线性屈曲的更优化求解。具体理论如下：

对于一个网壳结构，假设其n个节点所受外荷载分别为F1，F2,...,Fn。要使网壳在加载过程中始终保持该比例关系，则只需设置第n+1个节点，并且对所有节点施加以下约束方程：

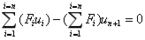                                                                                                                                                   （1）
   

（二）计算条件

上述理论由加州伯克利大学的黄羽立提出，本研究基于该理论对K6型网壳结构的非线性屈曲进行分析，具体结构如下：

设计参数：网壳矢高，跨度32m，矢高4.29m，网壳杆件截面采用80x8，材料为Q235钢，材料属性采用理想弹塑性。

边界条件：网壳底边一圈铰接。

单元类型：B32，每个单元长度约0.5m，共有节点数2437，单元数目1266

荷载：采用位移加载：本研究基于多点位移控制增量，为简化约束方程的定义，假设下图中点1荷载为Z向-4e5N，点2为-3e5N,点3为-2e5N，点4为1e5N，以该荷载比例为基础定义具体的约束方程，然后仅需要在对应的约束方程的控制参考点上施加位移边界条件而不需要施加荷载，参考点处的位移设置为-0.5m。

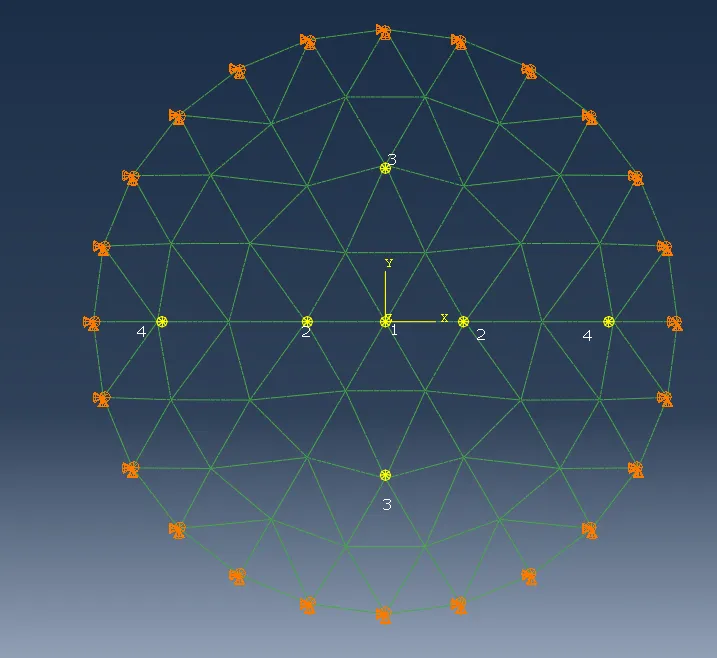
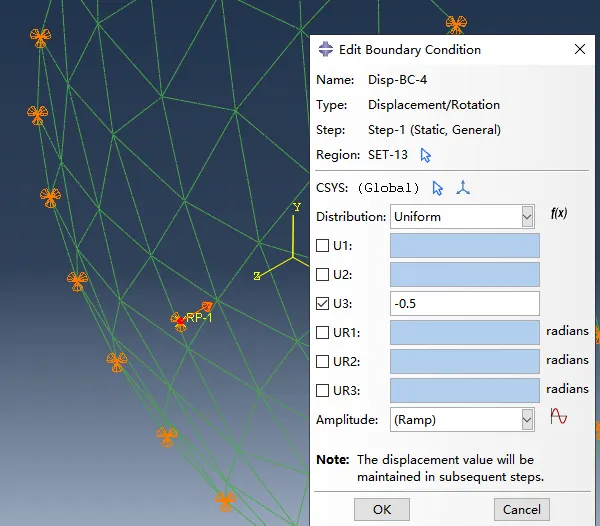
采用约束方程，对施加荷载点进行约束，设置主约束XP点，其位置为点1往z轴移动1m。最终依据式（1）定义的约束方程如下：

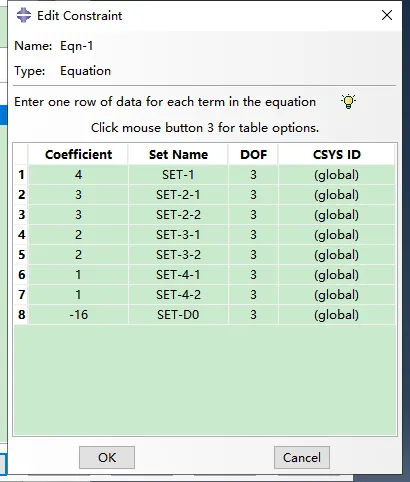
为便于对比，采用同样模型进行弧长法计算，仅仅是取消约束方程，而代替以实际的荷载施加，并用static，riks类型的step进行同样的计算。

（三）计算结果：

网壳的最终屈曲变形形状如下图：

荷载位移曲线：

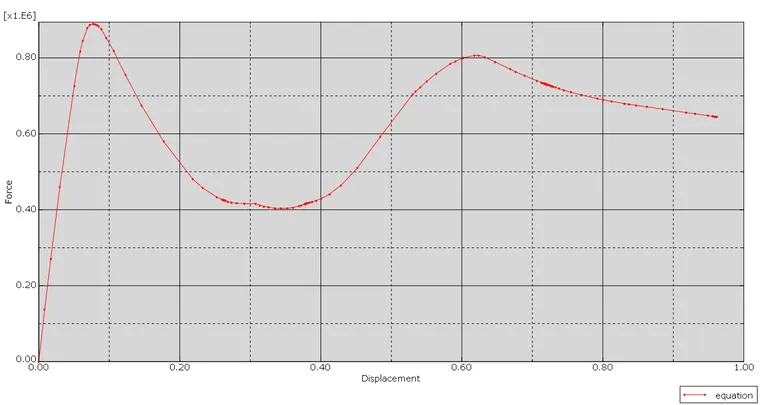
从上述结果可以看出，结构在此种荷载模式下的最大基底反力约为0.9e6N。同样对该结构，采用常规的弧长法（static，riks）进行分析，与采用多点位移控制的曲线对比如下图：  

从计算结果可以看出，采用本研究的多点位移控制和弧长法计算结果基本一致，表明了采用约束方程实现多点位移控制的非线性屈曲的准确性。

计算环境与计算时长：

计算环境：AMD3900X 12核CPU，内存16G

计算时采用USE multiprocessors设为12，multiprocessing model采用MPI

计算时长：多点位移控制技术和采用弧长法计算时长均为200s左右。

结论：

采用约束方程+位移加载可以有效地实现特定荷载分布下的单层网壳结构非线性屈曲分析，从而改善荷载增量法无法得到下降段的缺陷，是一种堪比弧长法的高效静力非线性计算方法。同时，该方法相对于弧长法来说，其可以在该step后添加其他step，从而实现网壳结构屈曲后继续承载下的结构分析，是一种高效的计算方法。另外，在同样是静力非线性分析的pushover分析中，也可以采用此方法实现pushover震后承载力分析。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删