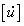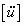Abaqus动力学分析入门指南

结构动力分析与静力分析是结构力学分析的两大基本类型，两者的最大区别在于是否考虑惯性力对结构的影响。一般地，如果结构体系的自振频率和荷载激励频率相差很大，则激起的结构振动将会十分缓慢，所引起的惯性力可以忽略不计。

基本方程

式中，[M] 为结构的质量矩阵，[C] 为结构的阻尼矩阵，[K] 为结构的刚度矩阵，[u] 为节点位移列阵，

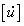
为节点速度列阵，

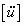
为节点加速度列阵，{F} 为节点载荷列阵。

动力学问题分类

按照分析内容的不同，动力学问题可以分为以下几类：

• 模态分析 (frequency)：模态分析用于确定结构在自由振动下的动力特性，即结构的自振频率和振型。模态分析是进行其他动力学分析的基础，一般只考虑线性材料和线性行为。当然，在abaqus也可以进行结构在非线性行为后的模态分析。
• 稳态动力学分析，即谐响应分析 (steady-stateddynamic)：稳态动力学分析用于确定结构在简谐荷载作用下的稳态响应，激励荷载可以是力或者位移，最终得到结构在频域内的响应。同样，稳态动力学分析仅考虑线性行为。
• 瞬态动力学分析 (dynamic)：瞬态动力学分析用于研究时域载荷作用下结构的动力响应。
• 响应谱分析 (response spectrum)：响应谱分析用于分析结构在给定的响应谱下的峰值响应，它需要将结构的模态分析结果和响应谱结合起来求解。
• 随机响应分析 (random response)：随机响应分析用于分析结构在随机载荷（用功率谱密度表示）下的动力响应，计算结果为给定可信度下的结构响应，是一个统计数值。

动力学问题计算方法

对于不同的分析类型，ABAQUS提供了多种计算方法，主要可以分为三大类：

• 直接法：对模型的动力学方程直接积分求解，计算精度高，但耗时较多；
• 模态叠加法：将模型的动力学方程在模态坐标系下进行解耦，得到一组用模态坐标表示的单自由度运动方程，然后对各个单自由度运动方程进行求解。计算精度低于直接法和子空间法，但耗时最少；
• 子空间法：将动力学方程投影到一组特征模态空间（包含足够数量的特征模态向量）进行求解，形成减缩（并不解耦）的方程组，然后进行求解。

计算精度（高—>低）：直接法>子空间法>模态叠加法

计算耗时（少—>多）：模态叠加法<子空间法<直接法

那么，对于稳态动力学分析、瞬态动力学分析、响应谱分析和随机响应分析，ABAQUS提供的具体计算方法如下：

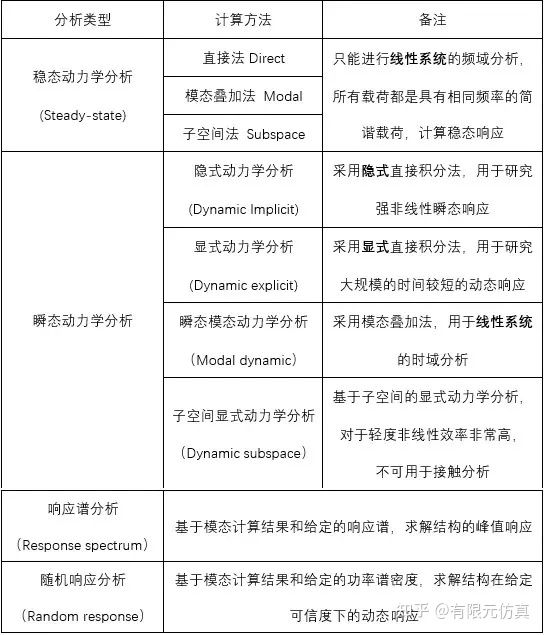
附：显式算法和隐式直接积分法的区别

• 显式算法：ABAQUS中显式算法采用的是中心差分法，对时间进行差分，无需进行迭代，因此不存在收敛性问题。但是，时间增量步一般很小，适用于分析冲击、碰撞等时间短暂的动力学问题，以及复杂的非线性问题；
• 隐式算法：ABAQUS中隐式算法采用的是Newmark法，需要迭代求解非线性方程组，因此存在收敛性问题。但是，可以设置较大的时间增量步。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删