Abaqus材料属性定义：非线性粘弹性与并行流变模型

1. 理论模型

并行流变模型如下图：

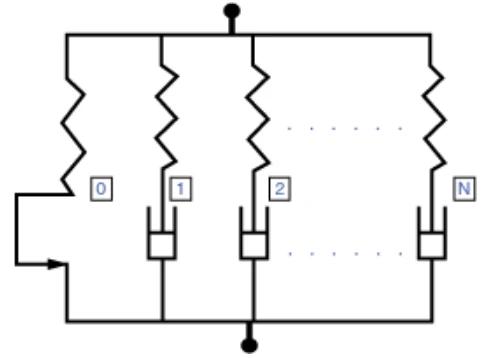
   图1 具有多个并行网络的非线性粘弹-弹塑性模型。
 

其中，粘弹性网络的数目N可以是任意的；然而，最多只能有一个平衡网络（图1中的network 0），且这个平衡网络响应可以是纯弹性的，也可以是弹塑性的，也可包括mullinus效应来预测材料的软化。平衡网络的定义是可选的，如果没有定义，则材料中的应力将随时间完全松弛。

该模型可用于预测材料在有限应变作用下的复杂行为，这是其他Abaqus模型无法准确模拟的。图2中描述了这种复杂行为的一个例子，它显示了三种不同应变水平的归一化应力松弛曲线。这种行为可以使用图3所示的非线性粘弹性模型精确建模，注意由于不同应变下归一化后不一致，因此是不能用线性粘弹性模型来描述的。

   图2 三种不同应变水平的归一化应力松弛曲线
 

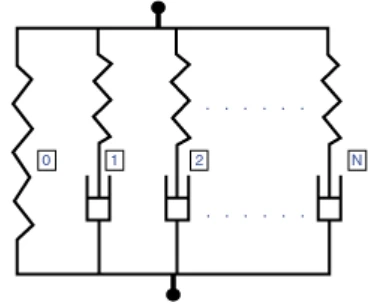
   图3 具有多个并行网络的非线性粘弹性模型
 

弹性行为（平衡网络只包含弹性行为时，如图3中的network 0）：

如果平衡网络只包含弹性行为时，需使用超弹性材料模型来指定。可以使用Abaqus中提供的任何超弹性模型。所有网络都使用相同的超弹性材料定义，通过每个网络的刚度比进行缩放。因此，模型只需要一个超弹性材料定义以及每个网络的刚度比。同时，弹性响应可以通过定义瞬时响应或长期响应来指定。

平衡网络行为（平衡网络可为弹塑性或可同时包含Mullinus效应时，如图1中的network 0）：

除了上述的弹性响应外，平衡网络的响应还可以包括塑性和Mullins效应来预测材料的软化。

如果使用各向同性硬化定义塑性响应，则平衡网络中的响应等效于Abaqus中类橡胶材料的永久变形模型（在后续的专利更新）。

在Abaqus/Standard中，除了各向同性塑性硬化外，还可以指定具有多个背应力的非线性运动硬化模型。非线性运动硬化模型是对金属塑性模型（在后续的专利更新）的推广。不同之处在于，在目前的公式中，柯西应力被基尔霍夫应力所取代。

粘性行为（图1或图3中的Networks 1...N）：

必须定义每个粘弹性网络的粘性行为。

假设变形梯度由下式计算：

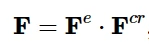
   变形梯度
 

即变形梯度=变形梯度的弹性部分*变形梯度的蠕变部分；

在该模型中，蠕变势由下式计算：

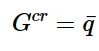
   蠕变势
 

其中q- 为等效偏柯西应力。那么流动法则由下式计算：

   流动法则
 

其中，Dcr是速度梯度的对称部分，ε¯˙cr 为等效蠕变应变率，σ¯ 为偏柯西应力，τ¯ 为偏基尔霍夫应力，且满足：

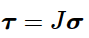
和

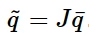
其中，J是变形梯度F的行列式。

等效蠕变应变率ε¯˙cr 可以由以下多种模型定义：

① Power law model：

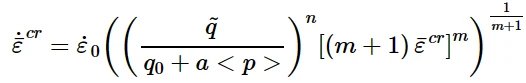
② Power-law strain hardening model：

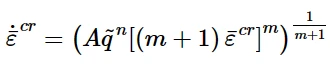
③ Hyperbolic-sine law model：

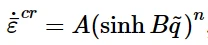
④ Bergstrom-Boyce model：

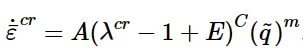
⑤ User-defined model in Abaqus/Standard：

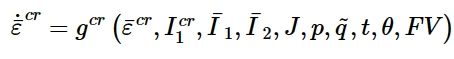
2. Abaqus定义

只能通过输入文件指定。需要指定每个粘弹性网络的标识符、刚度比和蠕变法则来定义非线性粘弹性响应。

2.1 定义网络的标识符

材料模型中的每个粘弹性网络必须分配一个唯一的网络标识符或网络id。网络标识符必须是以1开头的连续整数。它们被指定的顺序并不重要。

2.2 定义刚度比

每个网络对材料整体响应的贡献由刚度比 r 的值决定，用于衡量网络材料的弹性响应。粘弹性网络的刚度比之和必须小于等于1。如果和等于1，则说明没有建立纯弹性平衡网络。如果总和小于1，则说明创建了具有刚度比 r0 的平衡网络：

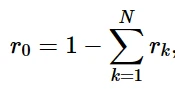
   N为粘弹性网络个数，rk为网络k的刚度比
 

可以指定刚度比在分析期间保持不变，或作为温度和预定义的场变量的函数而变化：

2.3 定义蠕变法则：均通过输入文件定义。

① Power law creep model；

② Power-law strain hardening creep model；

③ Hyperbolic-sine creep model；

④ Bergstrom-Boyce model；

⑤ User-defined creep model；

注意，根据单位的选择，应变幂律、双曲正弦和Bergstrom-Boyce模型中的参数A值对于典型的蠕变应变率可能非常小。如果A小于10的−27次方，则数值困难会导致材料计算错误;因此，在计算蠕变应变增量时，应采用不同的单位制来避免这种困难。

3. 单元和输出

在Abaqus/Standard中，材料在所有应力/位移过程类型中都是激活的。然而，蠕变效应只在准静态分析，热力耦合分析，直接积分隐式动力分析、稳态传递分析情况下考虑。如果材料用于稳态传递分析，它不能包括塑性。在其他应力/位移过程中，状态变量的演化被抑制，蠕变应变保持不变。在Abaqus/Explicit中，蠕变效果总是处于激活状态。

除了一维单元外，并行流变模型可以使用包括力学行为(具有位移自由度的单元)的连续单元。并行流变模型还支持使用平面应力公式的单元，如固体平面应力单元、膜和壳。然而，这些单元不支持可压缩材料。如果使用平面应力单元指定可压缩材料，Abaqus将修改该材料使其不可压缩并发出提示消息。

除了Abaqus中可用的标准输出标识符外，以下变量对于非线性粘弹性材料模型具有特殊意义（当网络0假设是纯弹性网络时）：

CEEQ：总等效蠕变应变

CE：总蠕变应变

CENER：单位体积的总粘性耗散能

SENER：单位体积的总弹性应变能密度

SNETk：在第k个网络中的所有应力分量(0≤k≤10)。

如果平衡网络中指定了塑性或者使用了Mullinus,同样也可以输出他们对应的输出变量。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删