经典金属塑性模型(Classical metal plasticity):
使用伴随塑性流动的的Mises或Hill屈服面,分别允许各向同性和各向异性屈服;
采用理想塑性或各向同性硬化行为;
当速率依赖效应很重要时可以使用;
用于如碰撞分析,金属成形,和通用坍塌应用研究(在Abaqus中也支持包含运动硬化的塑性模型,因此更适合涉及循环加载的情况);
可用于任何具有位移自由度单元的求解;
可用于全耦合温度位移分析(Fully coupled thermal-stress analysis),全耦合热电结构分析(Fully coupled thermal-electrical-structural analysis),或绝热热应力分析(Adiabatic analysis),比如塑性耗散导致材料加热;
可以与Abaqus 中的渐进损伤和失效模型结合使用,从而指定不同的损伤起始标准和损伤演化规律,允许材料刚度的逐步退化和从网格中移除单元;
可以与Abaqus/Explicit中的剪切破坏模型结合使用,提供一个简单的延性动态破坏准则,允许从网格中移除单元,尽管通常推荐使用上述渐进损伤和失效方法;
可以与Abaqus/Explicit中的拉伸失效模型结合使用,以提供拉伸断裂标准,得到许多失效选择和从网格中移除单元;
必须与线性弹性材料模型或状态方程材料模型结合使用。
1. 屈服面
Mises和Hill屈服面假设金属的屈服与等效压应力无关:这一观察结果在正压应力下对大多数金属(除空心金属外)都得到了实验证实。但对于在高三轴拉伸条件下的金属可能是不准确的,因为在这种情况下,空腔可能在材料中成核和生长;这种情况可能出现在裂纹尖端附近的应力场和一些极端的热载荷情况下,例如可能发生在焊接过程中;针对这种情况,在Abaqus中提供了一个多孔金属塑性模型。
Mises屈服面:米塞斯屈服曲面用于定义各向同性屈服。它是通过给出单轴屈服应力值作为单轴等效塑性应变、温度和/或场变量的函数来定义的。在Abaqus/Standard中,屈服应力也可以在用户子程序UHARD中定义。

各向同性屈服
Hill屈服面:Hill屈服面允许对各向异性屈服进行建模。必须为金属塑性模型指定一个参考屈服应力σ0,并分别定义一组屈服比Rij。这些数据定义了每个应力分量对应的屈服应力为Rij σ0。屈服比可以用来定义与钣金成形相关的三种常见的各向异性:横向各向异性、平面各向异性和一般各向异性。

各向异性屈服
2. 硬化
在Abaqus中,可以定义理想塑性材料(没有硬化),或者可以指定加工硬化。各向同性硬化,包括Johnson-Cook硬化,可在Abaqus/Standard和Abaqus/Explicit中使用。此外,Abaqus还为经受循环加载的材料提供了随动硬化。

硬化
2.1 理想塑性
塑性是指屈服应力不随塑性应变而变化。它可以用表格形式定义一系列温度和/或场变量;每个温度和/或场变量的单一屈服应力值指定了屈服的开始。
2.2 各向同性硬化
各向同性硬化是指屈服面在所有方向上均匀地改变,使得塑性应变发生时屈服应力在所有应力方向上都增加(或减小)。Abaqus提供了一个各向同性硬化模型,这对于涉及总塑性应变的情况或在整个分析过程中每个点的应变基本上在应变空间中相同方向的情况是有用的。虽然该模型被称为“硬化”模型,但也可以定义应变软化或先硬化后软化。
如果定义了各向同性硬化,则屈服应力σ0可以作为塑性应变的表函数给出,如果需要,也可以作为温度和/或其他预定义的场变量的表函数给出。给定状态下的屈服应力是简单地从这个数据表中插值出来的,并且对于塑性应变超过表格数据给出的最后值,它保持常数。
Abaqus/Explicit将数据正则化到表中,这些表是根据自变量的偶间隔定义的。在某些情况下,如果屈服应力是在自变量(塑性应变)的不均匀间隔上定义的,并且自变量的范围比最小间隔大,那么Abaqus/Explicit可能无法在合理的间隔内获得数据的准确正则化。在这种情况下,程序将在处理完所有数据后停止,并提示必须重新定义材料数据的错误消息。
2.3 Johnson-Cook各向同性硬化
Johnson-Cook硬化是一种特殊类型的各向同性硬化,其中屈服应力是等效塑性应变、应变速率和温度的解析函数。这种硬化规律适用于包括大多数金属在内的许多材料的高速变形建模。Hill势函数不能用于Johnson-Cook硬化。
2.4 用户子程序
在Abaqus/Standard中,各向同性硬化的屈服应力σ0可以通过用户子程序UHARD来描述。
2.5 随动硬化
在Abaqus中提供了三种随动硬化模型来模拟金属的循环加载。线性随动模型近似于恒定硬化率的硬化行为。更一般的非线性各向同性/随动模型将给出更好的预测,但需要更详细的校准。多线性随动模型结合了多条分段线性硬化曲线来预测金属在热-力循环加载下的复杂响应。该模型基于Besseling(1958),仅在Abaqus/Standard中可用。
3. 流动法则
Abaqus使用关联塑性流。因此,当材料屈服时,非弹性变形率与屈服面法向一致(塑性变形体积不变)。对于大多数金属计算,这种假设通常是可以接受的;最明显的不合适的情况是,当金属板形成纹理并最终撕裂时,塑性流在金属板中的局部化的详细研究。只要这些影响的细节不是我们感兴趣的(或者可以从不太详细的标准中推断出来,比如达到由应变定义的成形极限),使用光滑的Mises或Hill屈服曲面的Abaqus中关联流动模型通常可以准确地预测这种行为。
4. 率相关性
随着应变率的增加,许多材料的屈服强度都有所增加。当应变速率在0.1 /s到1 /s之间时,这种效应在许多金属中变得重要;对于10 /s到100 /s的应变速率时是更加关键,这是高能动力事件或制造过程的特征。有多种方法可以引入应变率相关的屈服应力。
4.1 直接表格数据
试验数据以不同等效塑性应变率(ε˙¯ pl)下的屈服应力值与等效塑性应变的关系表的形式提供;一个应变速率使用一个表。直接表格数据不能与Johnson-Cook硬化一起使用。

率相关直接定义
4.2 屈服应力比
可以通过缩放函数指定应变速率依赖关系。在这种情况下,只输入一条硬化曲线,即静态硬化曲线,然后用静态关系表示速率相关的硬化曲线;也就是说,假设

式中σ0为静态屈服应力,ε¯pl为等效塑性应变,ε˙¯pl为等效塑性应变率,R为比值,定义为当ε˙¯pl= 0 时R = 1。

屈服应力比
4.3 用户子程序
在Abaqus/Standard用户子程序中,可以使用UHARD来定义速率相关的屈服应力。提供当前等效塑性应变和等效塑性应变率,并负责返回屈服应力和导数。
5. 渐进损伤与失效
在Abaqus中,金属塑性材料模型可以与渐进损伤和破坏模型结合使用。该功能允许指定一个或多个损伤起裂标准,包括ductile, shear, forming limit diagram (FLD), forming limit stress diagram (FLSD), Müschenborn-Sonne forming limit diagram (MSFLD), and, in Abaqus/Explicit, Marciniak-Kuczynski (M-K) criteria. 损伤发生后,材料刚度按照规定的损伤演化响应逐步退化。该模型提供了两种失效选择,包括由于结构 tearing or ripping而从网格中去除单元。渐进式损伤模型允许材料刚度的平滑退化,使其适用于准静态和动态情况,相比下述动态失效模型有很大的优势。

渐进损伤与失效模型

定义损伤演化
6. Abaqus/Explicit中的剪切和拉伸动态破坏
在Abaqus/Explicit中,金属塑性材料模型可以与剪切和拉伸破坏模型结合使用,适用于真正动态的情况;然而,上述渐进损伤和破坏模型通常是首选的。
6.1 剪切失效
剪切破坏模型提供了一种简单的破坏准则,适用于包括大多数金属在内的许多材料的高应变速率变形。它提供了两种失效选择,包括由于结构 tearing or ripping而从网格中去除单元。剪切破坏准则基于等效塑性应变的值,主要适用于高应变率、真正的动态问题。Abaqus/CAE中不支持剪切破坏模型操作定义。
6.2 拉伸失效
拉伸破坏模型使用静水压应力作为破坏度量来模拟动态剥落或压力切断。它提供了许多失效选择,包括单元移除。与剪切破坏模型类似,拉伸破坏模型适用于金属的高应变率变形,适用于真正的动态问题。Abaqus/CAE中不支持拉伸破坏模型操作定义。
7. 塑性做功产生的热量
Abaqus支持塑性耗散导致材料加热。热产生通常用于模拟大块金属成形或涉及大量非弹性应变的高速制造过程,其中由于材料性能的温度依赖性,由其变形引起的材料加热是一个重要的影响。它只适用于绝热热应力分析(adiabatic analysis)、全耦合温度位移分析(fully coupled thermal-stress analysis)或全耦合热电结构分析(fully coupled thermal-electric -structural analysis)。这种效应是通过定义非弹性耗散率的分数来引入的,该分数表现为每体积的热通量。

定义需要
Mechanical---Elasticity---Elastic
Mechanical---Plasticity---Plastic
Thermal---Specific Heat
General---Density
Thermal---Inelastic Heat Fraction
8. 初始条件
当我们需要研究已经经过某种加工硬化的材料的行为时,可以提供初始等效塑性应变值来指定与加工硬化状态相对应的屈服应力。需要在加载模块的预定义场定义:
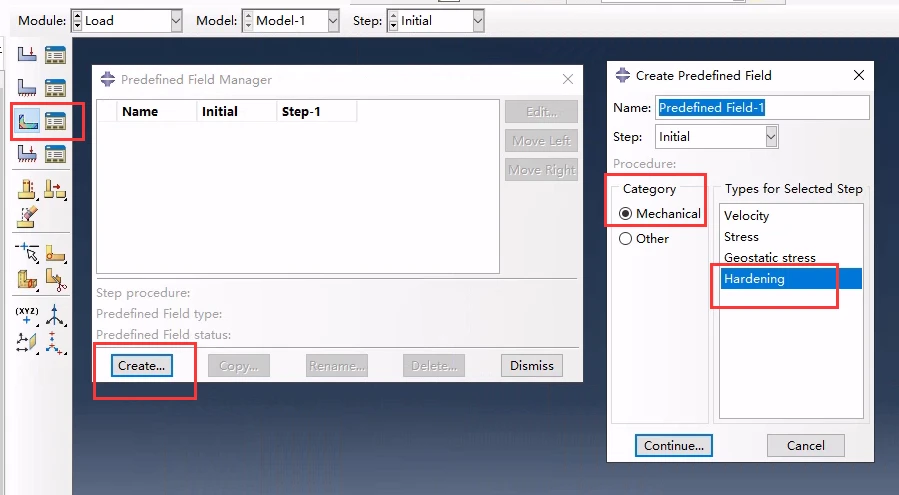
预定义硬化初始等效塑性应变

初始等效塑性应变
9. 单元与输出
经典的金属塑性可以用于任何包含力学行为的单元(具有位移自由度的单元)。
除了Abaqus中可用的标准输出标识符之外,以下变量对于经典金属塑性模型具有特殊意义:
PEEQ: 等效塑性应变;

等效塑性应变
其中:

初始等效塑性应变
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删