Abaqus材料属性定义：非弹性力学性能基础

1. 塑性理论

大多数工程材料最初都是弹性的。弹性行为意味着变形是完全可恢复的：当载荷被移除时，试件恢复到原来的形状。如果载荷超过某个极限(“屈服载荷”)，则变形不再是完全可恢复的。当载荷被移除时，某些部分的变形将会保留下来，例如，当回形针被弯得太大时，或者当金属坯在制造过程中被轧制或锻造时。塑性理论模拟了材料经历不可恢复变形的的力学响应。这些理论主要针对金属，但也适用于土壤、混凝土、岩石、冰、可破碎泡沫等。这些材料的表现方式各不相同。例如，大的纯静水压力值对金属的非弹性变形影响很小，但很小的静水压力值可能会对土样产生显著的、不可恢复的体积变化。尽管如此，塑性理论的基本概念是足够普遍的，已经成功地开发了适用于广泛材料的模型。

Abaqus中的塑性模型大多是“增量”理论，将机械应变率分解为弹性部分和塑性(非弹性)部分。增量塑性模型通常用：

① 屈服面：将“屈服载荷”认为是一个检验函数，可用于确定材料在特定的应力、温度等状态下是否为纯弹性响应；

② 流动规则：定义了物质点不再是纯弹性响应时发生的非弹性变形；

③ 定义硬化的演化规律：屈服 和/或 流动定义 随着非弹性变形的发生而变化的方式。

Abaqus/Standard还有一个“变形”塑性模型，其中应力由总机械应变定义。即Ramberg-Osgood模型，它主要用于韧性断裂力学应用，通常需要全塑性求解。

2. 弹塑性分析中的弹性响应

Abaqus塑性模型还需要一个弹性定义来处理应变的可恢复部分。

在进行有限应变弹塑性分析时，Abaqus假设塑性应变主导变形，弹性应变很小。这个限制是由Abaqus使用的弹性模型施加的。这是合理的，因为大多数材料都有一个明确的屈服点，一般均比杨氏模量小很多，例如，金属的屈服应力通常小于材料杨氏模量的1%；因此，弹性应变也将小于该百分比，并且材料的弹性响应可以非常精确地建模为线弹性。

在Abaqus/Explicit中，弹性应变能是以增量的形式更新的。弹性应变能增量(ΔEs)由ΔEs = ΔEt−ΔEp计算，其中ΔEt为总应变能增量，ΔEp为塑性耗能增量。对于几乎全部为塑性变形的增量，ΔEs比ΔEt和ΔEp小得多。Δ E t和Δ E p的近似计算会导致与真实解的偏差，虽然与Δ E t和Δ E p相比不显著，但对于Δ E s可能是显著的。通常情况下，弹性应变能解是相当准确的，但在一些罕见的情况下，Δ E t和Δ E p计算中的近似值可能导致弹性应变能结果为负值。这些负值最可能出现在率相关的塑性分析中。只要弹性应变能的绝对值与总应变能相比很小，弹性应变能的负值不应被认为是一个严重的求解问题。

3. 应力和应变的测量与输入

大多数材料表现出延性行为(大的非弹性应变)，屈服的应力水平数量级地小于材料的弹性模量，这意味着相关的应力和应变测量是“真”应力(柯西应力)和对数应变。因此，材料数据应该以真实应力和对数应变的形式给出。

材料是各向同性时，单轴测试的名义应力-应变数据可以简单地转换为真实应力和对数塑性应变：式中E为弹性模量；

   真实应力和对数应变的转换公式
 

3.1 应力应变输入数据的举例：

以具有各向同性硬化的经典金属塑性模型的材料数据输入为例，表征材料硬化行为的应力-应变数据是定义模型所必需的。实验硬化曲线可能如图1所示。

   图1
 

200Mpa (29000 lb/in2)时发生屈服。然后材料在1%的应变时硬化到300 MPa (43511 lb/in2)，之后它是完全塑性的。假设杨氏模量为200000 MPa (29 × 106 lb/in2)，则1%应变点的塑性应变为0.01−300/200000= 0.0085。当单位是牛顿和毫米时，压力的单位对应于MPa（Abaqus单位制统一查询表），因此，输入数据为：

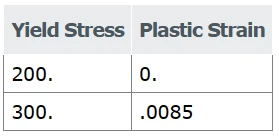
   塑性数据的输入
 

采用塑性应变值而不是总应变值定义硬化行为。此外，第一个数据对必须与塑性的开始相对应(第一行的塑性应变值必须为零)。这些概念适用于以表格形式定义硬化数据的任何塑性模型。

3.2 指定初始等效塑性应变：

在Abaqus中，对于使用经典金属塑性(classical metal plasticity)或Drucker-Prager塑性(Extended Drucker-Prager models)的单元，可以通过定义初始硬化条件指定等效塑性应变的初始值。等效塑性应变(输出变量PEEQ)包含等效塑性应变的初始值加上分析过程中由于塑性变形而产生的附加等效塑性应变。然而，塑性应变张量(输出变量PE)仅包含分析过程中塑性变形产生的应变量。图2中的简单一维示例说明了这个概念。

   图2
 

材料在A点处于退火态，其屈服应力为σ0B。然后沿着路径(A, B, C, D)加载硬化；对于此时，材料的新屈服应力变为σ0E。且新的分析采用与第一次分析相同的硬化曲线，即沿着路径(D, E, F)；从点D开始，总应变为ε2，其中塑性应变εpl 2可以通过输出变量PE11输出。为获得材料真实的屈服应力σ0E，应提供E点的等效塑性应变 εpl 1作为初始条件。类似地，F点的屈服应力由等效塑性应变PEEQ = εpl 1 + εpl 2得到。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删