非弹性力学性能：Abaqus材料属性定义之率相关屈服

率相关屈服：

当屈服强度依赖于应变速率且预期应变速率显著，并需要精确定义材料的屈服行为时使用；

仅适用于各向同性硬化金属塑性模型(Mises, Johnson-Cook, and Hill)，非线性各向同性/随动塑性模型的各向同性分量，扩展的Drucker-Prager塑性模型和可破碎泡沫塑性模型；

通过提供各向同性硬化金属塑性模型、非线性各向同性/随动塑性模型的各向同性分量以及扩展的Drucker-Prager塑性模型的表格数据，可以方便地根据加工硬化参数和场变量进行定义;

可通过定义用户自定义的超应力幂律参数、屈服应力比或Johnson-Cook率依赖参数来定义(最后一个选项不适用于可破碎泡沫塑性模型，是Johnson-Cook塑性模型唯一可用的选项)；

不能与任何Abaqus/Standard蠕变模型一起使用(金属蠕变，随时间的体积膨胀，Drucker-Prager蠕变或cap蠕变)，因为蠕变行为已经是一个速率相关的机制；

在动态分析中，应规定屈服应力随应变率的增加而增加。

1. 加工硬化依赖

一般来说，材料的屈服应力¯σ(对于可破碎泡沫模型是¯B)依赖于加工硬化，对于各向同性硬化模型，通常用等效塑性应变¯ε pl ，非弹性应变率˙¯ε pl，温度 θ，以及预定义的场变量 fI 来表示：

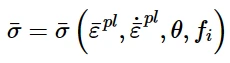
   屈服应力的表示
 

许多材料的屈服强度随着应变率的增加而增加；当应变率在0.1~1 s-1之间时，这种效应在许多金属和聚合物中变得重要，并且对于应变率10~100 s-1变得非常重要，这是高能量动态事件或制造过程的特征。

2. 定义各种材料模型的硬化依赖关系

应变率依赖性可以通过直接输入不同应变率下的硬化曲线来定义，也可以通过定义屈服应力比来单独指定率依赖性。

2.1 直接输入测试数据

加工硬化依赖关系通常可以作为各向同性硬化Mises塑性模型、非线性各向同性/随动硬化模型的各向同性分量以及扩展的Drucker-Prager塑性模型的表格数据来给出。测试数据以不同等效塑性应变率下屈服应力值与等效塑性应变的表格形式输入。屈服应力必须作为等效塑性应变的函数给出，如果需要，还可以作为温度和其他预定义的场变量的函数给出。在有限应变下定义这种相关性时，应使用“真”(柯西)应力和对数应变值。每个温度下的硬化曲线必须总是从零塑性应变开始。对于理想塑性，在每个温度下只能定义一个屈服应力，且塑性应变为零。可以将材料定义为应变软化和应变硬化。根据需要重复加工硬化数据，以定义不同应变速率下的应力-应变曲线。所求应变和应变率下的屈服应力直接从这些表中插值出来。在Abaqus/CAE中不支持循环硬化。

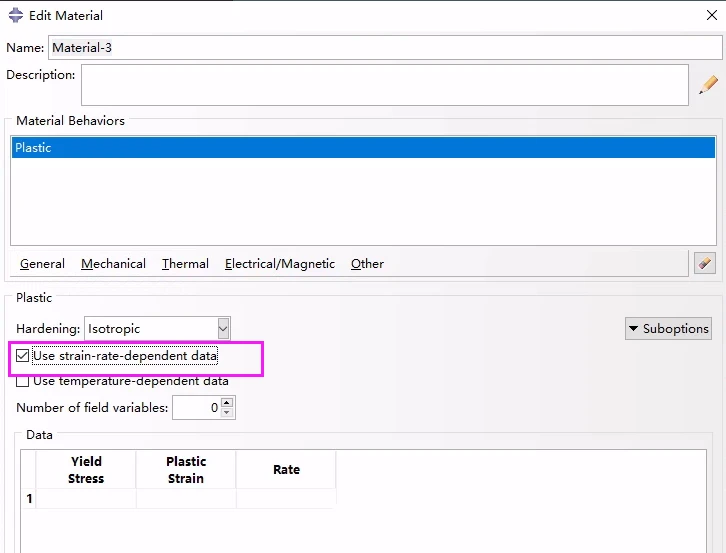
   对于金属
 

对于岩石材料，应该采用Drucker–Prager准则，通过以下方法定义：

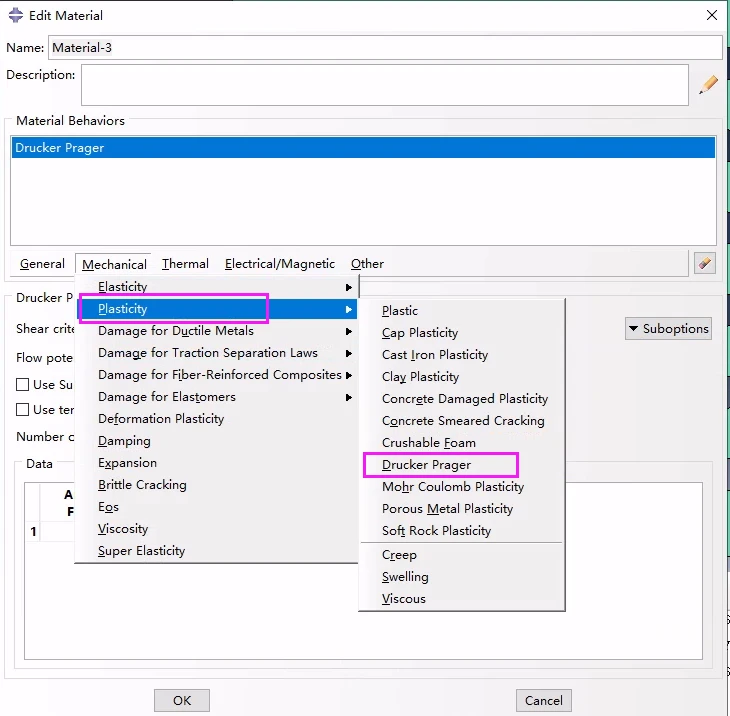
   对于岩石
 

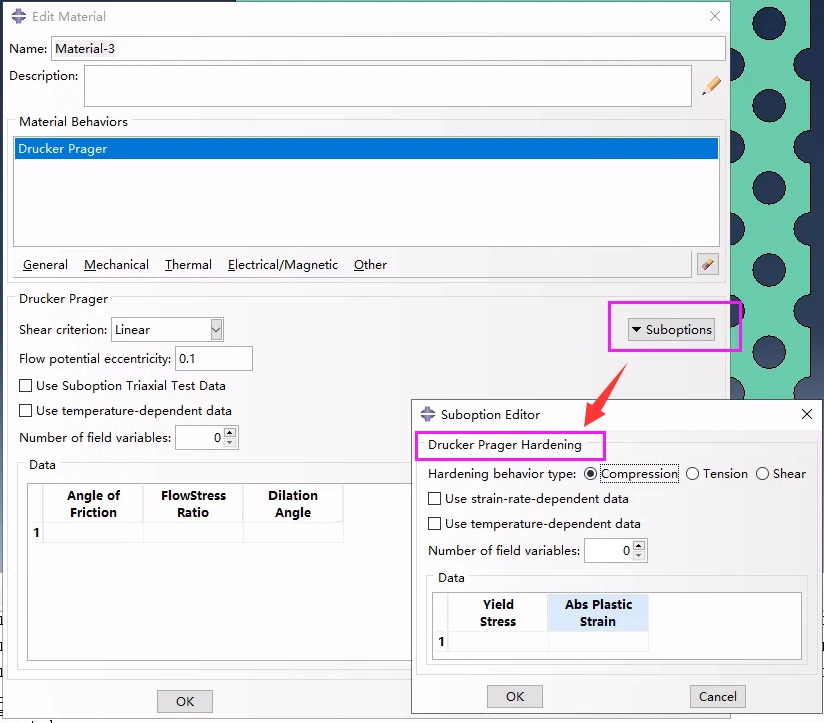
   对于岩石定义率相关性
 

2.2 使用屈服应力比

另外，作为定义Johnson-Cook模型和可破碎泡沫塑性模型的率相关屈服应力的唯一方法，应变率行为可以被假设为可分离的，因此应力-应变依赖关系在所有应变率水平上是相似的：

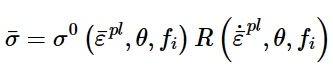
   屈服应力
 

其中σ 0(¯ε pl， θ， f i)(或泡沫模型中的B(¯ε pl， θ， f i)为静态应力-应变行为，R(˙¯ε pl， θ， f i)为非零应变率下屈服应力与静态屈服应力之比 (且 R (0， θ， f i) = 1.0)。

在Abaqus中定义R提供了三种方法：指定一个超应力幂律，将R直接定义为表格函数，或指定解析Johnson-Cook形式来定义R。

超应力幂律  Overstress power law：

Cooper - Symonds超应力幂律有这样的形式：

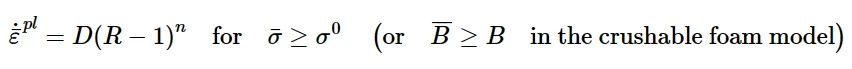
其中D (θ， fi)和n (θ， fi)是材料参数，在CAE中定义给出表数据，可以是温度的函数，也可以是其他预定义场变量的函数。

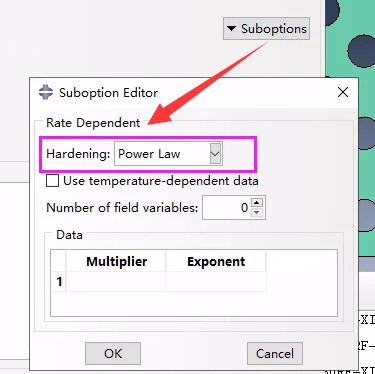
   Mulitiplier 大小： Material parameter, D. 材料参数
   

   Exponent 指数：Material parameter, n. 材料参数 
   

表函数 Tabular function:

R也可以直接作为等效塑性应变率˙¯ε p1(或可破碎泡沫模型单轴压缩试验中的轴向塑性应变率)、温度 θ和场变量 f I的表函数。

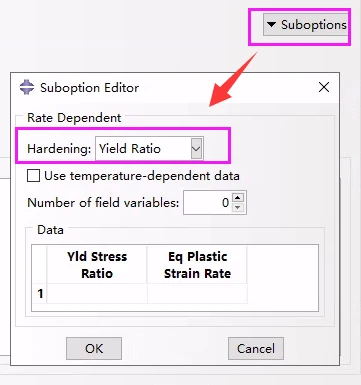
   Yld Stress Ratio ：屈服应力比, R=σ¯/σ0
   

   Eq Plastic Strain Rate ： 等效塑性应变率 (或 可破碎泡沫模型对应单轴压缩时的轴向塑性应变率绝对值） 
   

Johnson-Cook率相关性 Johnson-Cook rate dependence：

Johnson-Cook率依赖遵循以下计算：

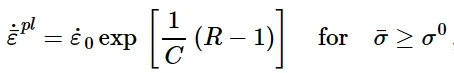
其中˙ε 0和C是不依赖于温度的材料常数，假设它们不依赖于预定义的场变量。Johnson-Cook率依赖关系可与Johnson-Cook塑性模型、各向同性硬化金属塑性模型、扩展Drucker-Prager塑性模型结合使用。(不能与可破碎泡沫塑性模型结合使用)。且是Johnson-Cook塑性模型中唯一可用的速率依赖形式。

   C ： 材料常数C，它与温度和场变量无关。
   

   Epsilon dot zero ： 材料常数 ˙ε 0, 与温度和场变量无关。
 

3. 单元

率相关屈服可用于包含力学行为的所有单元(即具有位移自由度的单元)。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删