Abaqus/Standard中经典的偏金属蠕变行为:
可以使用用户子程序CREEP或通过提供参数作为一些简单蠕变规律的输入来定义;
可以模拟各向同性蠕变(使用Mises应力势)或各向异性蠕变(使用Hill各向异性应力势);
仅在使用温度-位移耦合求解、瞬态土壤固结过程和准静态求解的分析步中可用;
要求将材料的弹性定义为线弹性行为;
可进行修改,以执行核标准NEF 9-5T《1类高温核系统部件设计指南和程序》中规定的辅助蠕变硬化规则,这些规则通过橡树岭国家实验室开发的本构模型来执行(ORNL模型);
可与蠕变应变率控制结合使用,其中蠕变应变率必须控制在一定范围内;
如果各向异性蠕变和塑性同时发生,可能会导致计算蠕变应变的误差。
Abaqus/Standard中的率相关的垫片行为:
使用单向蠕变作为垫片厚度方向行为模型的一部分;
可以使用用户子程序CREEP或通过提供参数作为一些简单蠕变规律的输入来定义;
仅可在使用准静态求解的分析步中使用;
要求使用弹塑性模型来定义垫片厚度方向行为的速率无关部分;
Abaqus/Standard中的体积溶胀特性:
可以使用用户子程序CREEP或通过提供表格输入来定义;
可以是各向同性或各向异性;
仅在使用温度-位移耦合求解、瞬态土壤固结过程和准静态求解的分析步中可用;
要求将材料的弹性定义为线弹性行为。
1. 蠕变行为:
首先解释一下什么是蠕变哈:蠕变可以理解为施加持续相同的力(或应力),变形(或应变)随时间的变化。与应力松弛的概念对应,即施加持续相同的变形(或应变),力(或应力)随时间的变化。总之,蠕变和应力松弛均是与时间相关的性能。与弹性相关的时间效应为粘弹性,那么与塑性相关的时间效应为粘塑性。
蠕变行为由等效单轴行为-蠕变“定律”来指定。在实际情况下,蠕变规律通常是非常复杂的形式,以拟合实验数据;因此,这些规律是用用户子程序CREEP来定义的,如下所述。另外,在Abaqus/Standard中提供了五种常见的蠕变定律:幂律the power law、双曲正弦律 the hyperbolic-sine law、双幂律 the double power law、Anand律和Darveaux律。这些标准蠕变定律用于模拟二次或稳态蠕变。蠕变是通过在材料模型定义中包含蠕变行为来定义的。或者,可以将蠕变与垫片性能一起定义,以定义垫片的速率相关性能。
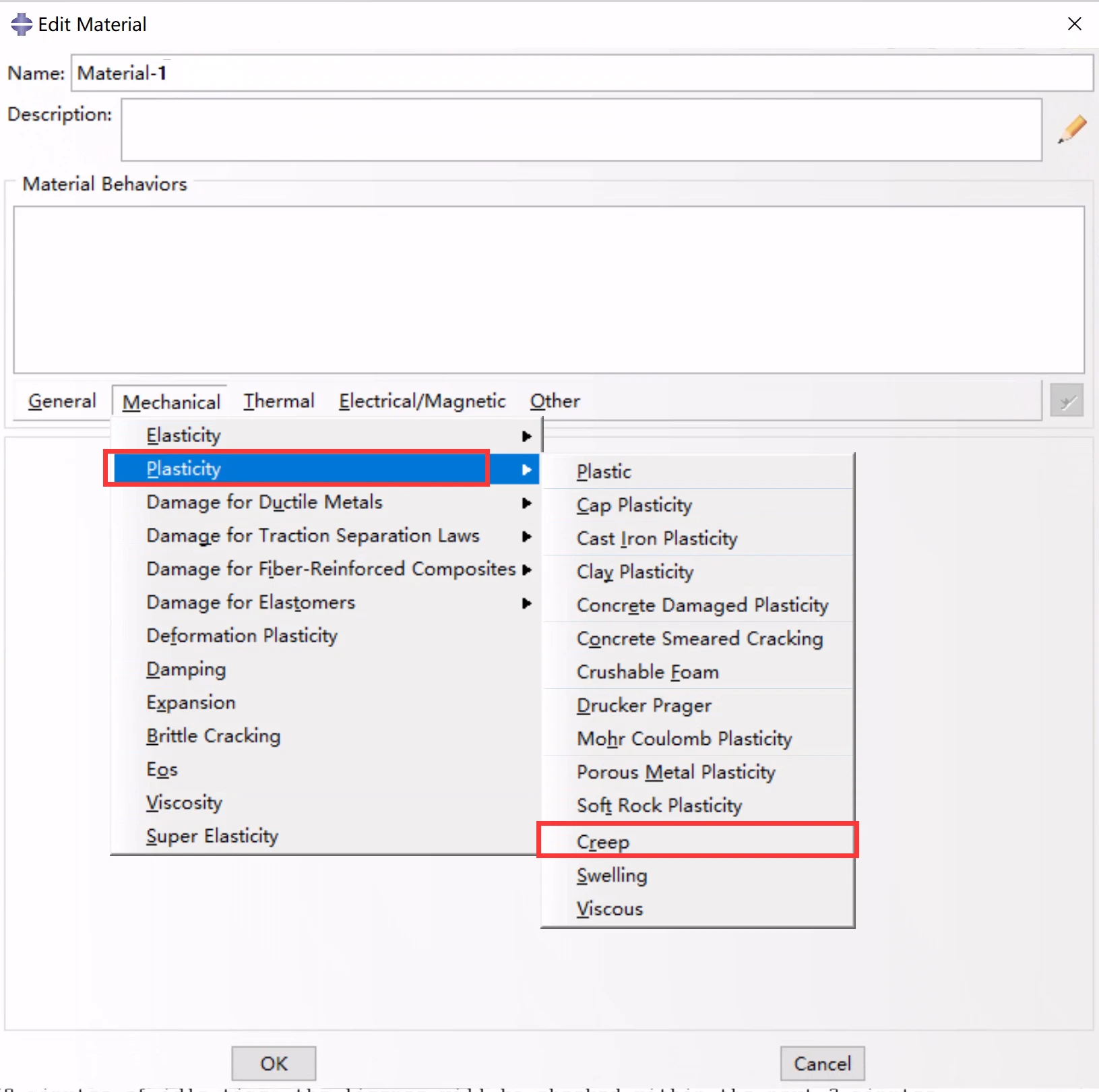
CAE中的定义
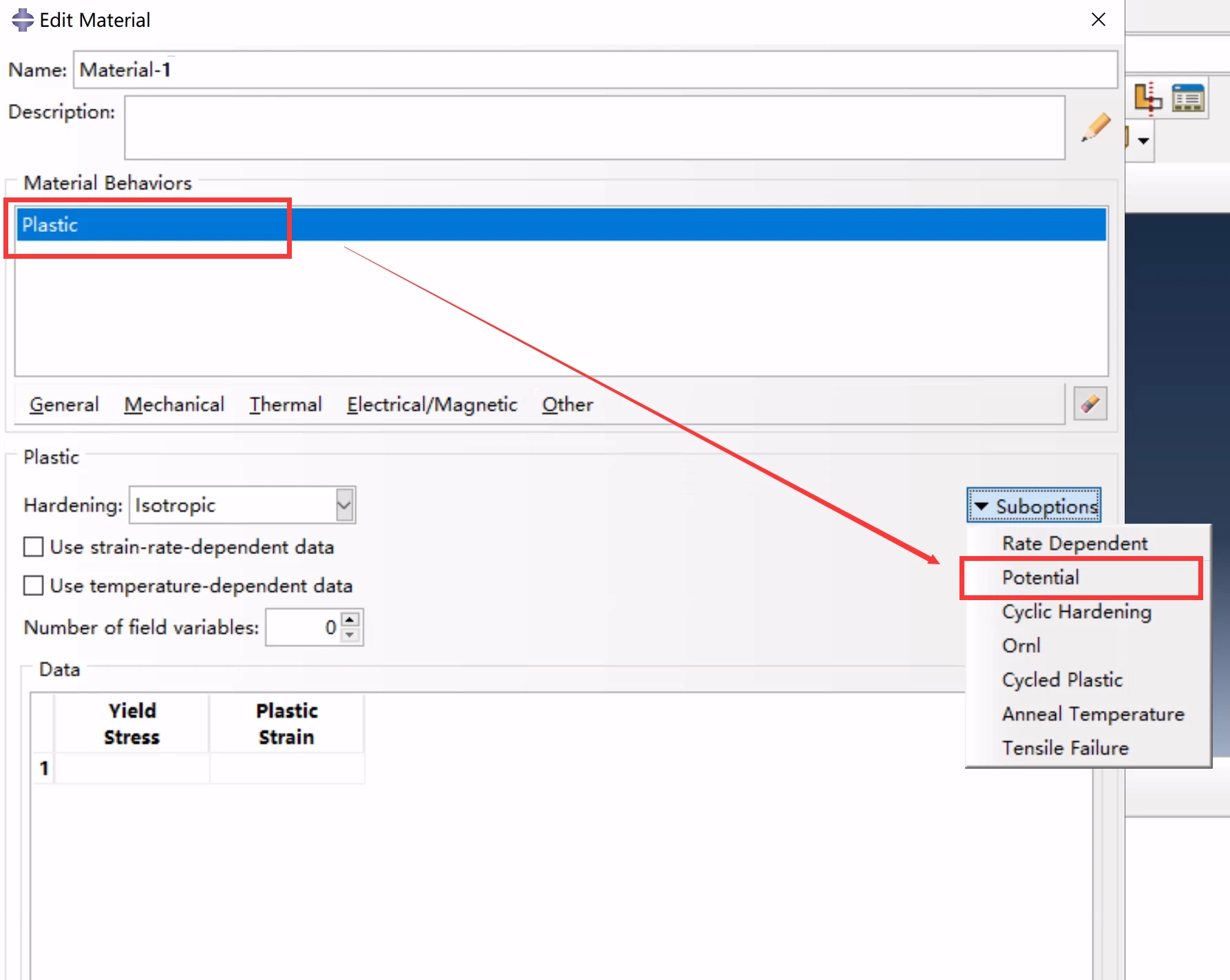
1.1 选择一种蠕变模型
幂律蠕变模型具有简单性,然而应用范围有限。幂律蠕变模型的时间硬化形式通常只在应力状态基本保持恒定的情况下才被推荐。当应力状态在分析过程中发生变化时,应使用幂律蠕变的应变硬化形式。在应力恒定且不存在温度和/或场依赖性的情况下,幂律蠕变定律的时间硬化和应变硬化形式是等效的。对于幂律的任何一个形式,应力都应该相对较低。
在高应力区域,如裂纹尖端附近,蠕变应变率经常表现为应力的指数依赖关系。双曲正弦蠕变规律在高应力水平下与应力σ呈指数相关(σ / σ 0远大于1,其中σ 0为屈服应力),在低应力水平下降低为幂律蠕变规律(无明显的时间依赖关系)。
双幂律,Anand和Darveaux模型特别适合于模拟电子封装中使用的焊料合金的行为,并已被证明可以在广泛的温度和应变率范围内产生准确的结果。
以上模型均不适合模拟循环荷载作用下的蠕变。ORNL模型(ORNL -橡树岭国家实验室本构模型)是不锈钢的经验模型,它可以给出循环加载的近似结果,而无需进行数值模拟。通常,循环加载的蠕变模型是复杂的,必须添加到具有用户子程序CREEP或用户子程序UMAT的模型中。
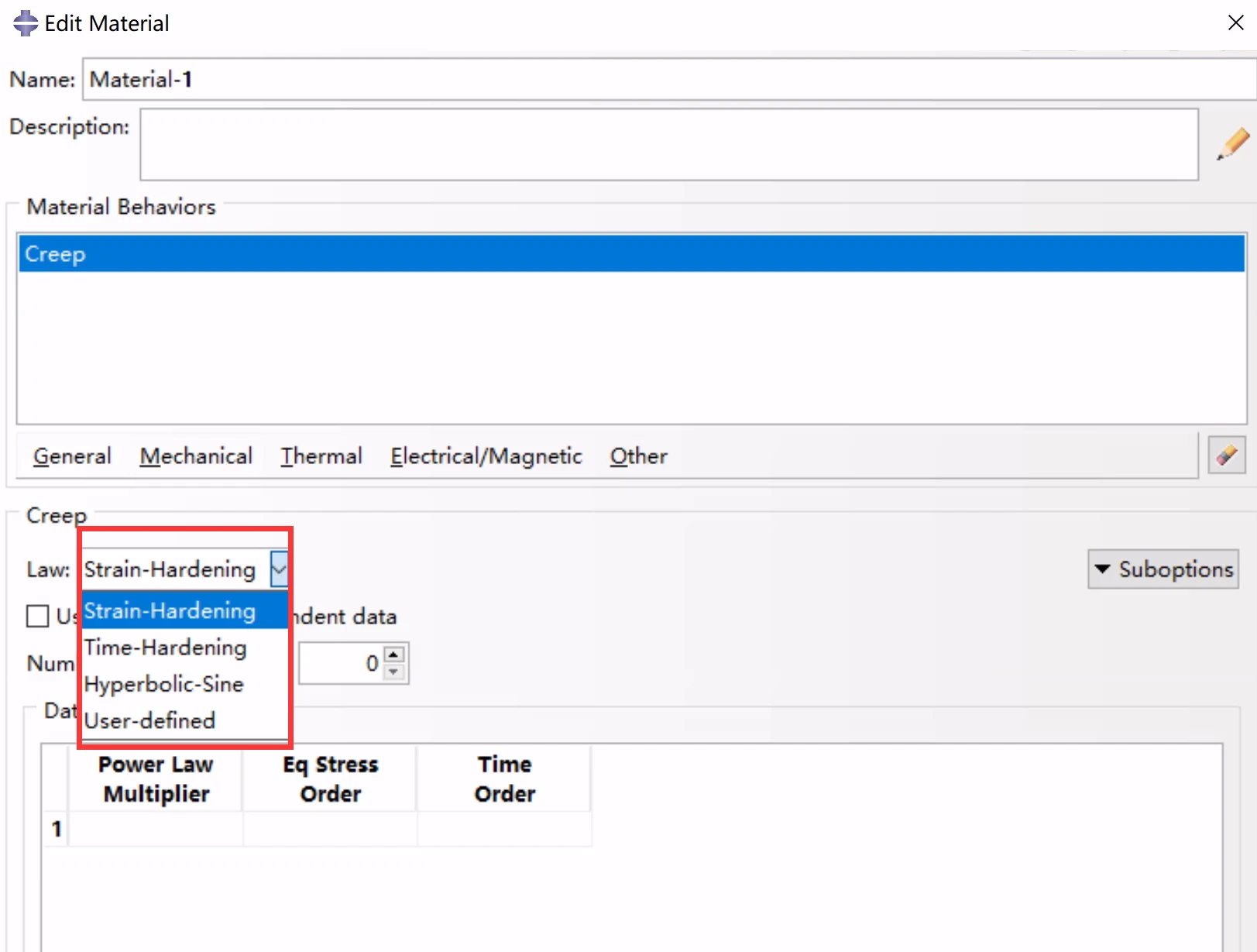
选择一种蠕变律
1.2 同时建立蠕变和塑性
如果蠕变和塑性同时发生,且隐式蠕变积分有效,则两种行为可能相互作用,需要求解一个耦合的本构方程系统。如果蠕变和塑性是各向同性的,即使弹性是各向异性的,Abaqus / Standard 也适当地考虑了这种耦合行为。但是,如果蠕变和塑性是各向异性的,那么Abaqus/Standard在对蠕变方程进行积分时不考虑塑性,这可能导致蠕变应变出现较大误差。这种情况只有在塑性和蠕变同时使用的情况下才会发生,比如在长期荷载增加期间会发生的情况;如果存在塑性占主导地位的短期预压阶段,然后是没有进一步屈服的蠕变阶段,则不会出现问题。
☆ 幂律模型 Power-law model:
幂律模型可以采用“时间硬化”形式,也可以采用相应的“应变硬化”形式。
& 时间硬化形式Time hardening form:
“时间硬化”形式是幂律模型两种形式中较简单的一种:
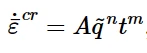
时间硬化的幂律模型
其中:
˙¯εcr 是单轴等效蠕变应变率;
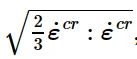
单轴等效蠕变应变率
˜q 是单轴等效偏应力;t 为总时间或蠕变时间,A, n, and m可以定义为温度的函数。
˜q是Mises等效应力或Hill各向异性等效偏应力,取决于定义的是各向同性蠕变行为还是各向异性蠕变行为。对于物理上合理的行为,A和n必须是正的,−1 <m ≤ 0。
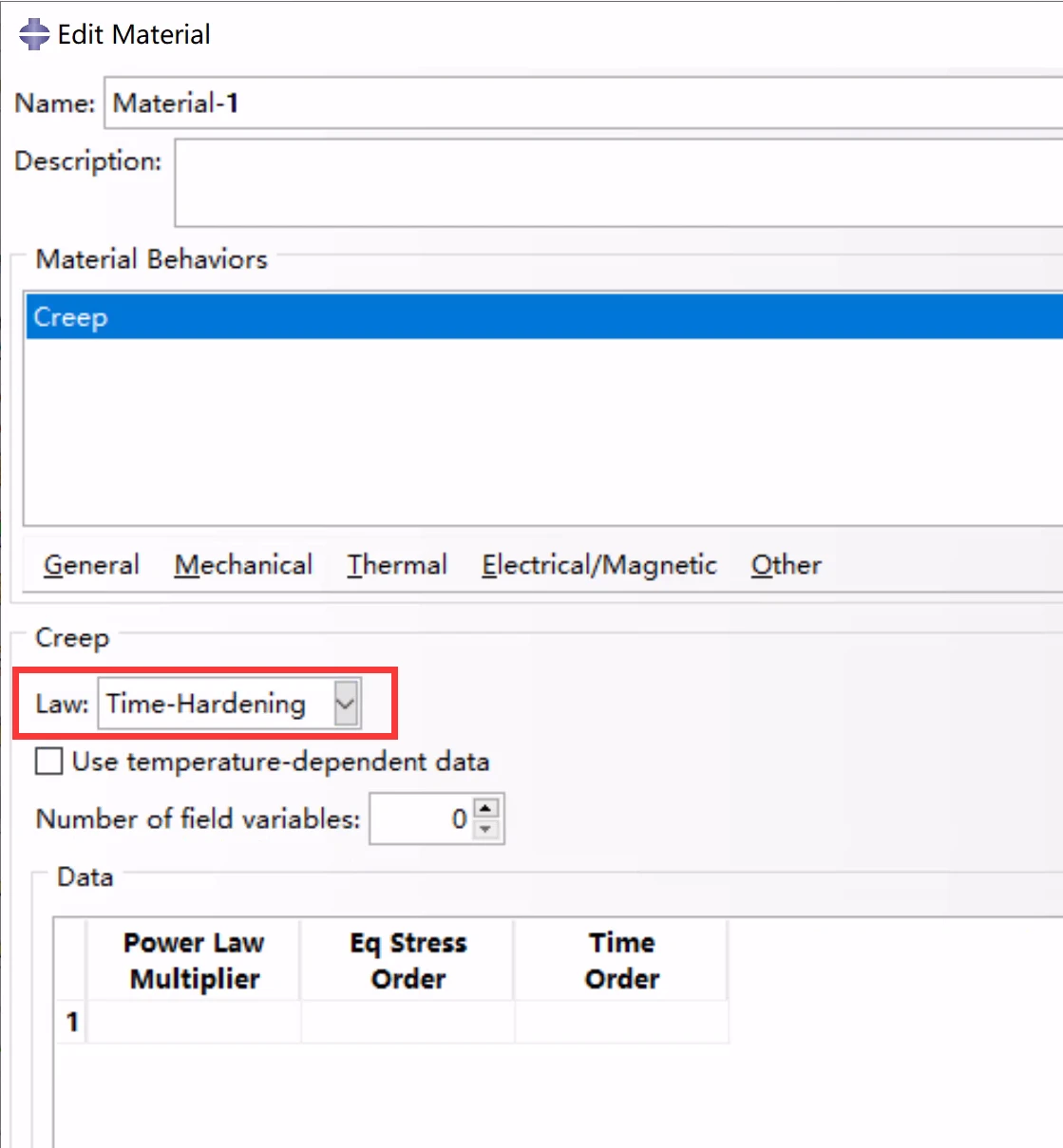
时间硬化形式
Power Law Multiplier:幂律乘数,A。
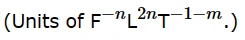
A的单位量纲
Eq Stress Order:等效偏应力阶,n。
Time Order:时间硬化蠕变规律的总时间阶数 m,应变硬化蠕变规律的总应变阶数 m。
& 时间依赖的行为Time-dependent behavior:
在时间硬化幂律模型中,可以使用总时间或蠕变时间。总时间是所有一般分析步的累积时间。蠕变时间是具有随时间变化的材料性能的过程时间的总和。如果使用总时间,建议对于分析中蠕变不活跃的任何分析步,使用与蠕变时间相比的小步长;这对于避免后续步骤中硬化行为的变化是必要的。在Abaqus/CAE中不支持指定时间类型。
& 应变硬化形式:
幂律的“应变硬化”形式为:
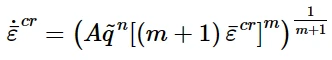
幂律的应变硬化
其中˙¯ε cr 和 ˜q定义同上,¯ε cr为等效蠕变应变。
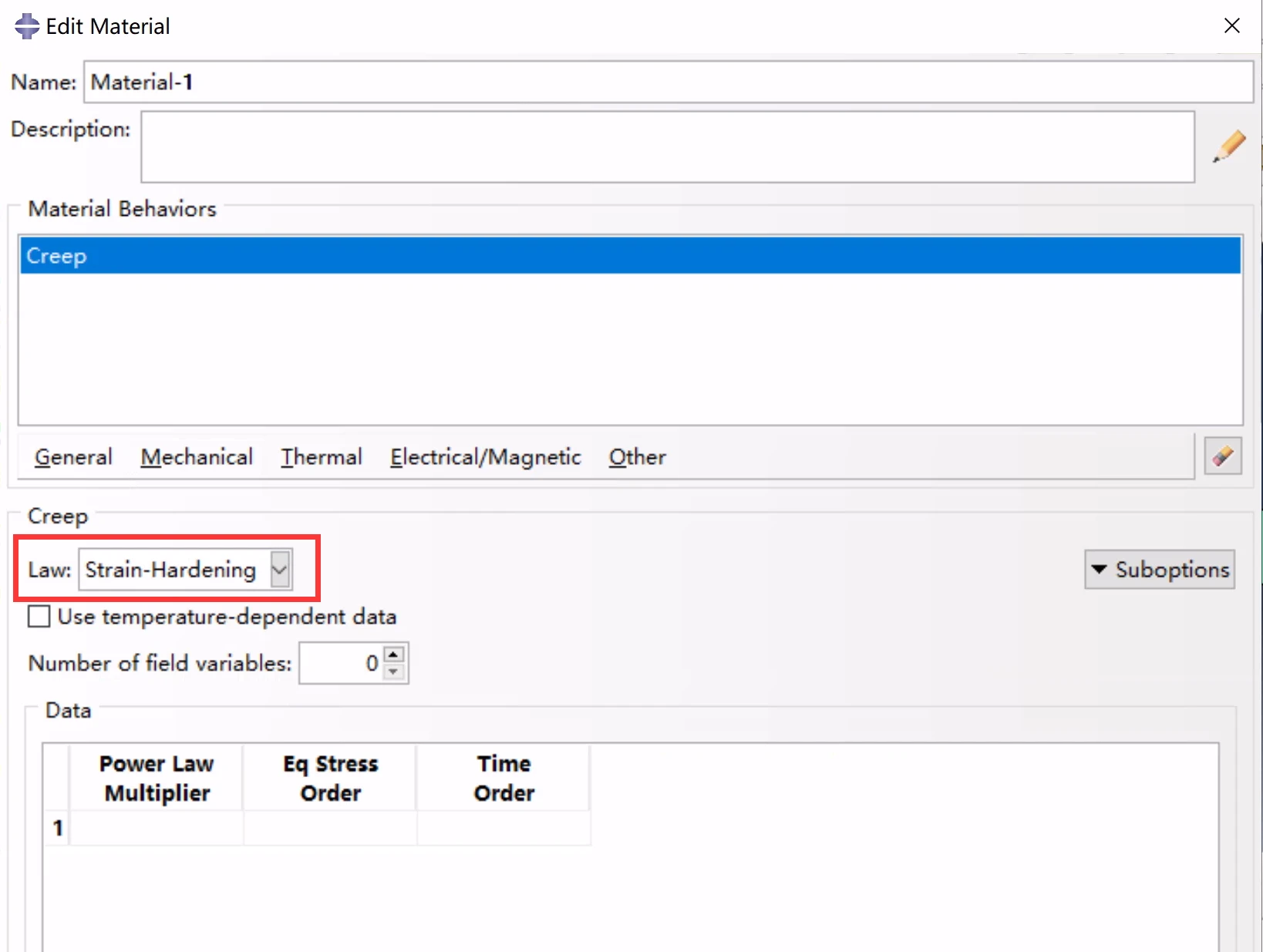
应变硬化定义
& 数值困难Numerical difficulties:
根据幂律形式的单位选择,对于典型的蠕变应变率,A的值可能非常小。如果A小于10的−27次方,则数值困难会导致计算错误;因此,采用另一种单位制可以避免蠕变应变增量计算的困难。
☆ 双曲正弦律模型 Hyperbolic-sine law model:
双曲正弦定律有如下形式:

双曲正弦模型
其中,˙¯ε c r和~q如上所述定义,θ为温度,θZ 为所使用温标上用户自定义的绝对零度值,
△H是活化能,R是通用气体常数,A、B、n为其他材料参数。
该模型包含了温度依赖性,这在上式中是很明显的;然而,参数A、B、n、△H、R不能定义为温度的函数。
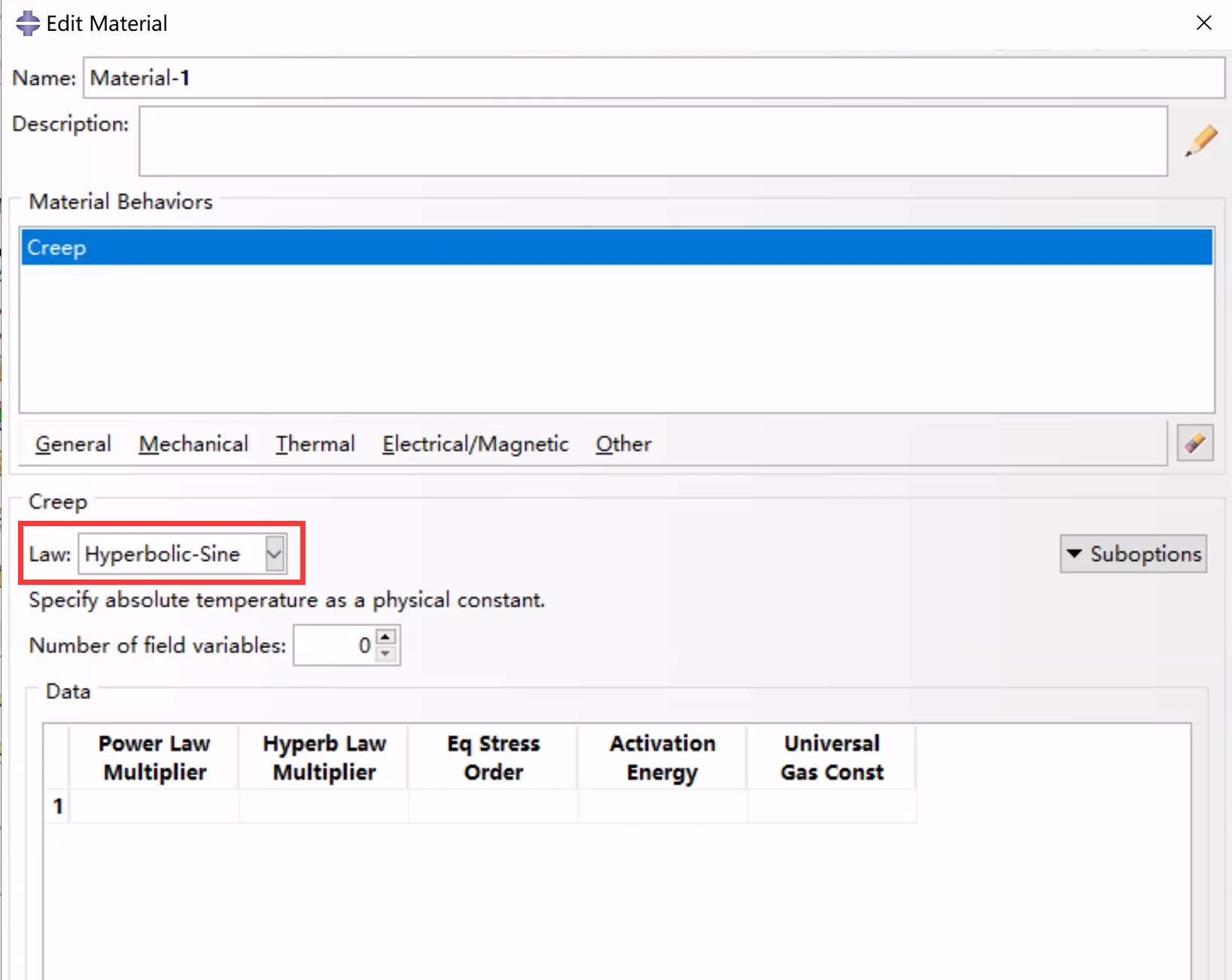
双曲正弦模型
Power Law Multiplier:幂律乘数 A,

A 的量纲
Hyperb Law Multiplier: 双曲正弦乘数,B,

B的量纲
Eq Stress Order:等效应力阶,n
Activation Energy: 活化能, △ H

△ H量纲
Univeral Gas Const:通用气体常数,R
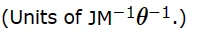
R的量纲
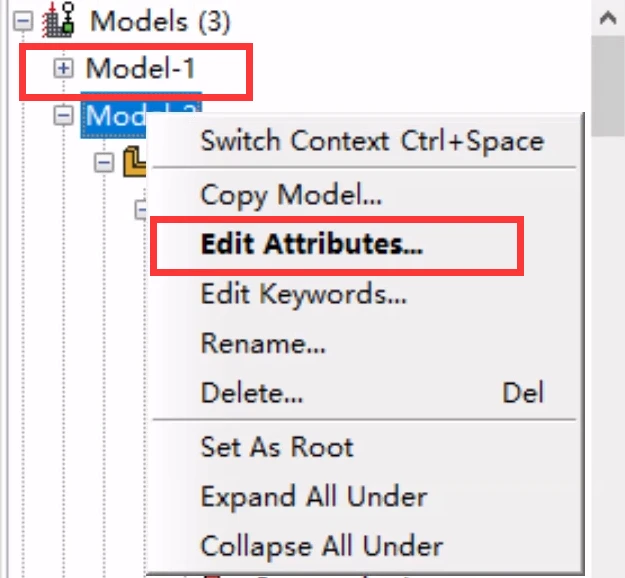
模型树右键编辑属性
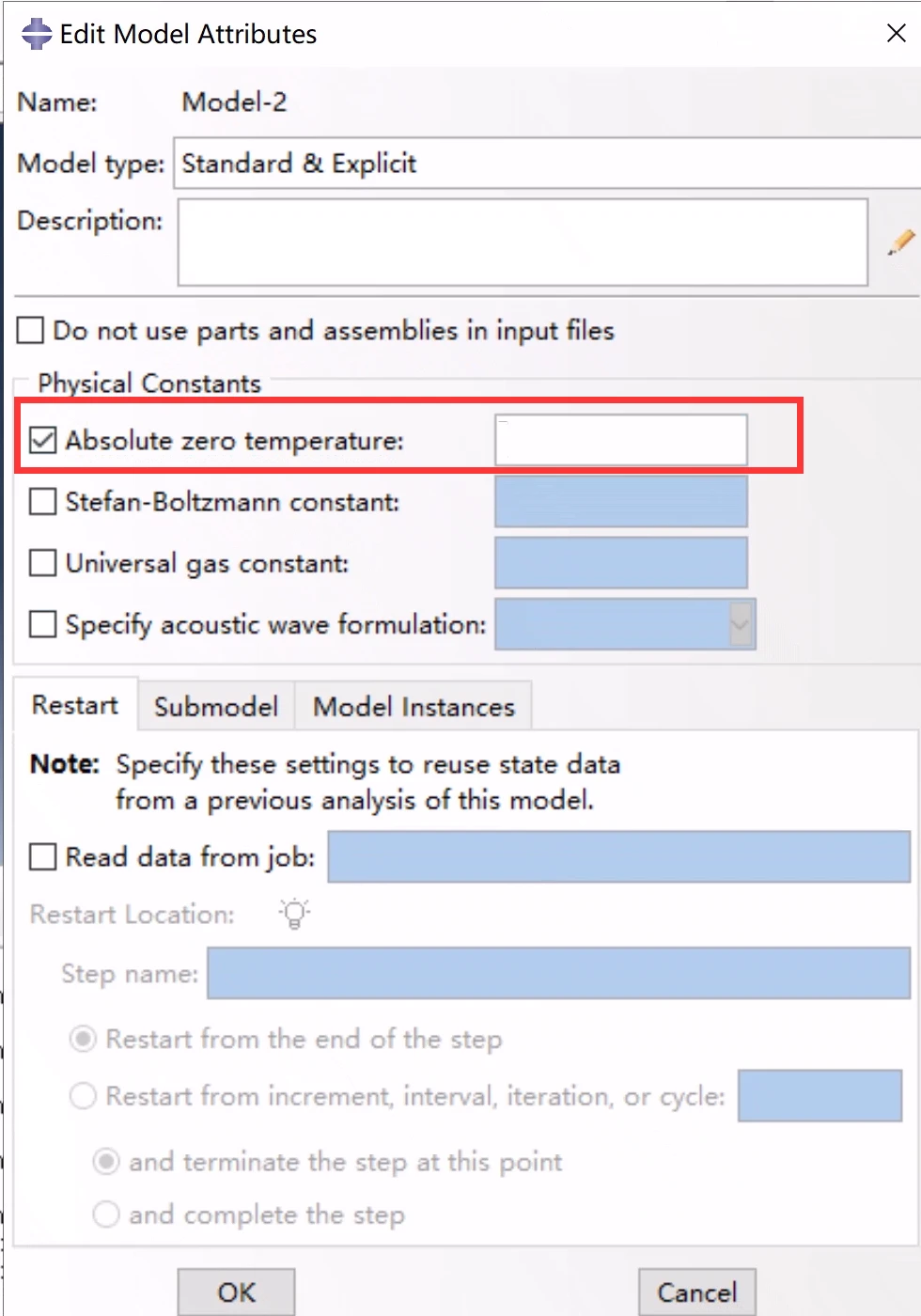
定义绝对零度
☆Anand model,Double power model 和 Darveaux model不支持在Abaqus/CAE定义;
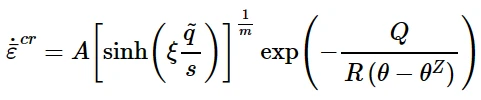
Anand model
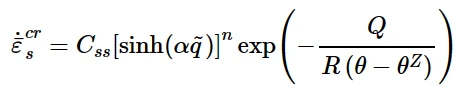
Double power model
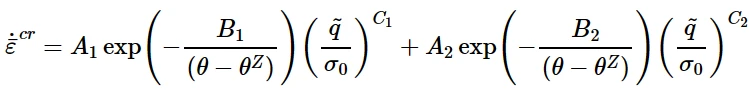
Darveaux model
☆ 各向异性蠕变 Anisotropic creep:
可以定义各向异性蠕变来指定Hill函数中的应力比。当计算蠕变应变率时,必须在每个方向上定义用于缩放应力值的比率Ri j。比率可以定义为常数或依赖于温度和其他预定义的场变量。比率是根据用户定义的局部材料方向或默认方向来定义的。当蠕变用于定义与速率相关的垫片行为时,各向异性蠕变不可用,因为只有垫片厚度方向行为才能具有与速率相关的行为。
各向异性蠕变定义
2. 体积溶胀行为
与蠕变定律一样,体积膨胀定律通常是复杂的,并且在用户子程序CREEP中最方便指定。但是,也提供了一种表格输入方式:
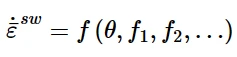
体积溶胀
其中˙¯ε sw是由膨胀引起的体积应变率,f1、f2、…是预定义的场,例如涉及核辐射效应的辐照通量。最多可以指定6个预定义场。
体积膨胀不能用于定义与速率相关的垫片行为。
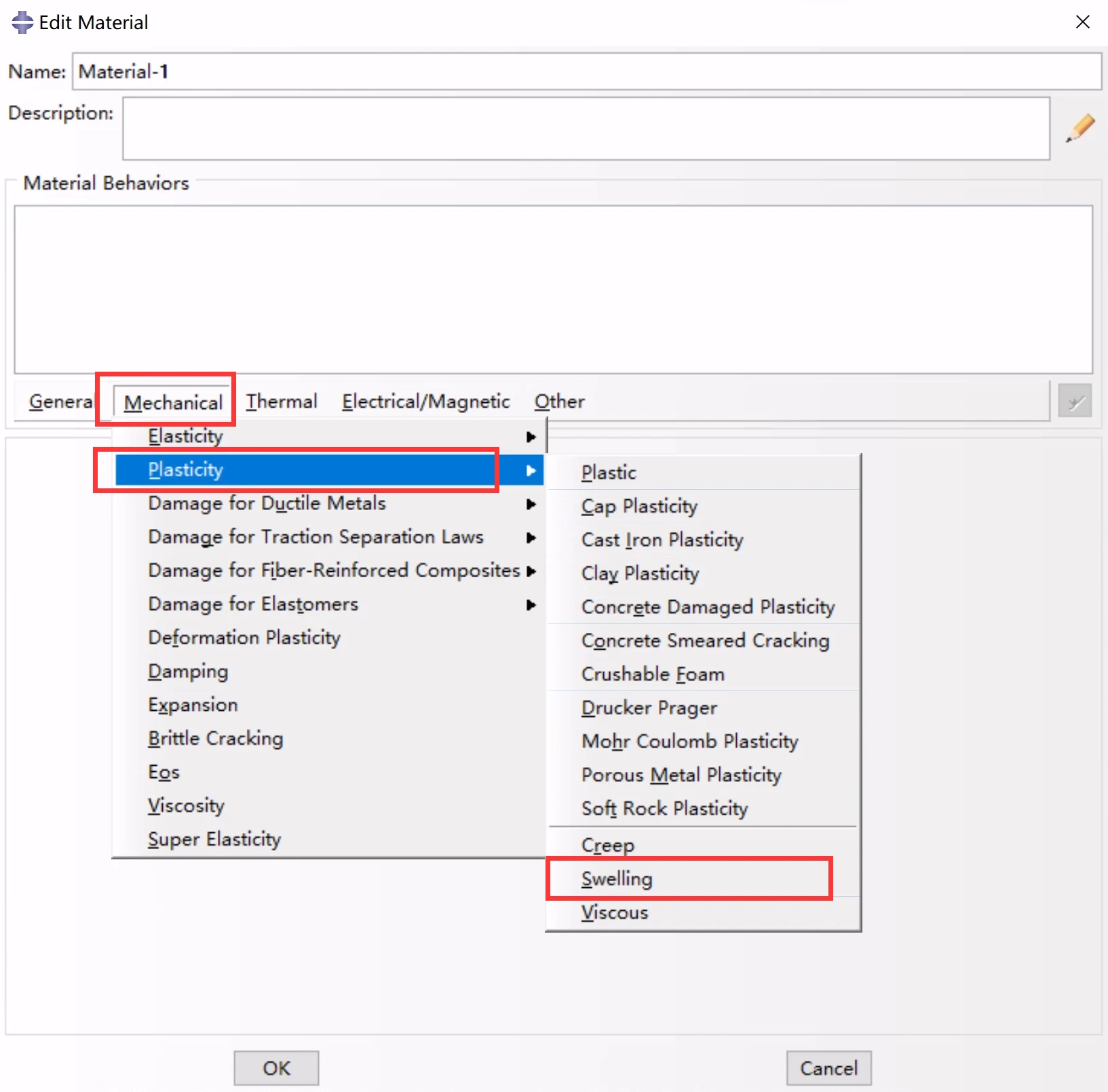
溶胀的定义
2.1 各向异性溶胀
各向异性可以很容易地包括在溶胀行为中。如果定义各向异性溶胀行为,则各向异性溶胀应变率表示为:
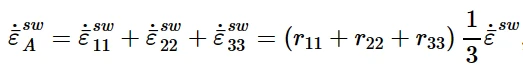
其中˙¯ε sw是体积溶胀应变率,可以直接或在用户子程序CREEP中定义。比率r 11、r 22和r 33也是用户自定义的。溶胀应变率分量的方向由局部材料方向定义,可以是用户定义的方向,也可以是默认的方向。
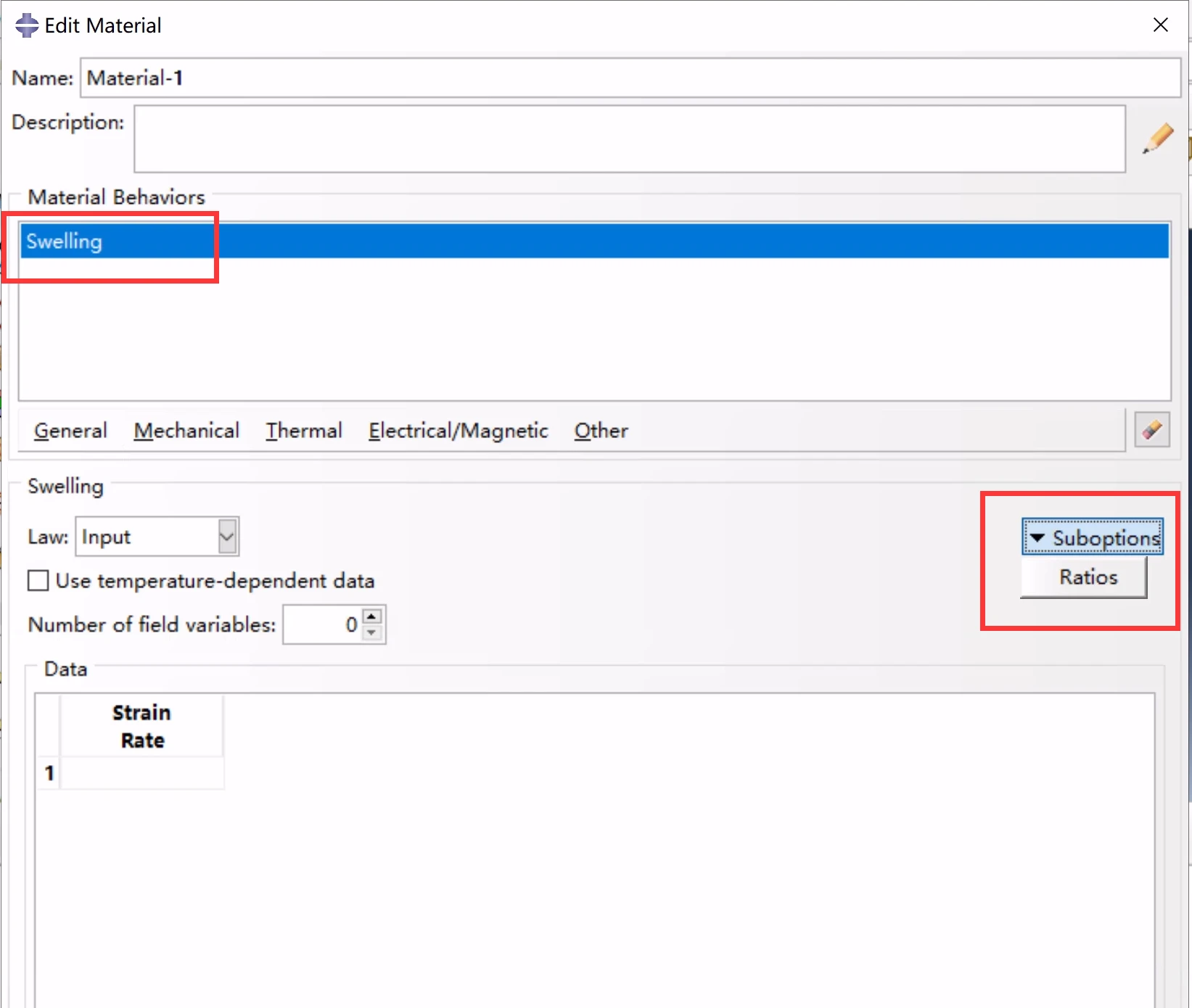
各向异性溶胀
Strain Rate:体积溶胀应变率
r11, r22, and r33:各向异性溶胀比 r11, r22, and r33
3. 用户子程序 CREEP
用户子程序CREEP为实现粘塑性模型(如蠕变和膨胀模型)提供了非常通用的能力,其中应变率势可以写成等效压应力p的函数;米塞斯或希尔等效偏应力,~q;以及任意数量的依赖于解的状态变量。解相关状态变量与本构定义一起使用,它们的值随着求解方案的变化而变化,并且可以在这个子例程中定义。例如与模型相关的强化变量。
用户子程序也可以用来定义通用的速率和时间相关的厚度方向垫片行为。当应变速率势需要更一般的形式时,可以使用用户子程序UMAT定义。
4. 在分析步骤中移除蠕变效应
可以指定在某些分析步骤中不发生蠕变(或粘弹性)响应,即使已经定义了蠕变(或粘弹性)材料特性。
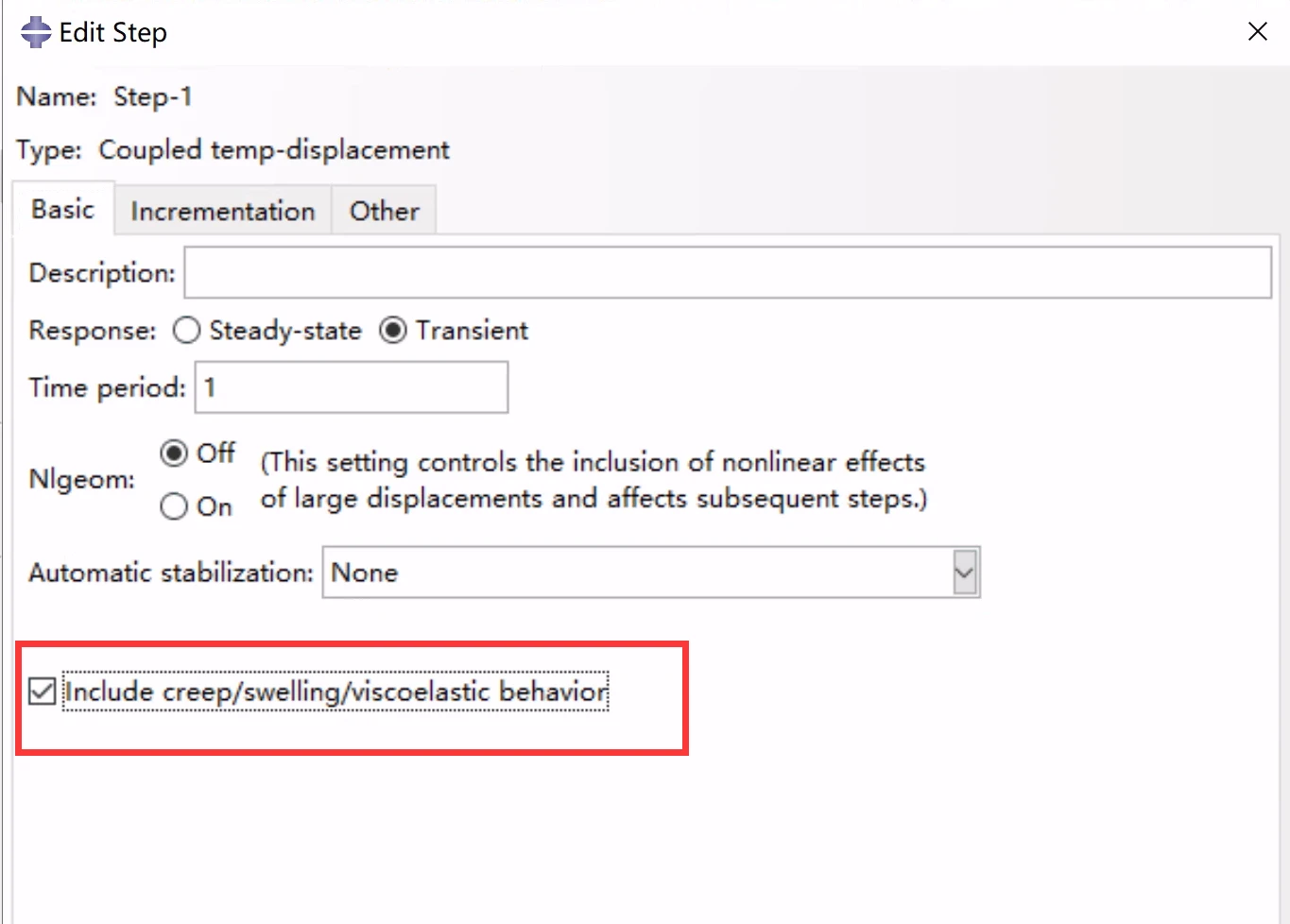
耦合的温度位移分析步中取消勾选
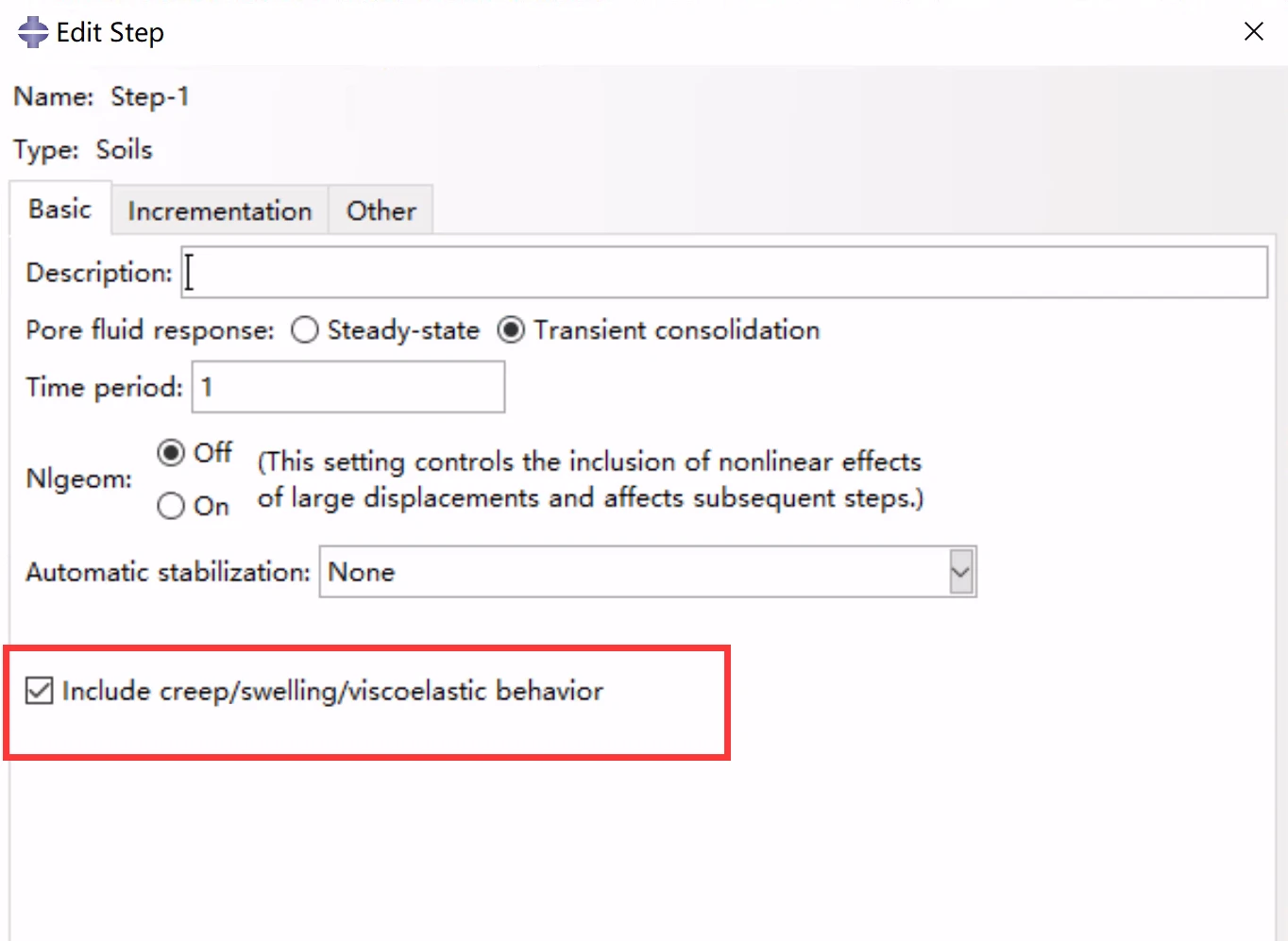
土壤:孔隙流体响应取消勾选
5. 积分
显式积分,隐式积分,或两种积分方案都可以用于蠕变分析,这取决于所使用的程序,为程序指定的参数,塑性的存在,以及是否要求几何非线性。
显式和隐式方案的应用
非线性蠕变问题通常采用非弹性应变的向前差分积分法(“初始应变法”)来求解。这种显式方法的计算效率很高,因为与隐式方法不同,它不需要迭代。虽然这种方法只是条件稳定的,但显式算子的数值稳定性极限通常足够大,可以在少量的时间增量内求解。
Abaqus/Standard使用显式或隐式集成方案,或者在同一步骤中从显式转换为隐式。首先概述这些方案,然后描述哪些程序使用这些集成方案。
方案1:从显式积分开始,根据稳定性(监测容差)或可塑性是否活跃,切换到隐式积分。
方案2:从显式积分开始,在可塑性活跃时转为隐式积分。稳定性判据在这里不起作用。
方案3:始终使用隐式积分。
上述积分方案的使用取决于求解类型、所选择的积分类型以及是否要求几何非线性。对于准静态和耦合温度-位移求解,如果不选择积分类型,则使用积分方案1进行几何线性分析,使用积分方案3进行几何非线性分析。当塑性在整个分析步中不活跃时(积分方案2),可以强制Abaqus/Standard对温度-位移耦合或准静态过程中的蠕变和溶胀效应使用显式积分。无论是否要求几何非线性,都可以使用显式积分。
对于瞬态土体固结过程,无论进行几何线性还是非线性分析,总是使用隐式积分方案(积分方案3)。
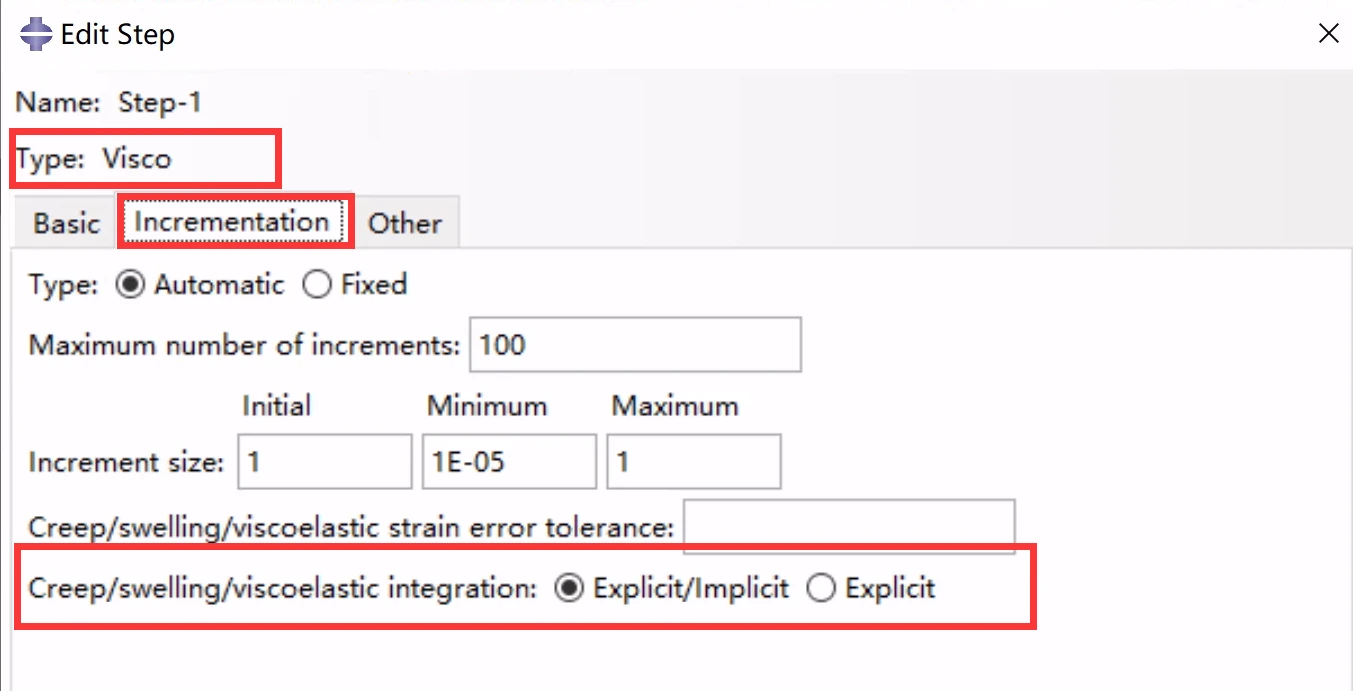
粘性分析步中
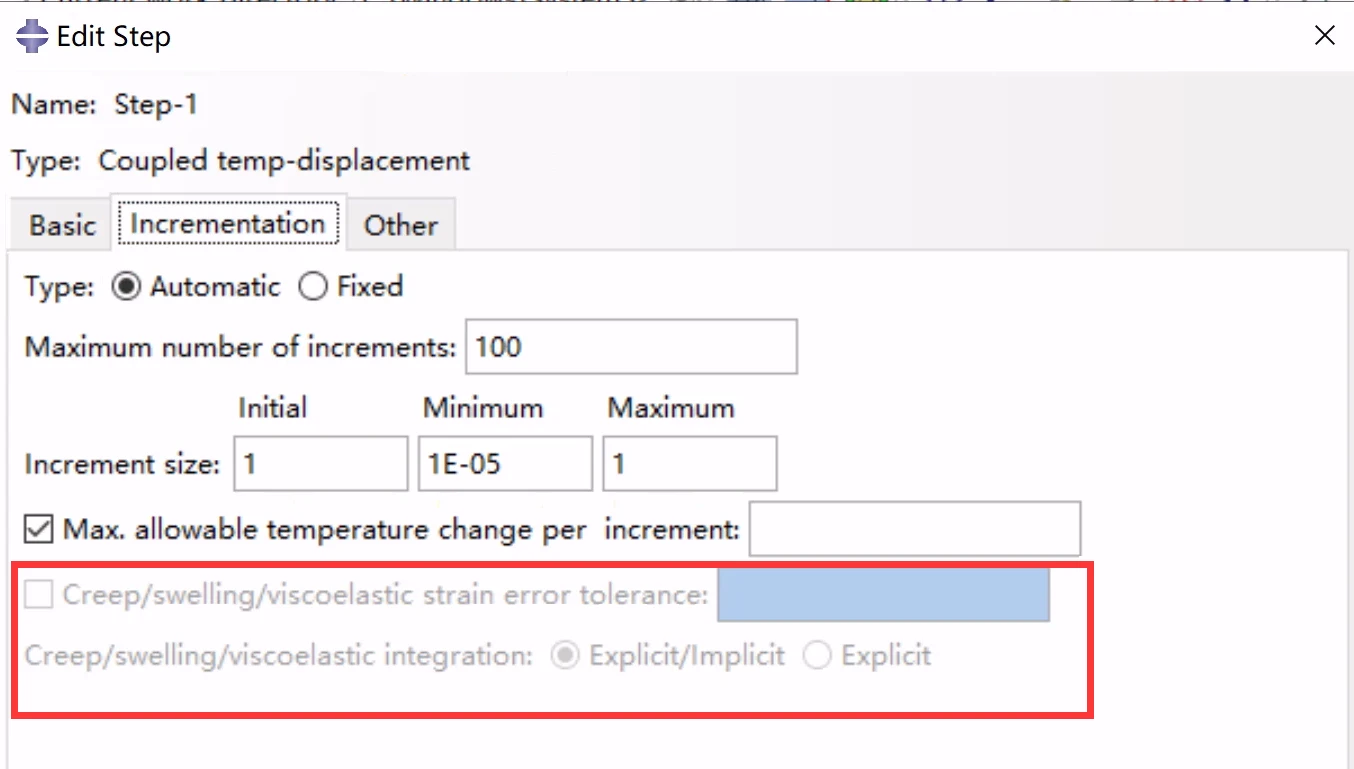
耦合的温度-位移分析步中
6. 用蠕变应变率控制加载
在Abaqus/CAE中不支持蠕变应变率控制。详细内容请参考帮助文档。
在超塑性成形中,施加可控压力使物体变形。超塑性材料可以变形到非常大的应变,只要变形的应变率保持在非常严格的公差范围内。超塑性分析的目的是预测如何控制压力以尽可能快地形成部件,而不超过材料中任何地方的超塑性应变率。
7. 单元和输出
率相关塑性(蠕变和溶胀行为)可用于Abaqus/Standard中具有位移自由度的任何连续体、壳体、膜、垫片和梁单元。蠕变也可以在任何垫片单元的厚度方向上定义,并结合垫片的行为定义。
除了Abaqus/ standard中可用的标准输出标识符之外,以下变量与蠕变和溶胀模型直接相关:
CEEQ: 等效蠕变应变
CESW:溶胀应变的大小
以下两个输出仅适用于蠕变应变率加载控制分析,在增量开始时输出,并在请求这些文件的任何输出时自动写入结果文件和输出数据库文件:
RATIO:等效蠕变应变率与目标蠕变应变率之比的最大值,r max
AMPCU:解相关振幅的当前值。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删