Abaqus材料属性定义：非弹性力学性能与各向异性屈服/蠕变

各向异性屈服和蠕变：

可用于在不同方向上表现出不同屈服和/或蠕变行为的材料；

是通过应用Hill势函数的自定义应力比引入的；

只能与金属塑性和在Abaqus/Standard中的金属蠕变材料模型结合使用；

可用于Abaqus/Explicit中非线性各向同性/随动硬化模型；

可以与Abaqus/Explicit中的渐进损伤失效模型结合使用，以指定不同的损伤起始标准和损伤演化规律，允许材料刚度的逐步退化和从网格中移除单元。

1. 屈服和蠕变应力比

各向异性屈服或蠕变行为是通过使用屈服或蠕变应力比Rij来模拟的。在各向异性屈服的情况下，屈服比是根据参考屈服应力σ0(由金属塑性定义给出)来定义的，因此，如果σ i j作为唯一的非零应力，则相应的屈服应力为Rij σ0。塑性流动法则定义如下:

在各向异性蠕变的情况下，R ij是计算蠕变应变率时用于衡量应力值的蠕变比。因此，如果σ 11是唯一的非零应力，则在用户定义的蠕变定律中使用的等效应力为~q = R 11 | σ 11 |。

屈服和蠕变应力比可以定义为常数或温度和预定义场变量的表格函数。必须使用局部取向来定义各向异性的方向。

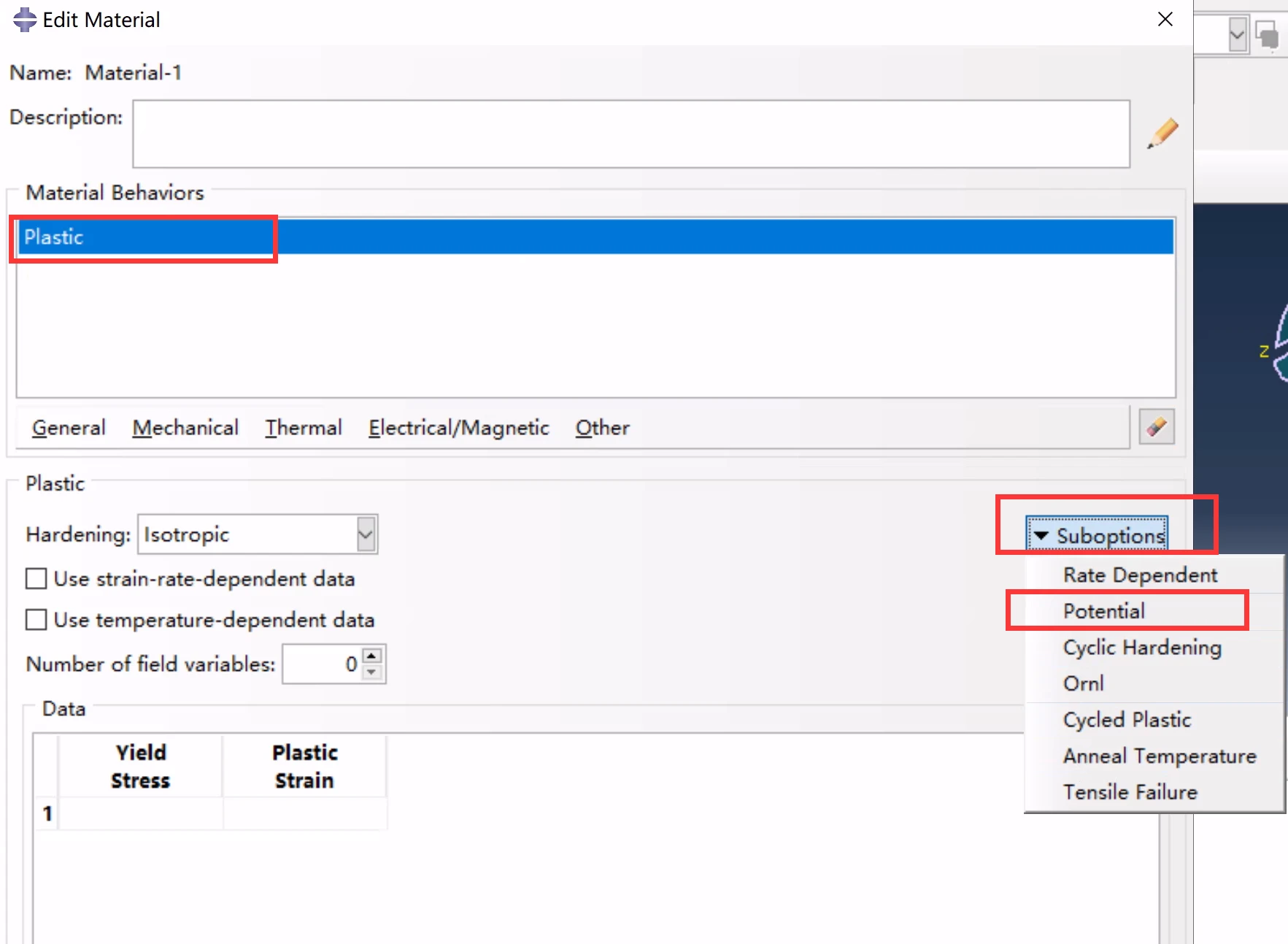
   各向异性塑性屈服的定义
 

   各向异性蠕变的定义
 

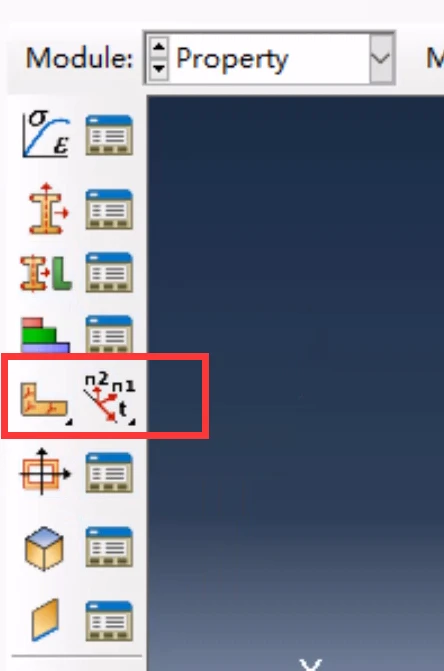
   材料取向定义
 

2. 各向异性屈服

Hill势函数是Mises函数的简单扩展，它可以用直角笛卡尔应力分量表示为

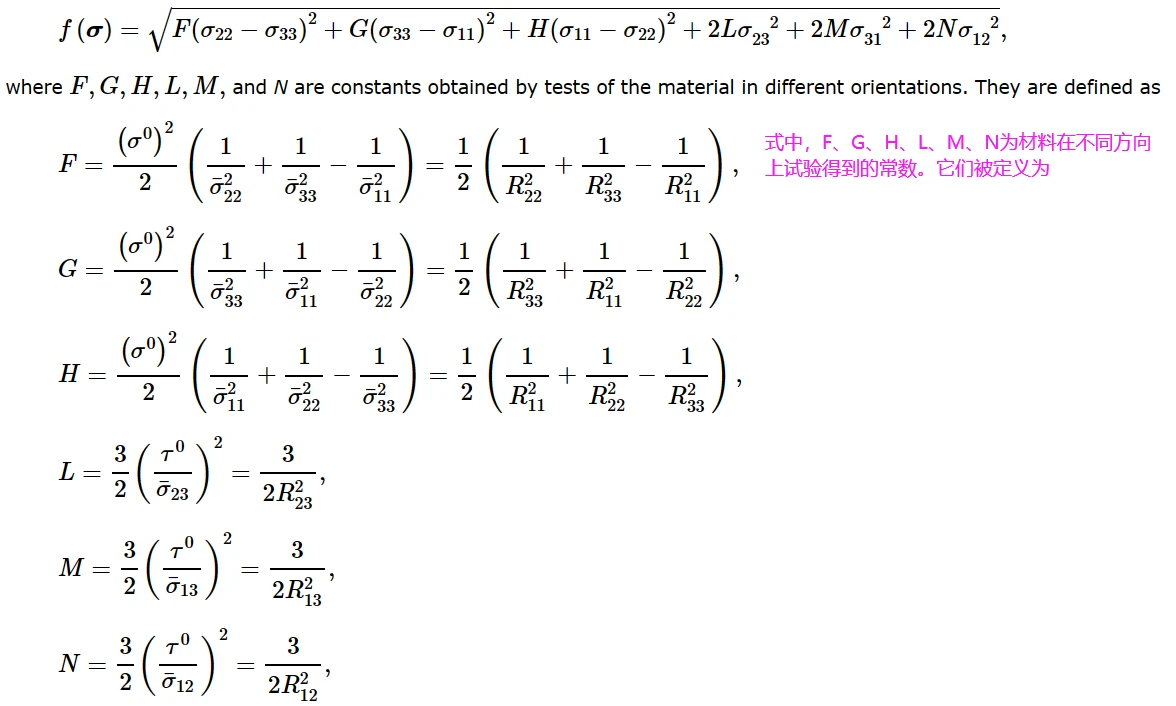
   Hill势函数
 

其中，当σ ij作为唯一的非零应力分量时，每个¯σ ij为测量的屈服应力值；σ 0为金属塑性定义中用户自定义的参考屈服应力；R11、R22、R33、R12、R13和R23为各向异性屈服应力比；τ 0 = σ 0 /√3。因此，六个屈服应力比的定义如下(按顺序)：

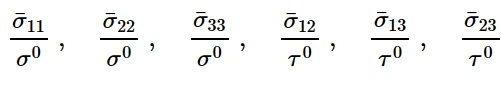
   屈服应力比的定义
 

由于屈服函数的形式，所有这些比率都必须是正的。如果常数F, G和H是正的，那么屈服函数总是很好定义。然而，如果这些常数中的一个或多个为负，则屈服函数对于某些应力状态可能是未定义的，因为平方根下的量是负的。

流动法则为：

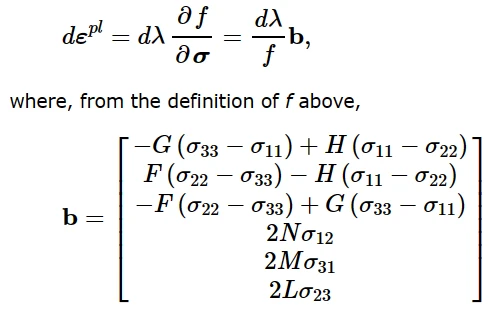
   流动法则的定义
 

3. 各向异性蠕变

对于各向异性蠕变，在Abaqus/Standard中，Hill函数可以表示为：

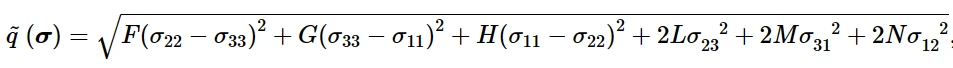
   各向异性蠕变时的Hill函数
 

式中，~q (σ)为等效应力，F、G、H、L、M、N为材料在不同方向上试验所得的常数，定义同上，与各向异性屈服相同的关系；然而，参考屈服应力σ 0被单轴等效偏应力~q（蠕变法则中）所取代，R11、R22、R33、R12、R13和R23被称为“各向异性蠕变应力比”。因此，6个蠕变应力比定义如下(按顺序排列):

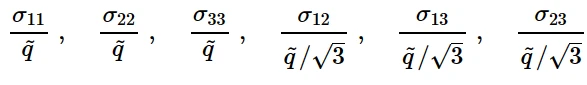
   蠕变应力比的定义
 

当计算蠕变应变率时，必须在每个方向上定义用于缩放应力值的比率R ij。若6个R ij值均为1，则得到各向同性蠕变。

4. 基于应变比定义各向异性屈服行为(Lankford's r-values)

如上所述，Hill的各向异性塑性势在Abaqus中由用户输入定义，由不同方向的屈服应力相对于参考应力的比值组成。然而，在某些情况下，例如钣金成形应用，通常会发现材料的各向异性数据是根据宽度应变与厚度应变的比率给出的。然后需要数学关系将应变比转换为可以输入Abaqus的应力比。

在钣金成形应用中，通常关心平面应力条件。考虑x, y为板材平面上的“纵rolling”和“横cross”方向; Z是厚度方向。从设计角度来看，通常期望的各向异性类型是板材在平面上是各向同性的，并且在厚度方向上具有增加的强度，这通常被称为横向各向异性。另一种各向异性的特征是在薄片平面的不同方向上强度不同，称为平面各向异性。

在薄板平面的x方向上进行简单的拉伸试验中，该势的流动规则(如上所述)将增量应变比(假设弹性应变较小)定义为：

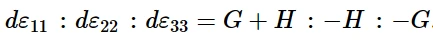
因此，通常称为Lankford r值的宽度与厚度应变之比为

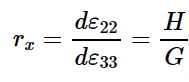
同样，对于薄板平面上y方向的简单拉伸试验，增量应变比为：

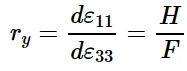
横向各向异性：

横向各向异性材料是指rx = ry的材料。如果将金属塑性模型中的σ 0定义为¯σ 11时：

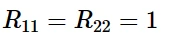
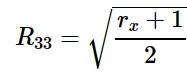
平面各向异性：

在平面各向异性的情况下，rx和ry不同，R11, R22, R33也不同。如果将金属塑性模型中的σ 0定义为¯σ 11时:

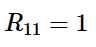
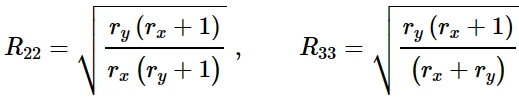
如果r x = r y = 1, R 22 = R 33 = 1，则变为了Mises各向同性塑性模型。

一般各向异性：

到目前为止，我们只考虑了沿各向异性轴施加的载荷。为了推导出平面应力的更一般的各向异性模型，板材必须在其平面上以另一个方向加载。假设我们做一个与x方向成α角的简单拉力试验;然后，从平衡考虑，我们可以把非零应力分量写成：

其中σ为施加的拉应力。将这些值代入流动方程，并假设弹性应变较小：

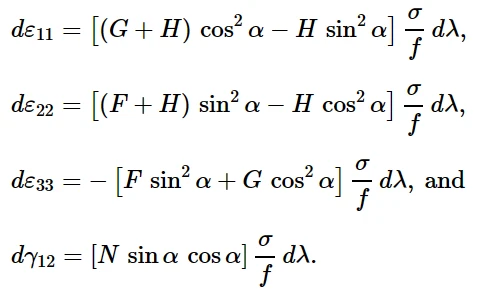
假设几何变化较小，则宽度应变增量(与加载方向成直角的应变增量α)为

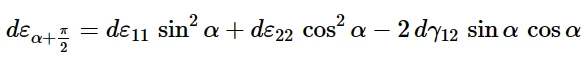
角度α加载的Lankford r值为：

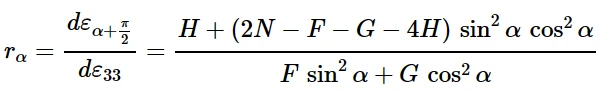
最常用的试验之一是加载方向为45°的试验。在这种情况下：

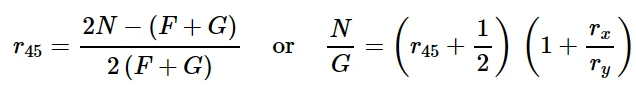
若在金属塑性模型中σ 0 =¯σ 11，则R 11 = 1。R22、R33与前面定义的横向或平面各向异性相同，利用上述关系:

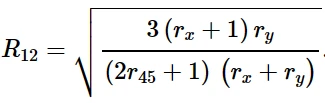
5. 渐进损伤与失效

在Abaqus中，显式各向异性屈服可以与关于延性金属的损伤和破坏中讨论的渐进损伤和失效模型结合使用。该功能允许指定一个或多个损伤起始标准，包括韧性、剪切、成形极限图(FLD)、成形极限应力图(FLSD)和<s:1>申伯恩-索恩成形极限图(MSFLD)标准。损伤发生后，材料刚度按照规定的损伤演化响应逐步退化。该模型提供了两种失效选择，包括由于结构撕裂而从网格中去除单元。渐进式损伤模型允许材料刚度的平滑退化，使其适用于准静态和动态情况。

   损伤起始准则
 

   并指定损伤演化规律
 

6. 初始条件

同各向同性屈服/蠕变的定义，若在各向异性屈服/蠕变材料研究时已经经过一些加工硬化行为时，Abaqus允许通过直接定义初始条件来指定等效塑性应变¯ε p1的初始条件。

7. 单元和输出

除了Abaqus/Explicit中的一维单元(梁和桁架)外，任何可以与Abaqus中的经典金属塑性模型一起使用的单元都可以定义各向异性屈服。在Abaqus/Standard中，它也可以定义为任何可以与线性随动硬化塑性模型一起使用的单元，但不能与非线性各向同性/随动硬化模型一起使用。同样，各向异性蠕变可以定义为任何单元，可以使用Abaqus/Standard中的经典金属蠕变模型。

当定义了各向异性屈服和蠕变时，Abaqus中可用的标准输出标识符以及与蠕变模型、经典金属塑性模型和线性随动硬化塑性模型相关的所有输出变量都是可用的。

定义各向异性屈服和蠕变时，下列变量具有特殊意义:

PEEQ：等效塑性应变

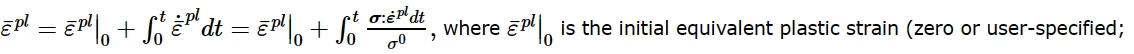
   PEEQ
 

CEEQ：等效蠕变应变

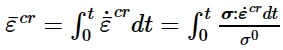
   CEEQ
 

YIELDS：屈服应力

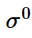
   YIELDS
 

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删