弹性力学性能-泡沫超弹性：Abaqus材料属性定义进阶

在超弹性这一小节包含：类橡胶材料的超弹性、弹性泡沫的超弹性、各向异性超弹性；

#弹性泡沫的超弹性

泡沫超弹性模型：

是各向同性和非线性的；

适用于孔隙度允许很大体积变化的多孔固体；

可指定能量耗散和应力软化效应；

可以弹性变形到大应变，高达90%的压缩应变；

要求在分析步骤中考虑几何非线性，因为它是用于有限应变应用。

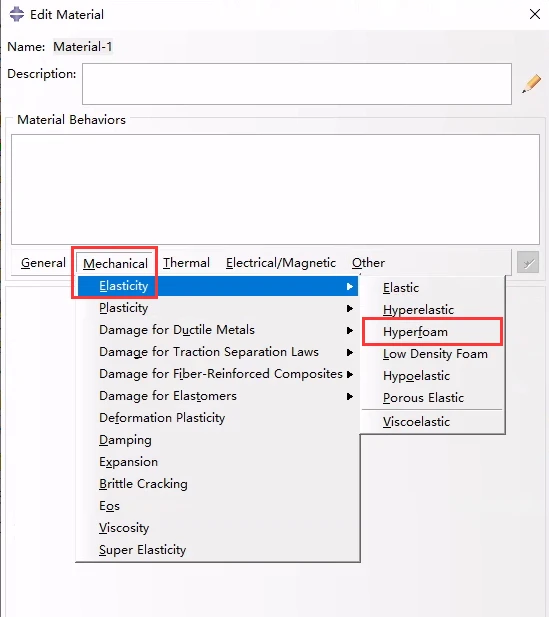
   超弹性泡沫
 

1.  弹性泡沫的力学性能

泡沫单胞可以是开放的(如海绵)或封闭的(如漂浮泡沫)。弹性体泡沫材料的常见例子是蜂窝聚合物，如坐垫、填充物和包装材料，它们利用泡沫的优异吸能特性：在一定应力水平下，泡沫吸收的能量远大于普通硬弹性材料吸收的能量。泡沫通常是压缩加载的。

下图呈现典型的压应力-应变曲线：

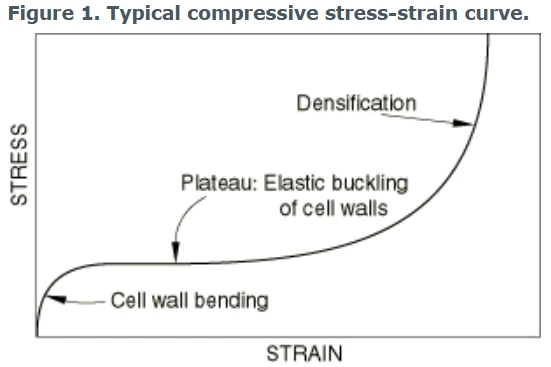
   弹性泡沫典型的压缩曲线
 

压缩过程可分为三个阶段：

①在小应变下(<5%)，泡沫由于单胞壁弯曲而以线弹性方式变形。

②几乎恒定的应力变形平台，这是由构成单胞边缘或壁的柱或板的弹性屈曲引起的。在闭孔中，封闭的气体压力和膜的拉伸增加了平台的水平和坡度。

③最后，致密化区域发生，单胞壁挤压在一起，导致压应力迅速增加。极限压缩标称应变为0.7至0.9。

下图显示了典型的拉伸应力-应变曲线：

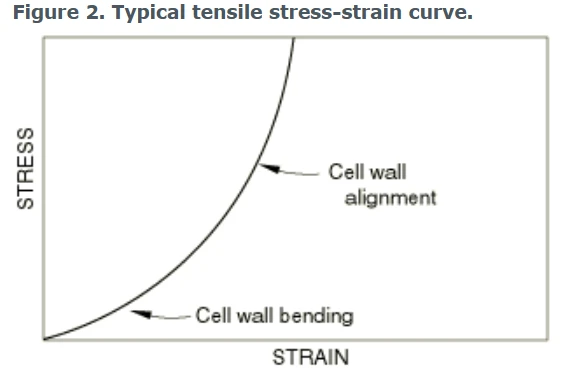
   弹性泡沫典型的拉伸曲线
 

拉伸有两个阶段：

①在小应变下，由于细胞壁弯曲，泡沫以线性弹性方式变形，类似于压缩时的变形。

②胞壁旋转并取向，导致刚度上升，进一步拉伸导致管壁轴向应变增加。

在压缩和拉伸的小应变下，实验观察到泡沫的平均泊松比ν为1/3。在较大的应变下，通常观察到压缩过程中的泊松比实际上为零:胞壁的屈曲不会导致任何显著的侧向变形；然而，在拉伸期间泊松比非零。

2. 定义超弹性泡沫行为：

泡沫超弹性材料的响应由应变能函数U中的参数定义;使用hyperfoam模型必须确定这些参数。材料参数的定义提供了两种方法:可以直接指定超泡材料参数（尽量通过材料评估将参数定义的材料行为与实验数据进行比较），也可以直接指定测试数据，让Abaqus计算材料参数。

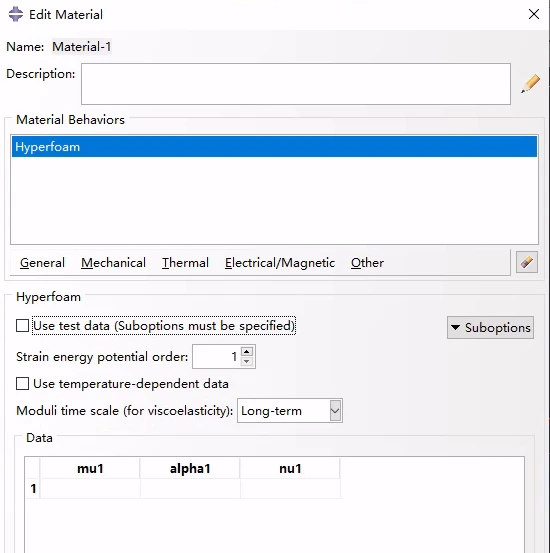
   直接给定参数
 

以上4个参数均是用于计算应变势能的必要参数：（说实话，这块没看懂，nu1对应β？）

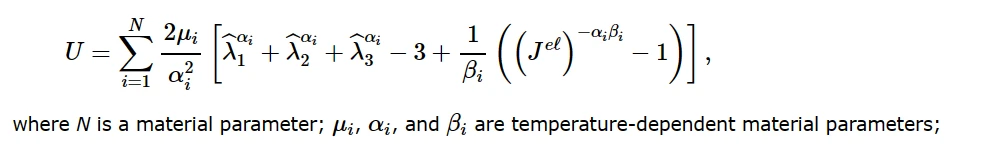
   应变势能
 

比较青睐使用实验数据直接拟合的方式：

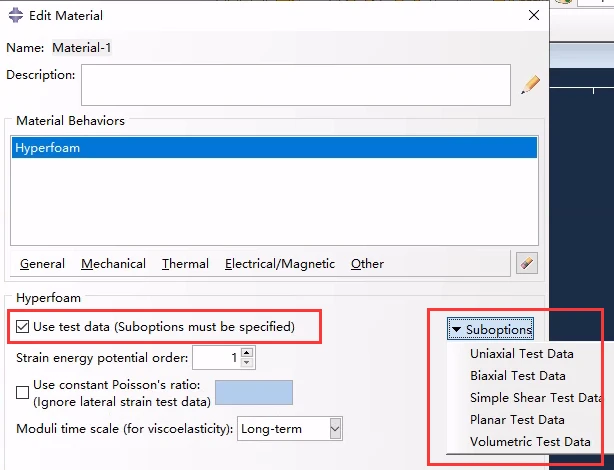
   指定实验数据
 

其他实验数据测试方法已在上节说明，简单剪切测试（纯剪切）如下：

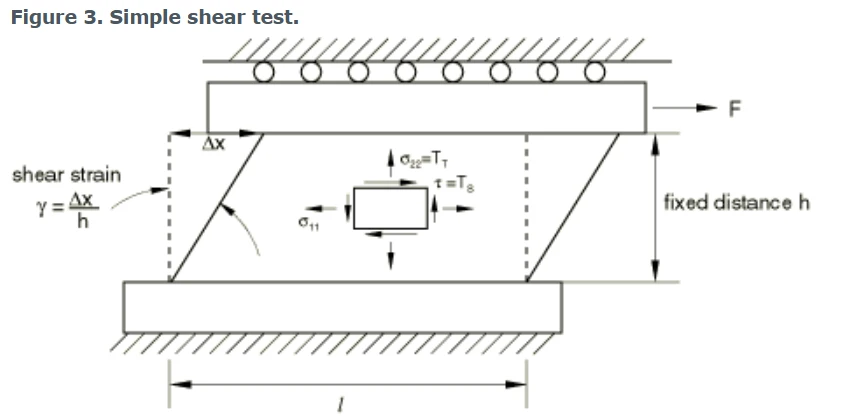
   简单剪切测试
 

体积压缩试验如下图。施加在泡沫试样上的压力为流体的静水压力，试样体积的减小等于新进入压力室的流体体积。试样密封，防止流体渗透。

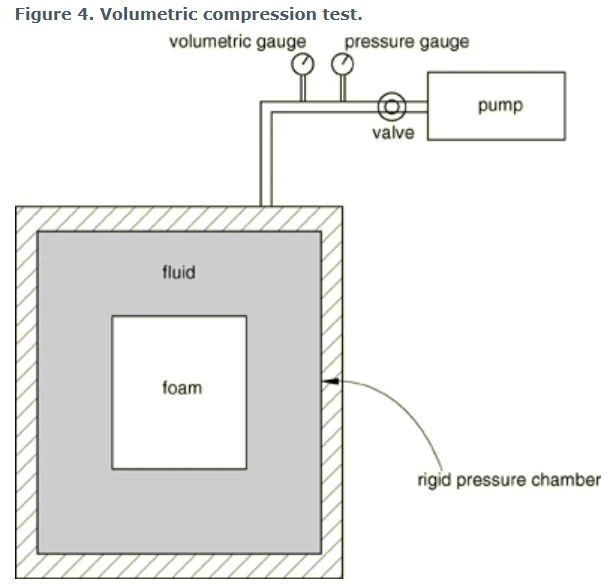
   泡沫的体积压缩实验
 

在大应变下，泡沫压缩(屈曲和破碎)和拉伸(对齐和拉伸)的变形机制不同。因此，精确的泡沫超弹性模型要求用于定义材料参数的实验数据与所分析问题的主要变形模式相对应。

如果压缩占主导地位，则相关测试为:单轴压缩、简单剪切（纯剪切）、平面压缩(泊松比不等于0)、 体积压缩(泊松比不等于0)；

如果拉伸占主导地位，相关的测试是: 单轴拉伸、简单剪切（纯剪切）、双轴拉伸(泊松比不等于0)、 平面拉伸(泊松比不等于0)；

横向应变数据也可以用来定义泡沫的可压缩性。侧向应变的测量可能使其他试验变得多余;例如，为单轴测试提供侧向应变消除了体积测试的需要。但是，如果在其他试验的侧应变数据之外还提供了体积试验数据，则在确定泡沫的可压缩性时将同时使用体积试验数据和侧应变数据。如果压缩比和张力比变化较大，则超泡沫模型可能无法准确拟合泊松比。

3. 单元适用性：

超弹性泡沫模型可用于固体(连续体)单元、有限应变壳(S4除外)和膜。但是，它不能用于一维实体单元(桁架和梁)，小应变壳(STRI3, STRI65, S4R5, S8R, S8R5, S9R5)或欧拉单元(EC3D8R和EC3D8RT)。

对于连续单元，弹性泡沫超弹性可以与纯位移公式单元一起使用，或者在Abaqus/Standard中与“混杂”(混合配方)单元一起使用。由于弹性泡沫被认为是非常可压缩的，使用混合单元通常不会比使用纯粹的基于位移的单元产生任何优势。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删