Abaqus材料属性定义进阶：弹性体损伤分析

类橡胶材料的永久变形：

用于建立实体弹性体和热塑性塑料的永久变形；

基于变形梯度的乘法分解；

基于不可压缩各向同性硬化塑性理论；

可用于任何各向同性超弹性模型；

可与Mullinus effect相结合；

不能用于模拟粘弹性或滞后效应或与稳态传输求解。

1. 材料的行为

实体橡胶弹性体在循环加载条件下的真实行为非常复杂，如图1所示。

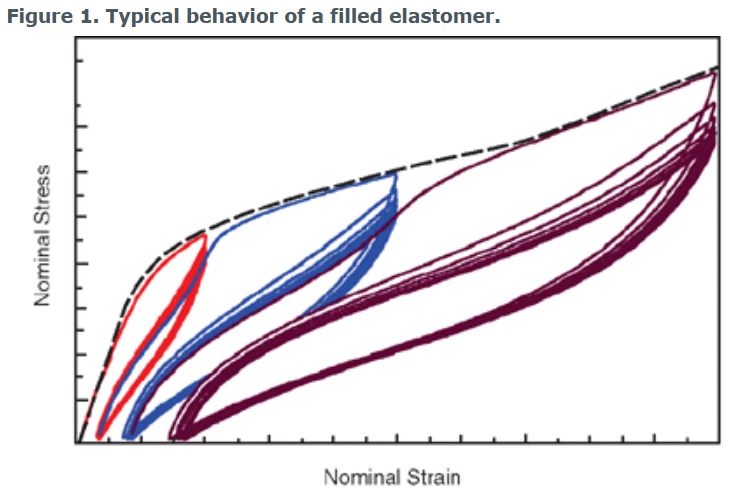
   图1 实体橡胶弹性体的真实循环加卸载曲线
 

材料发生渐进式损伤（每次循环的应力逐渐降低）、应力软化(也称为穆林斯效应Mullinus effect)、能量的滞回耗散以及永久变形。本节是关于永久变形的建模。

2. 理想的材料行为

从图1中可以清楚地看出，永久变形对于每个循环都是不同的，但是材料在零应力和给定应变水平之间的加载循环之后有稳定的趋势。对于图1中虚线所示的主加载路径上的给定加载水平，理想的永久变形将是卸载后具有单个应变值。

永久变形行为通过具有关联流动法则的各向同性硬化Mises塑性模型建立。在与底层橡胶样材料相关的有限弹性应变的背景下，塑性是使用变形梯度的乘法分解成弹性和塑性分裂来建模的：

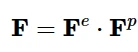
   式中，Fe为变形梯度的弹性部分(表示超弹性行为)，Fp为变形梯度的塑性部分(表示无应力中间构型)。
 

3. 定义永久变形---Plastic-Isotropic

初始超弹性行为可以用任何超弹性材料模型来定义；如果使用测试数据输入作为定义材料超弹性响应的方式，则必须指定卸载发生后的无应力中间构型。

永久变形可以通过屈服应力和等效塑性应变的各向同性硬化函数来定义。在这种情况下，屈服应力是发生卸载的主加载路径上的(有效)基尔霍夫应力，等效塑性应变是在材料中观察到的相应的对数永久变形。如果σ为真(柯西)应力，则基尔霍夫应力定义为Jσ，其中J为F的行列式。

根据所建模的内容，永久变形可以定义为粘弹性应变恢复后的真实永久变形，也可以包含粘弹性应变。无论是哪一种情况，都需要定义一个初始屈服应力，低于此应力将不会有永久变形，材料的行为将是完全弹性的。对于实体橡胶，这个初始屈服应力可能对应于一个小的非零应力；而对于热塑性材料族，初始屈服应力可能有一个更大的值。

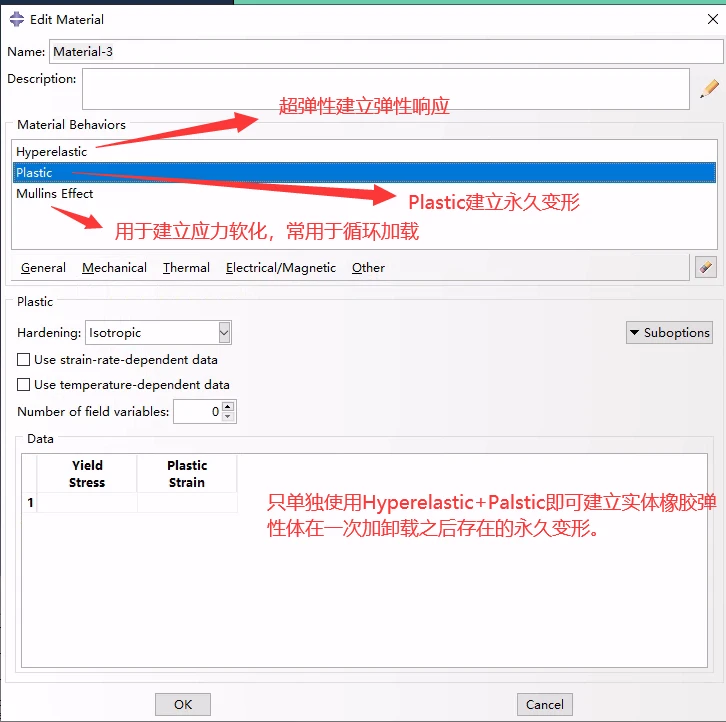
   CAE的建立
 

Abaqus具有可以通过单轴或双轴的测试数据得到材料超弹性，塑性和穆林斯效应的插件

4. 局限性，单元和求解

该模型旨在捕获多轴应力状态和轻度反向加载条件下的永久变形。这个模型不能用于捕捉完全反向加载下的变形。任何速率效应只适用于材料定义的塑性部分。

可以用于支持使用超弹性材料模型的所有单元类型。

永久变形建模可以在支持使用超弹性材料模型的所有求解器中进行（除稳态传输求解）。在Abaqus/Standard中的线性摄动分析步中，采用弹性部分对应的当前材料切线刚度来确定响应，而忽略任何塑性影响。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删