具有Mullins效应和永久变形的实体圆盘分析
这个例子将说明使用mullinus效应模拟固体橡胶盘和刚性表面之间的静态和稳态滚动的相互作用。将Mullins效应与超弹性材料模型结合,对实体弹性体在一定变形水平下卸载时的应力软化现象进行了模拟。这个例子还包括永久变形的建模。(本例子可以在abaqus帮助文档Analysis of a solid disc with Mullins effect and permanent set部分找到)
1. 问题描述
这个例子分为三个部分。第一部分涉及实验数据的校准,以确定穆林斯效应的材料系数。第二部分描述了固体圆盘在与代表道路的平面刚性表面接触引起的循环变形的静态响应。第三部分是第二部分问题的延续,研究了变形圆盘的滚动解。该实例还说明了Abaqus增强的沙漏控制能力和永久变形的建模。本节我们重点关注第一部分,材料参数的定义,即数据的校准!
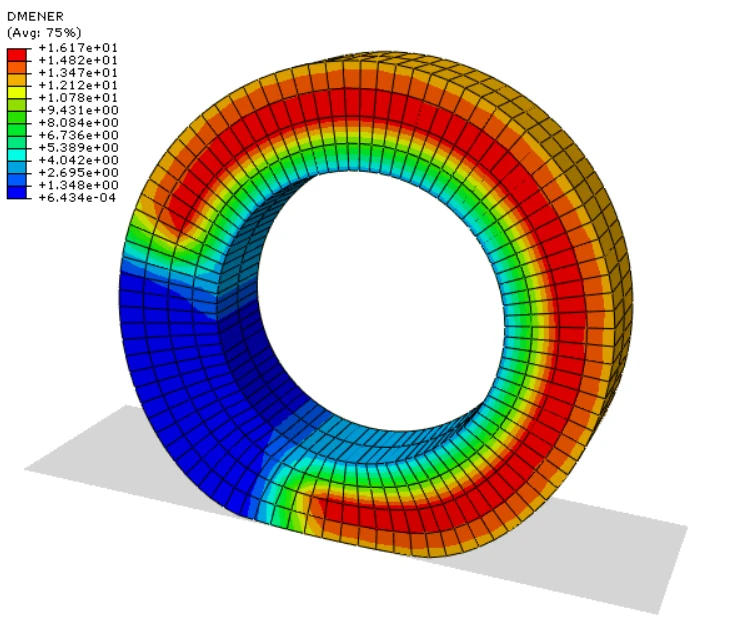
实体圆盘分析
2. 材料性能的校准
使用Mullins效应材料模型的第一步是校准测试数据。图1显示了实体橡胶的一组典型单轴拉伸实验数据。
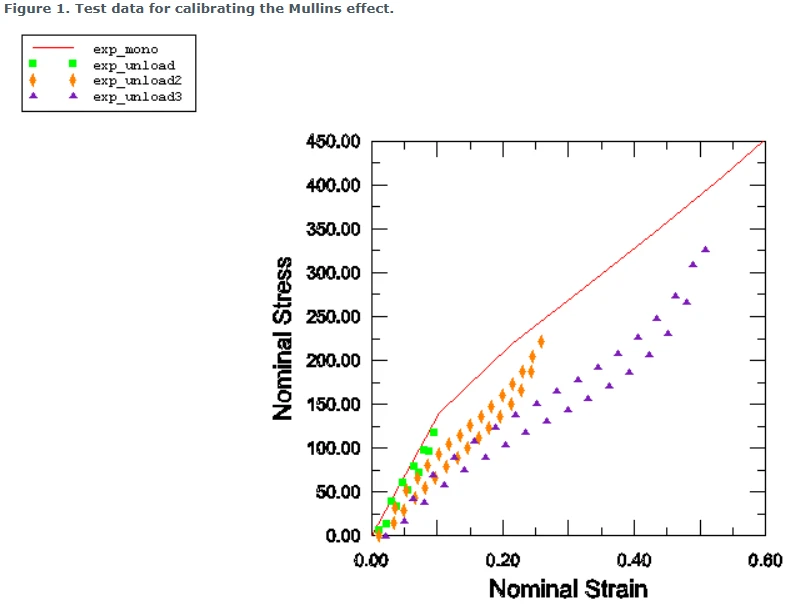
图1 用于校准的实验数据
其中,标注为exp_mono的曲线表示橡胶材料单调加载得到的初始行为。这组数据通过自定义超弹性材料模型提供单轴测试数据给Abaqus计算超弹性材料常数。在本例中,采用Yeoh材料模型校准材料的主行为,如图2。
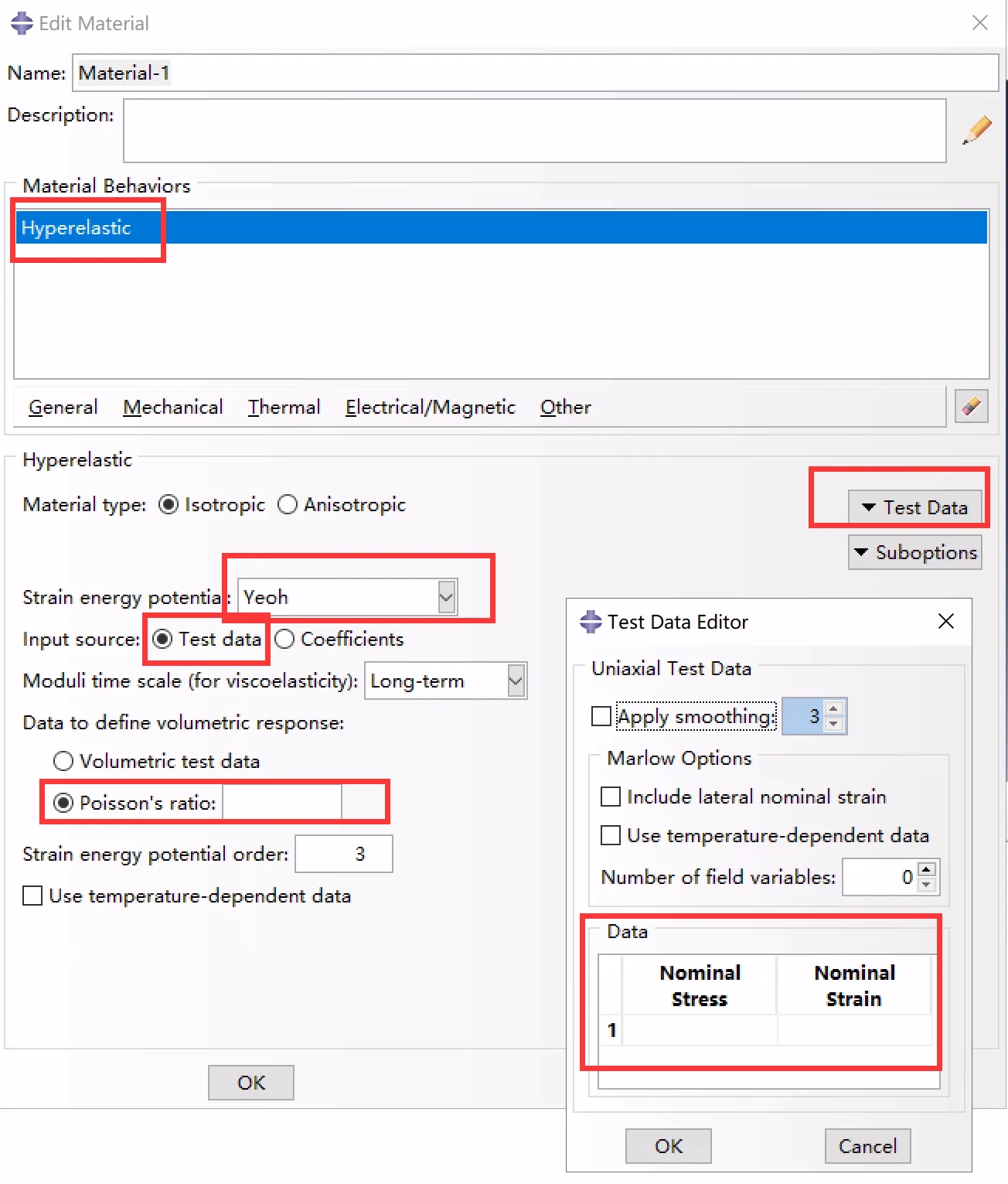
超弹性模型定义材料初始行为
另外,图1中卸载-再加载数据用于校准Mullins效应系数,作为三组不同最大应变水平的稳定加载/卸载循环数据提供。虽然在每个最大应变水平下用于Abaqus计算Mullins效应模型预测的卸载和再加载为单一曲线,但实际材料通常表现为循环行为。在给定应变水平下的卸载/再加载循环在前几个循环中表现出渐进损伤,经过几个周期后趋于稳定。因此,卸载-再加载数据可以以几个应变水平下所有加载/卸载循环的数据点形式提供给Abaqus(每个应变水平下提供多组卸载加载曲线),也可以仅以几个应变水平下的一组已稳定循环的数据点形式提供给Abaqus(每个应变水平线下仅提供循环稳定后的卸载加载曲线)。
在本例中,之所以选择稳定循环,是因为所考虑的结构预计会经历反复的循环荷载。标记为exp_unload1、exp_unload2和exp_unload3的曲线分别代表最大名义应变水平为0.099、0.26和0.51时的稳定卸载/再加载周期。上述三组卸-加载试验数据(每个最大应变水平为一组)通过Mullins效应的试验数据定义方法输入。
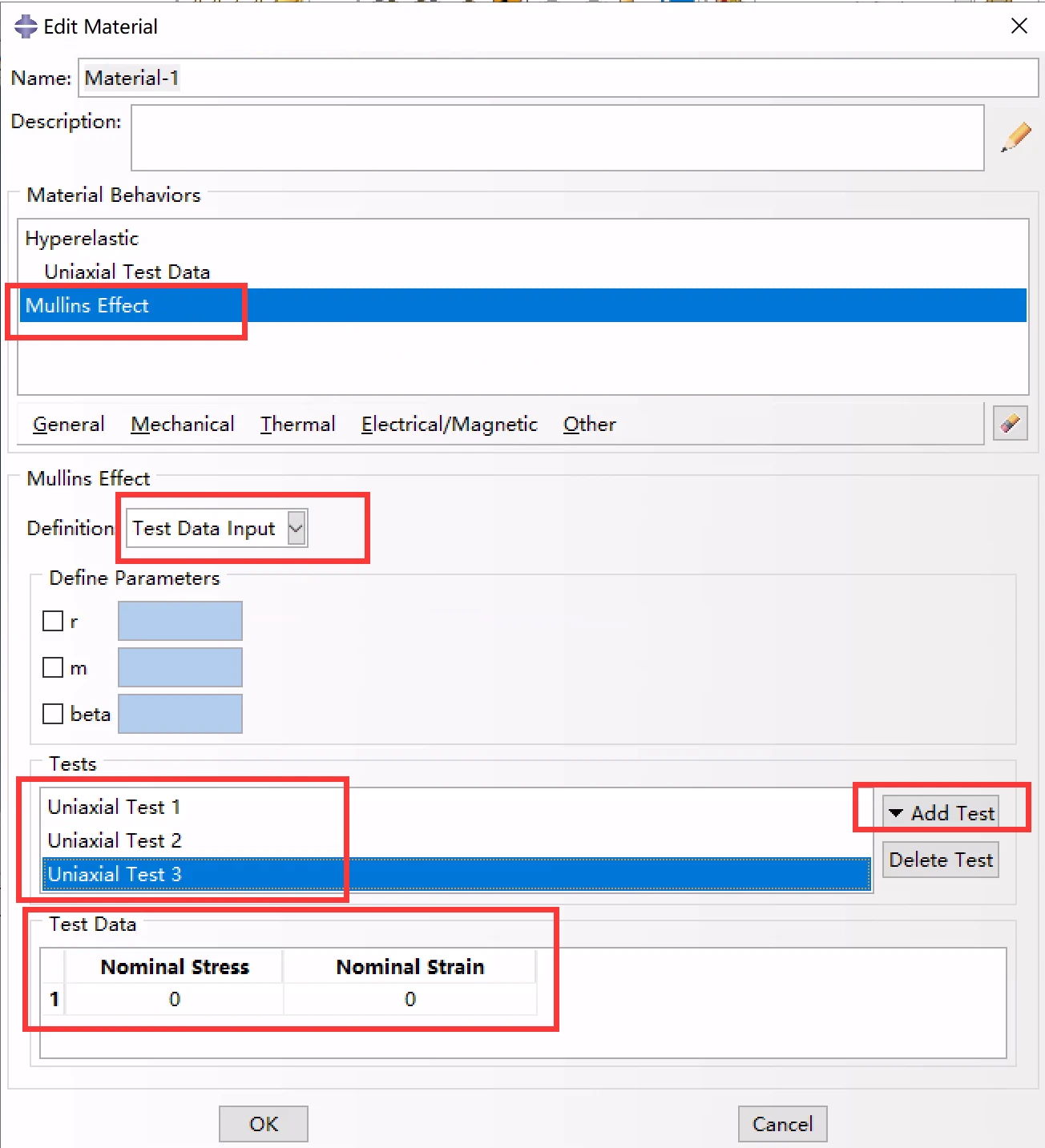
给出拟合mullinus效应的三组卸载加载实验数据
对于包含永久变形的模型,应使用金属塑性材料拟合数据,以便在加载中获得更柔和的响应(与纯超弹性材料相比)。同样应与Mullins效应结合;
另外,分析人员可以使用稳定周期的加载部分、稳定周期的卸载部分或两者的平均值来校准穆林斯效应参数。在这个例子中,考虑循环加载而不是初始的单调加载,因此卸载和重加载数据都被用于校准,即研究的是平均行为。
图2显示了Abaqus的对实验数据的校准响应。其中连续的蓝绿色曲线即为abauqs对提供试验数据的三个最大应变水平下的循环加卸载的数值响应。如图所示,Abaqus用一条曲线近似每个应变水平上的稳定周期,且在任何应变水平下该模型都不能捕捉到前几个循环过程中的渐进损伤。
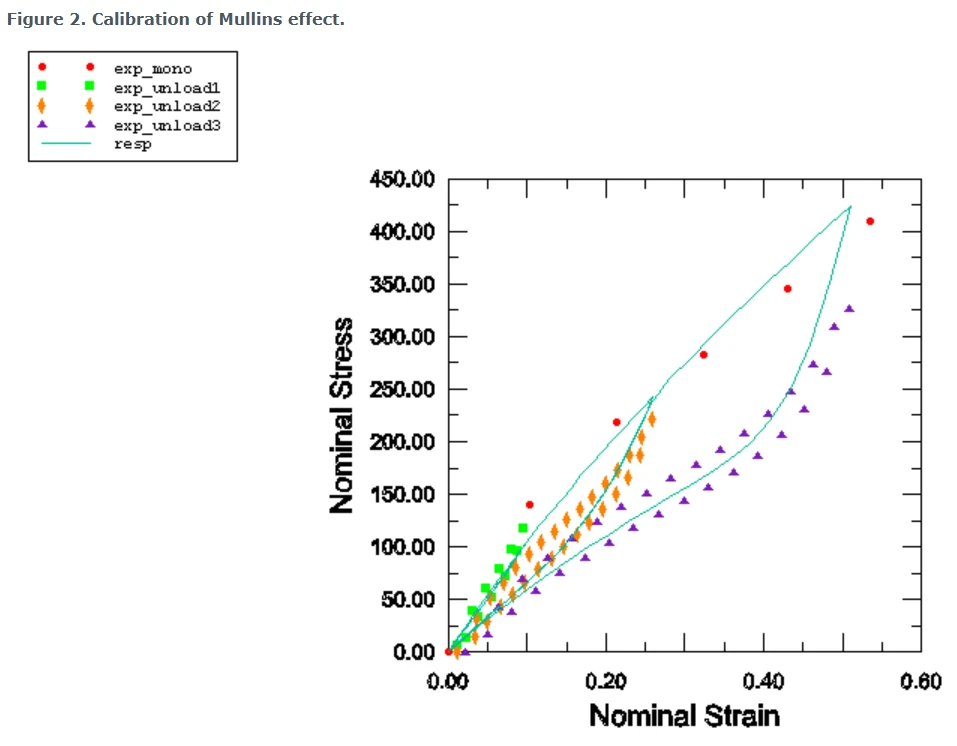
图2 Millus效应的校准响应
数值响应结果既可以通过进行单轴加载/卸载试验得到。或者,可以通过使用模型定义数据请求并简单地执行数据检查运行来获得初始行为和卸载-重新加载行为的数值响应。在后一种情况下,Abaqus计算的响应与实验数据一起输出到数据(.dat)文件中。这些数据可以在Abaqus/CAE中绘制,以进行比较和评估。材料的初始行为也可以用Abaqus/CAE中提供的自动化材料评估工具进行评估。
数据检查
材料评估材料的初始行为(超弹性模型):
材料评估
通过以上步骤我们即完成了材料属性的定义,或者通过数值响应结果得到材料行为参数,并使用直接给定参数的形式重新定义材料。
3. 实例操作步骤:
打开abaqus,修改工作路径后,保存CAE,建立一个实体长方体杆(5*5*20,你也可以用别的尺寸):
建立3D solid部件
然后定义材料:① 建立超弹性模型,使用Yeoh应变势能,通过指定测试数据的方式,给出单轴实验数据,将第一部分的数据复制过来(在文末给出),最后给定泊松比0.3:
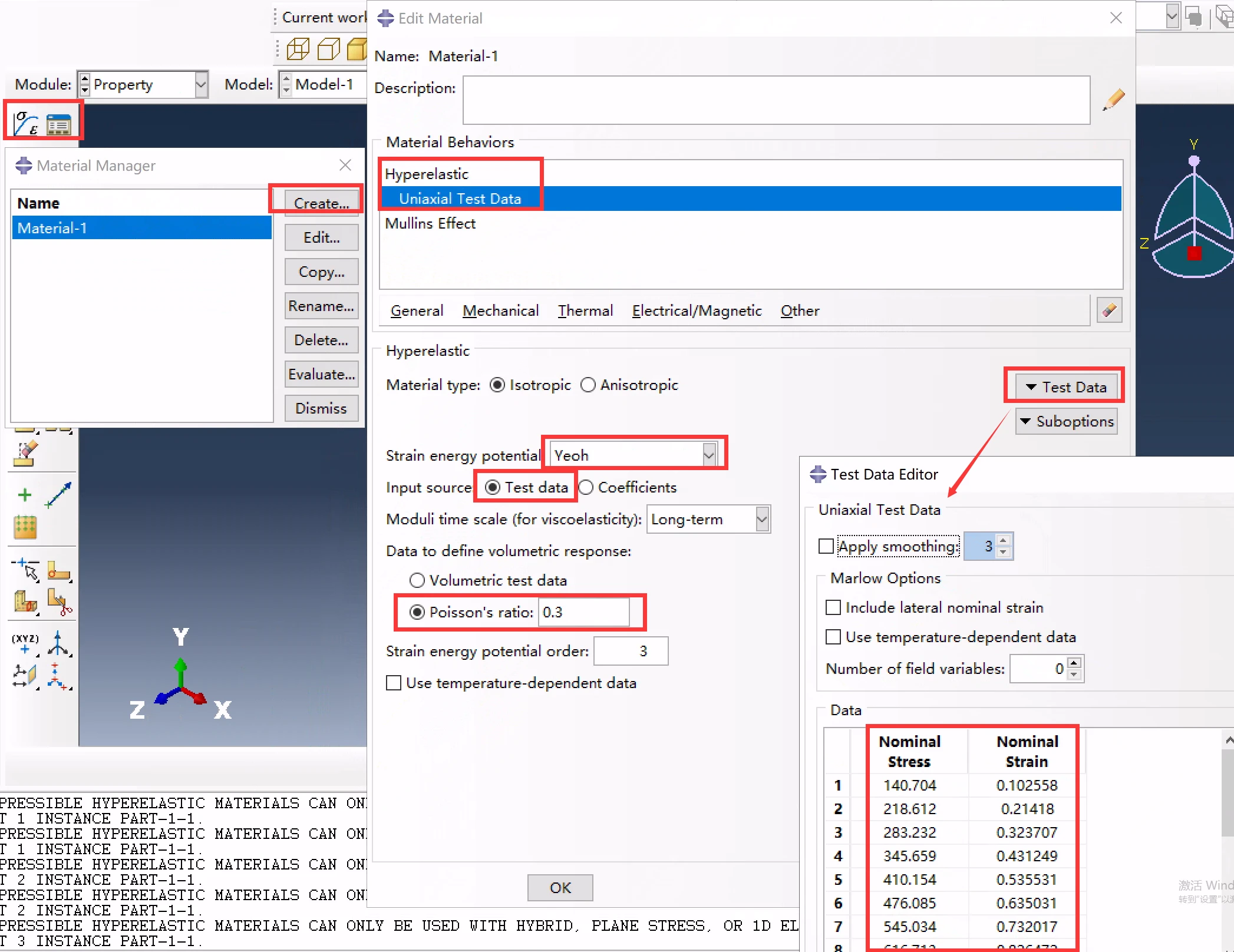
首先定义超弹性模型
②定义mullinus effect,选择通过实验数据输入的方式,添加三组单轴实验,并在每个测试数据下分别粘贴文末给出的3组测试数据:
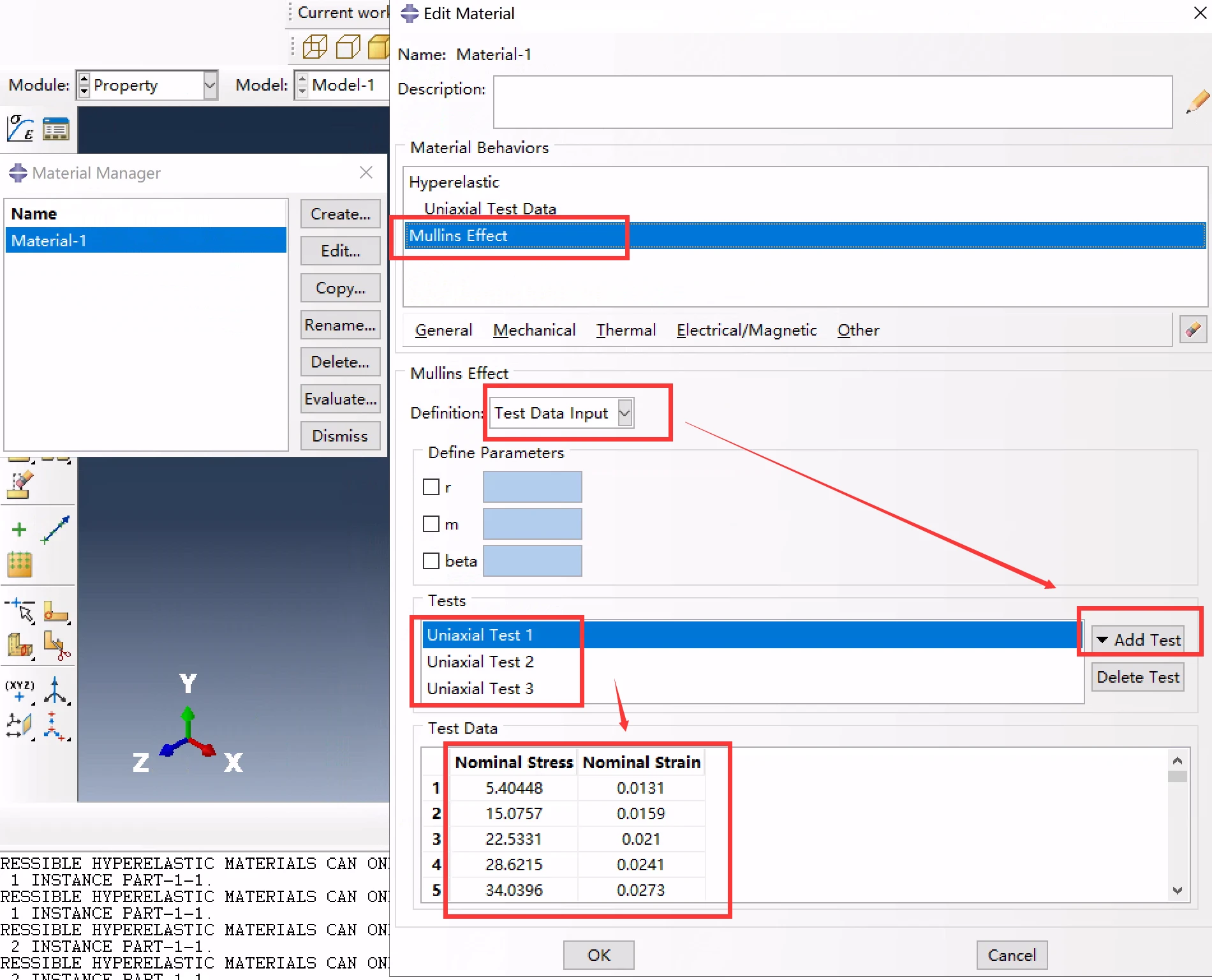
定义mullinus效应
评估超弹性模型:
材料评估超弹性行为
对刚刚建立的材料进行评估,设置好后ok自动计算:
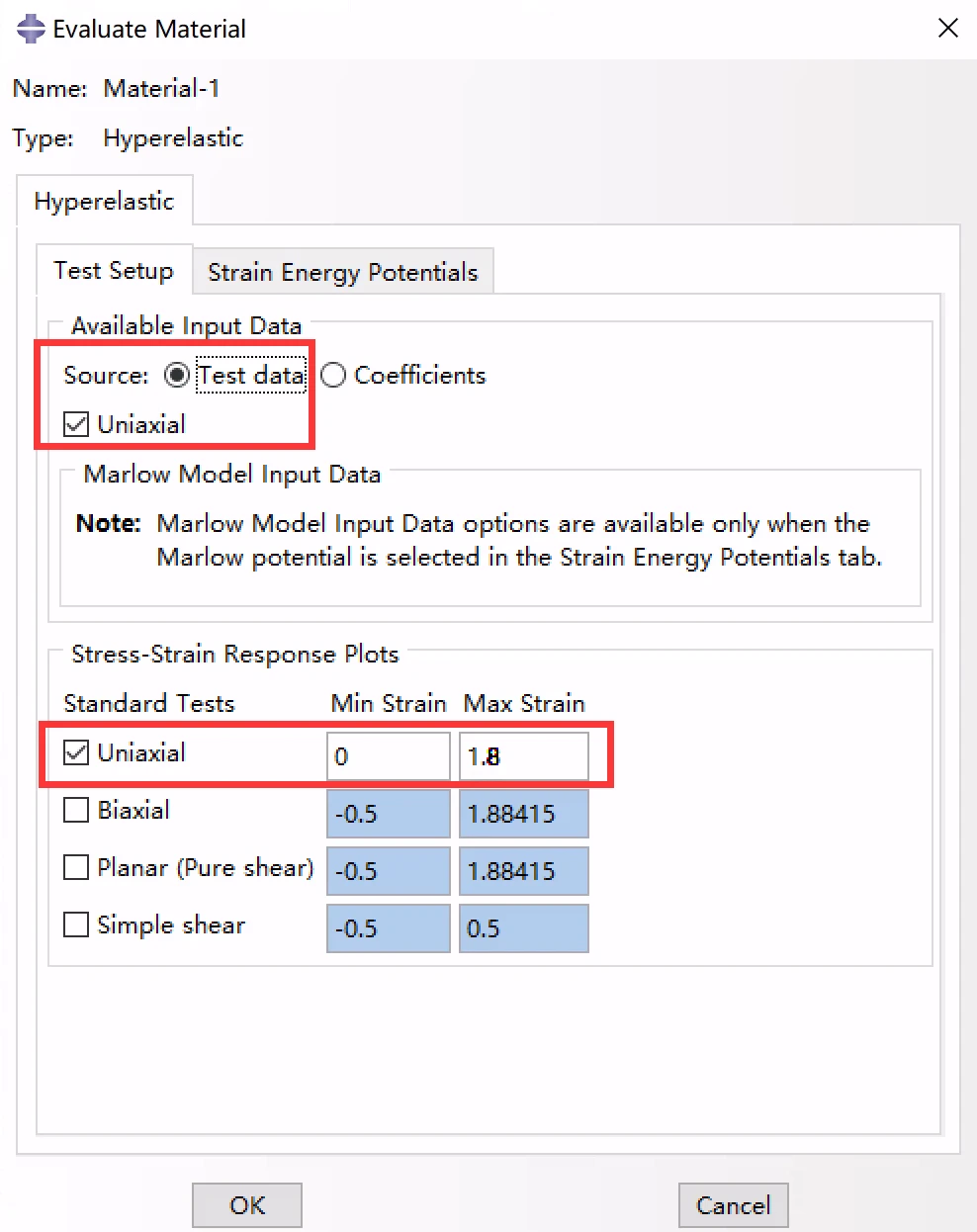
材料评估数据设置页
应变能选用Yeoh:

材料评估应变能选择页
自动计算结果:

拟合结果
可见,采用Yeoh模型对材料超弹性数据拟合良好,;
接下来,对部件进行加卸载,计算分析得到的应力数据与实验的加卸载数据进行比较,以验证mullinus效应:
材料设置好后,建立相应的均质实体截面,并赋予部件;
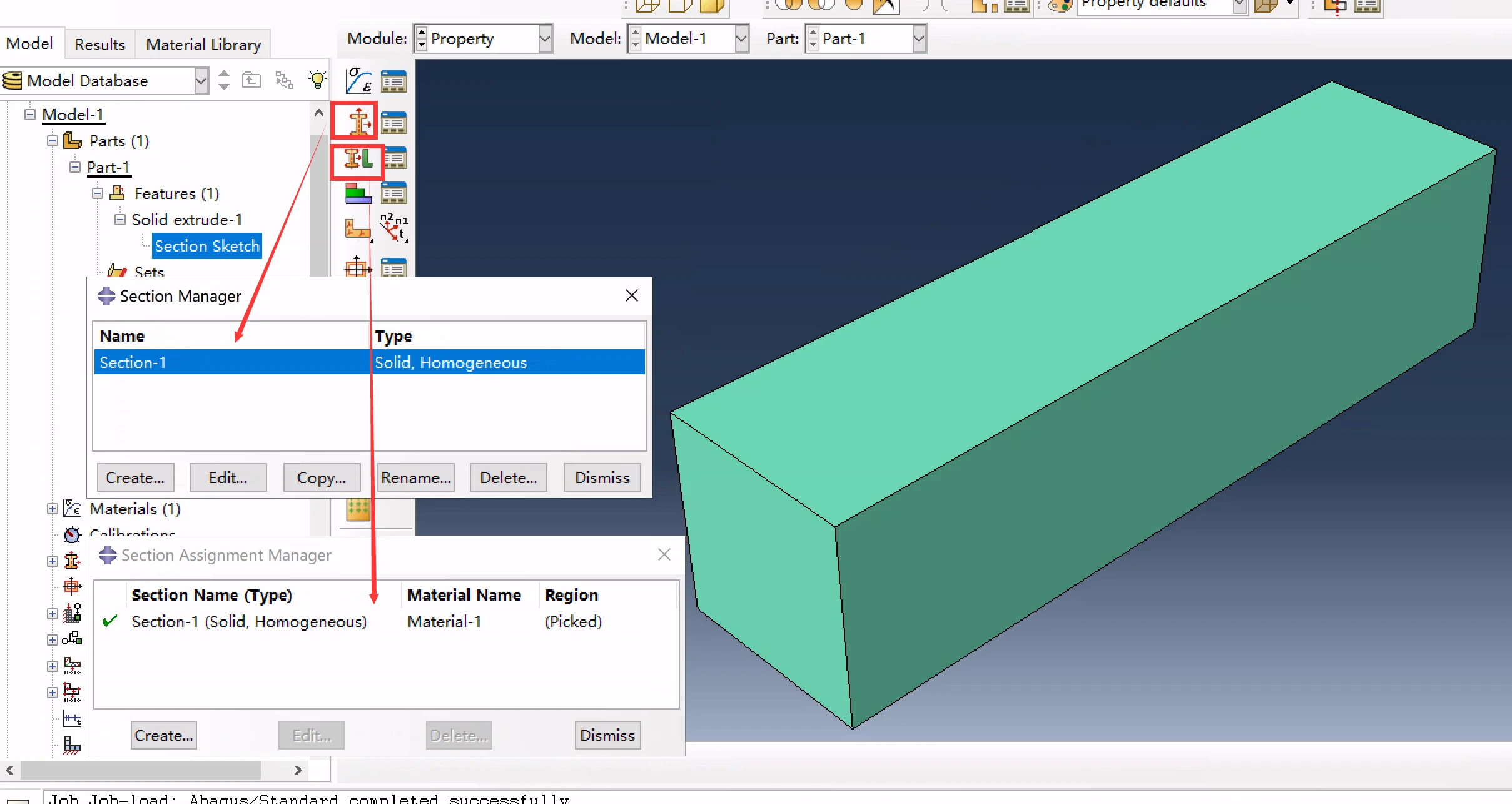
设置截面,赋予部件材料属性
导入装配体:
装配图
建立6个静力通用分析步,打开几何非线性,初始增量步设为了0.1(习惯给小一点了,没试默认情况,大家可自行尝试)
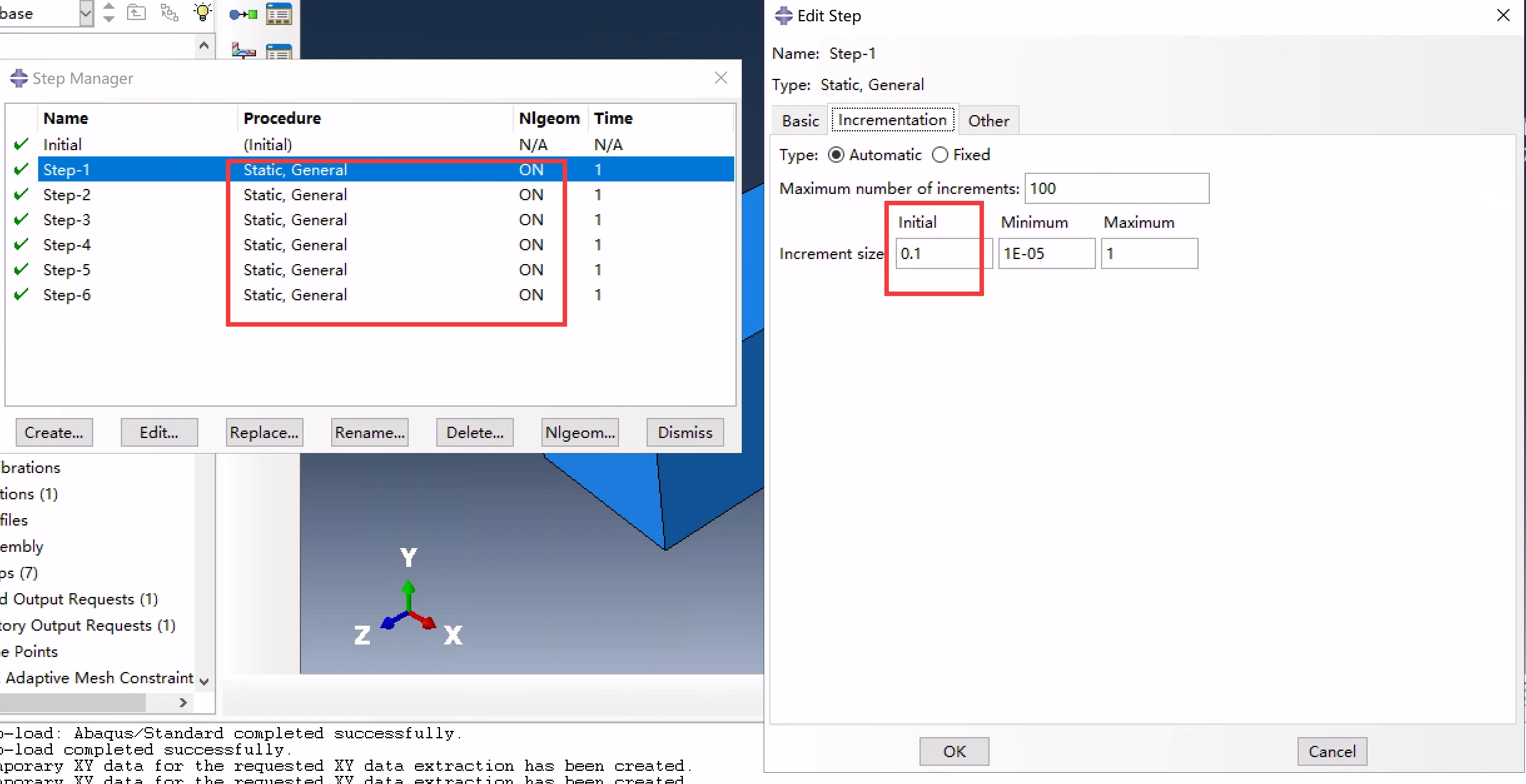
设置分析步
因为只有一个部件,所以不必设置相互作用,进入载荷模块:
一端面完全固定:

完全固定
另一端面给定位移约束:

位移约束
修改后续分析步的U3位移,分析步1为1.95,分析步2为0,分析步3为5.2,分析步4为0,分析步5为10.2,分析步6为0:
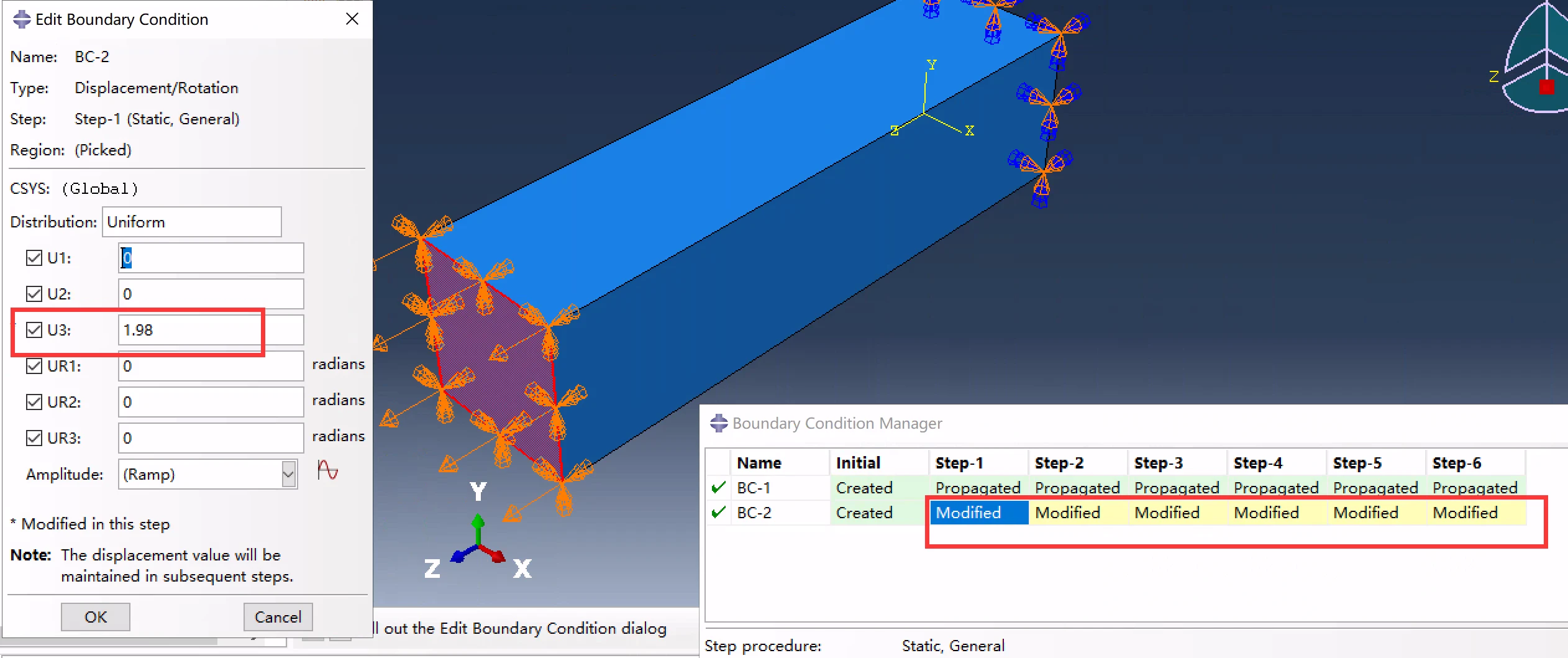
修改分析步U3
然后进行网格划分:
网格划分
建立Job进行计算:
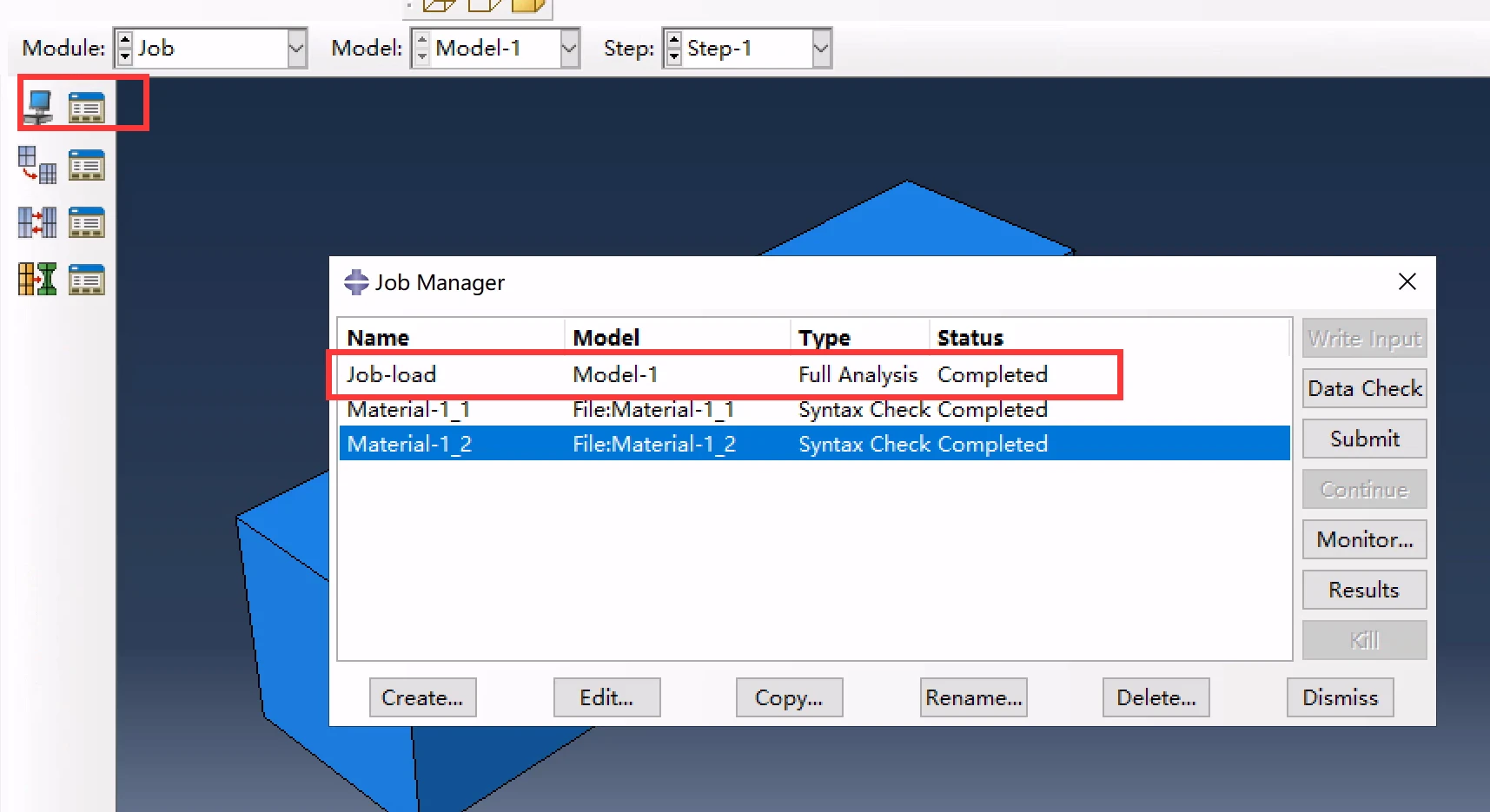
Job计算
后处理查看计算结果:
然后输出场变量应力随时间的变化,并保持为数据S33:

应力随时间的变化
端面位移随时间的变化曲线,并保存为数据U3:
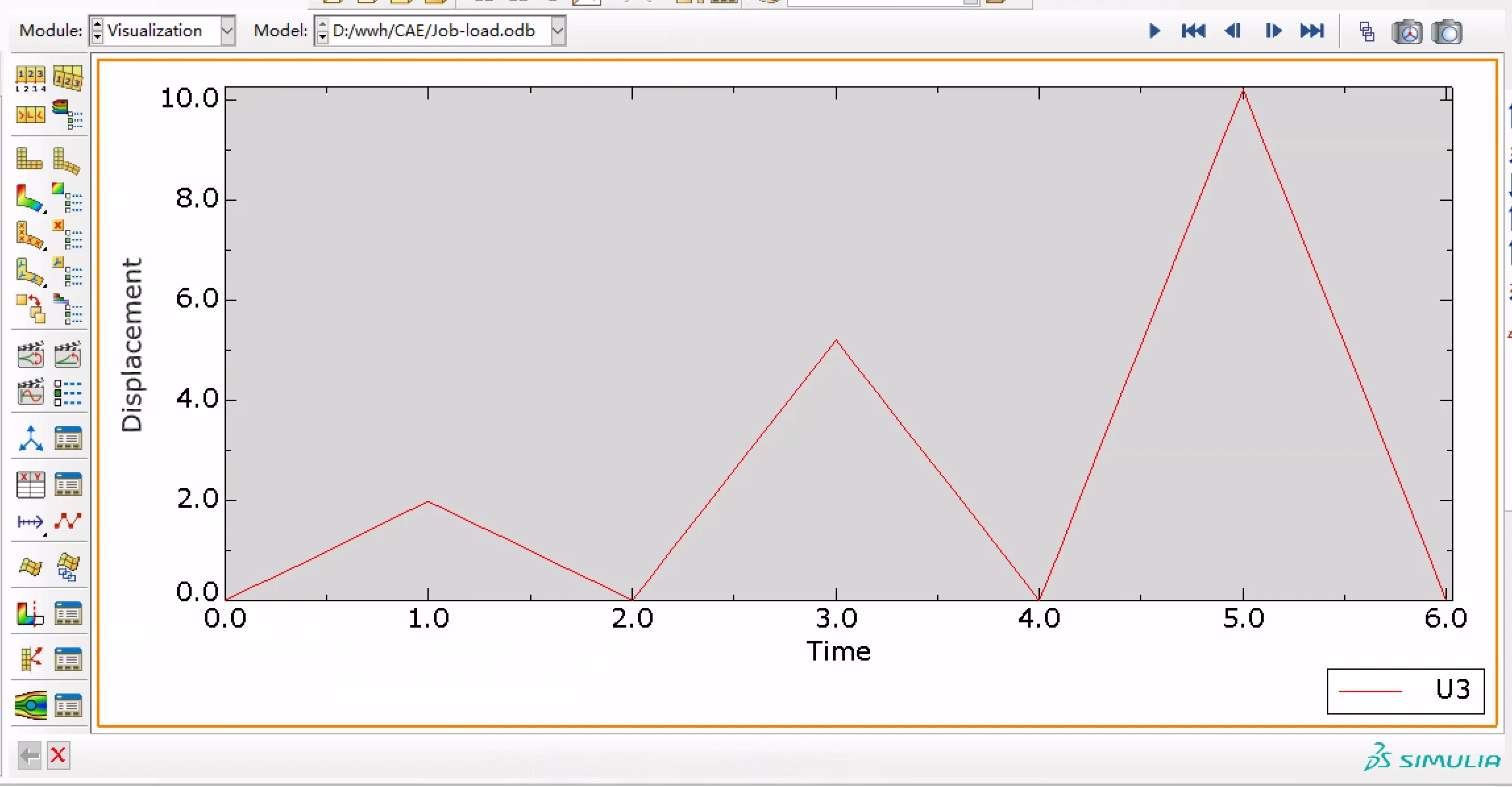
位移随时间的变化
然后操纵XY数据得到加卸载应力应变响应结果(Mullinus效应模拟响应):
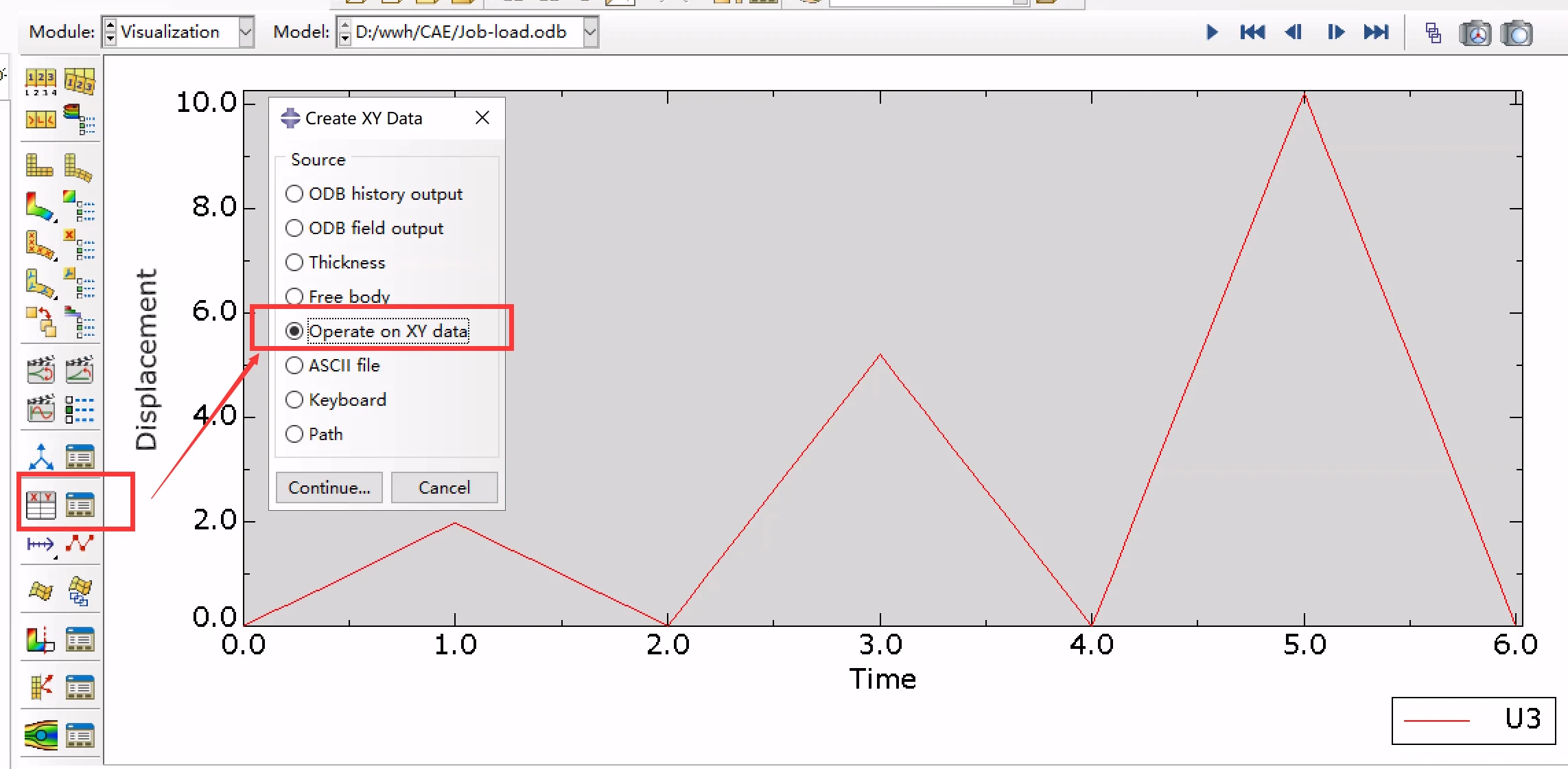
数据处理
使用Combine命令:

数据表达式
绘制表达式:
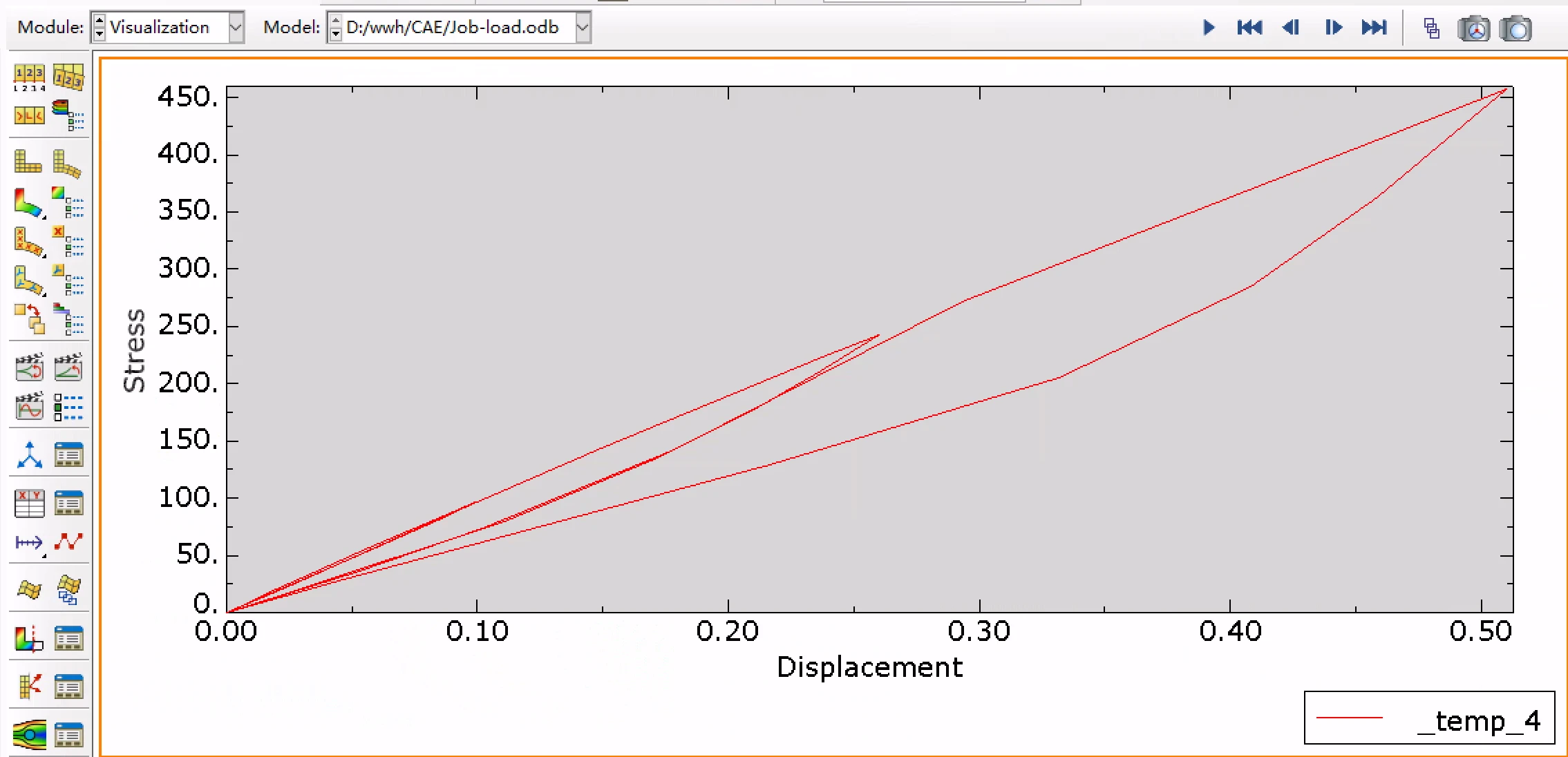
abanqus对mullinus效应的数据拟合响应
导出数据与实验数据进行对比:
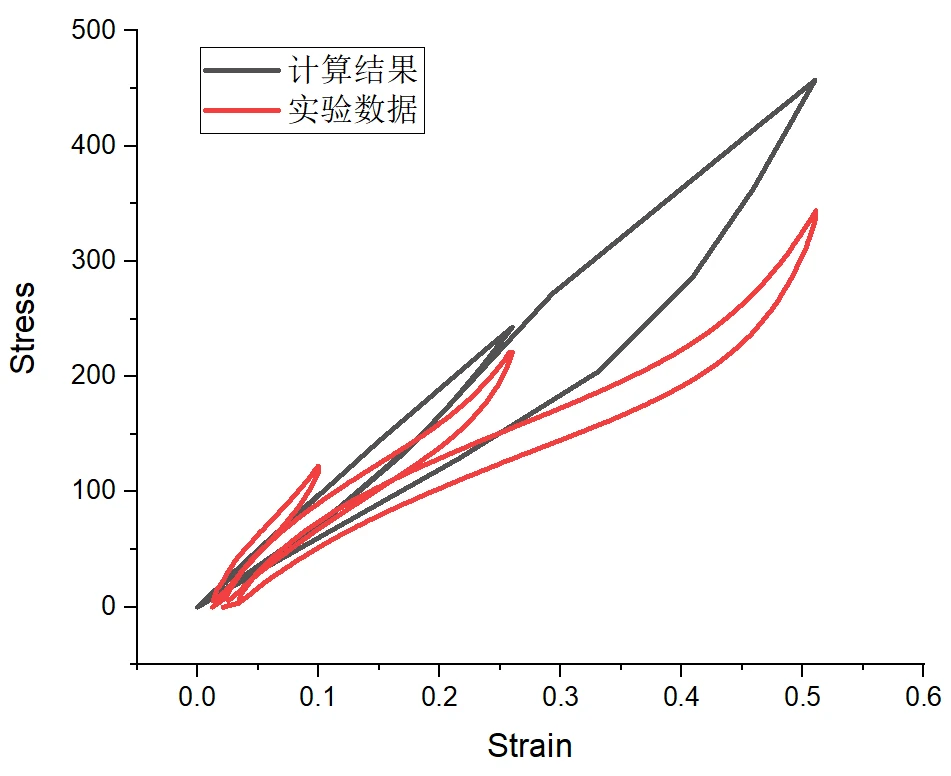
计算结果与实验结果比较
从上图可知,Mullinus效应被abaqus捕获,但拟合效果并不好。

不同泊松比数值计算拟合结果
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删