详解Abaqus材料属性的超弹性定义

在超弹性这一小节包含：类橡胶材料的超弹性、弹性泡沫的超弹性、各向异性超弹性；

#类橡胶材料的超弹性

超弹性材料模型：

是各向同性和非线性的;

适用于对大应变表现出瞬时弹性响应的材料(如橡胶、固体推进剂或其他弹性体材料)；

要求在分析步骤中考虑几何非线性，因为它是用于有限应变应用。

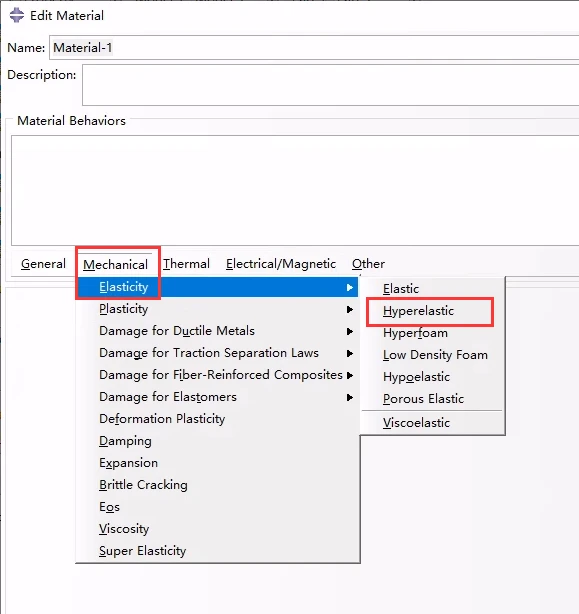
   超弹性定义
 

1. 可压缩性：

大多数弹性体(固体，类橡胶材料)与它们的剪切柔性相比，具有非常小的可压缩性。对于三维固体、平面应变和轴对称分析单元，数值解对可压缩性程度非常敏感。在材料高度受限的情况下(例如用作密封的o形环)，必须正确建模压缩率以获得准确的结果。在材料不受高度限制的应用中，可压缩性的程度通常不是至关重要的;例如，可以在Abaqus/Standard中假设材料是完全不可压缩，即除了热膨胀外材料的体积不会改变。

可以通过泊松比 衡量 材料的可压缩性：

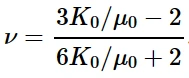
   泊松比为初始体积模量E0和初始剪切模量μ0的函数
 

在Abaqus/Standard中，建议对初始泊松比大于0.495的几乎不可压缩超弹性材料使用固体连续介质混杂单元。除了平面应力和单轴情况外，在Abaqus/Explicit中不可能假设材料是完全不可压缩的，必须提供一些可压缩性。如果在超弹性模型中没有给出材料压缩性的值，默认情况下Abaqus/Explicit假定K0/μ0= 20，即泊松比0.475，这个默认值提供了比大多数弹性体更大的可压缩性。然而，如果弹性体是相对无约束的，这种材料体积行为的软建模通常提供相当准确的结果。不幸的是，在材料高度受限的情况下，例如当它与坚硬的金属部件接触并且具有非常小的自由表面时，特别是当载荷高度压缩时，使用Abaqus/Explicit可能无法获得准确的结果。

2. 各向同性假设：

在Abaqus中，所有的超弹性模型都是基于在整个变形历史中各向同性行为的假设。因此，应变势能可以表示为应变不变量的函数。

3. 应变势能：

超弹性模型的定义需要选择应变势能的计算方法：

   应变势能的选择
 

超弹性材料用“应变能势”U (ε)来描述，U (ε)定义了每单位参考体积(初始构型中的体积)中存储在材料中的应变能作为材料中该点应变的函数。在Abaqus中有几种形式的应变能势可用来模拟近似不可压缩各向同性弹性体:the Arruda-Boyce form, the Marlow form, the Mooney-Rivlin form, the neo-Hookean form, the Ogden form, the polynomial form, the reduced polynomial form, the Yeoh form, and the Van der Waals form.

通常，当有多个实验试验数据时(通常至少需要单轴和等双轴试验数据)，Ogden 和Van der Waals形式在拟合实验结果时更为准确。如果可用于校准的测试数据有限，则Arruda-Boyce, Van der Waals, Yeoh或reduced polynomial forms形式提供合理的行为。当只有一组测试数据(单轴、等双轴或平面测试数据)可用时，建议使用Marlow，它将准确地再现测试数据，并在其他变形模式下具有合理的行为。

Abaqus/CAE允许通过使用选定的应变能势自动创建响应曲线来评估超弹性材料的行为。此外，还可以在不指定特定应变能势的情况下提供材料的实验测试数据，并使用Abaqus/CAE对材料进行评估，以确定最佳应变能势。

   导入实验数据
 

注意名义应力应变为工程应力应变，非真实应力应变：

   数据为名义应力应变
 

下面是一组实验测得的柔性弹性体的单轴拉伸实验数据（工程/名义应力应变）：

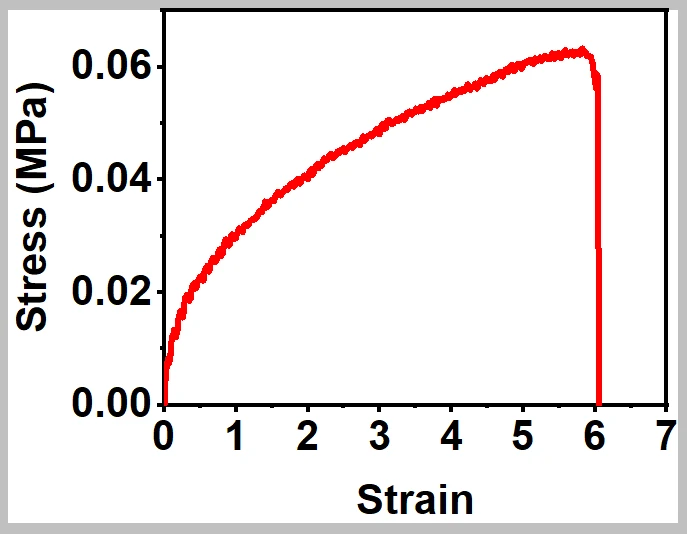
   实验数据
 

先将其数据预处理：使得数据为递增的形式，可以使用origin等软件进行多项式拟合曲线：

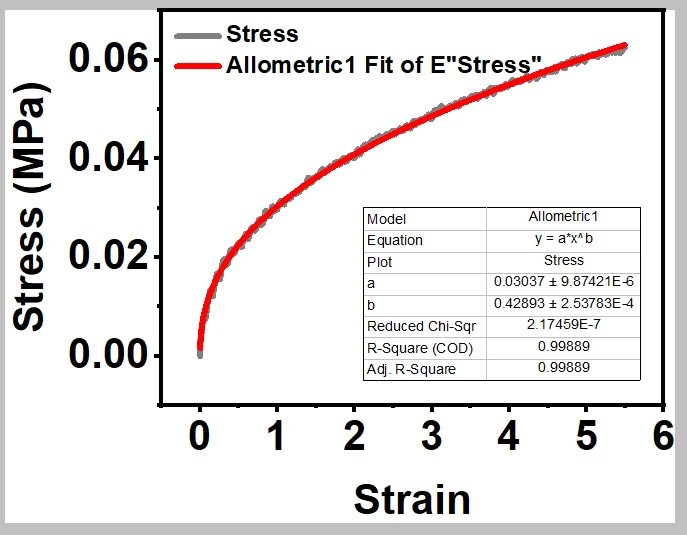
   拟合后，数据为递增形式
 

将其导入/复制到单轴拉伸试验数据表中：

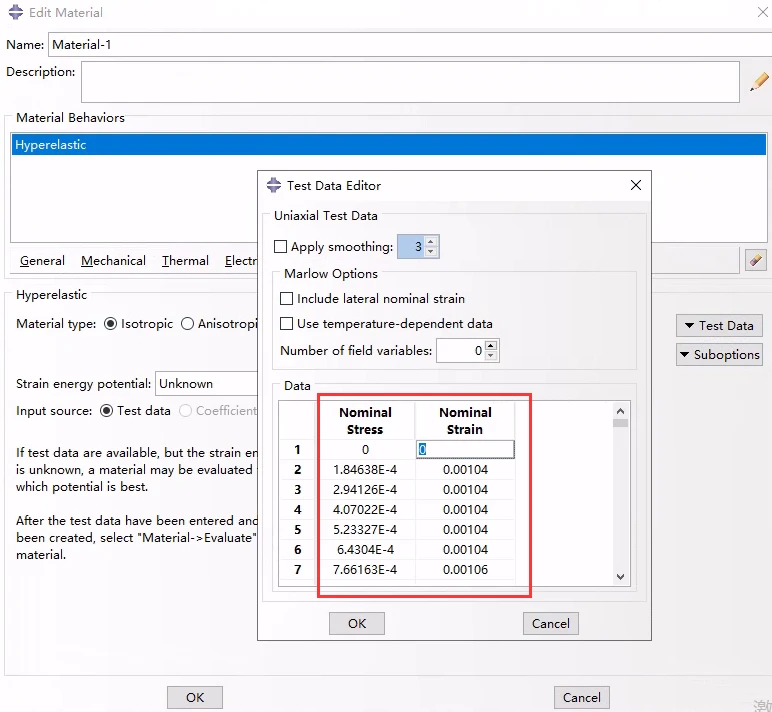
   将实验数据复制到表中，初始为0
 

确认选项，然后点击OK。

   超弹性实验数据材料评估
 

然后对刚刚创建的材料进行评估，以确定哪一种应变势能拟合更好，并得到应变势能的各参数：

   材料评估
 

进一步在“Test setup”中确认材料数据源即是否单轴拉伸，在下面栏中勾选拟合的结果曲线，并可修改应变范围：

   例如此处仅拟合单轴结果，应变范围修改为0-6
 

在应变势能选项卡中，便可选择想要拟合的应变势能形式，勾选后确认：

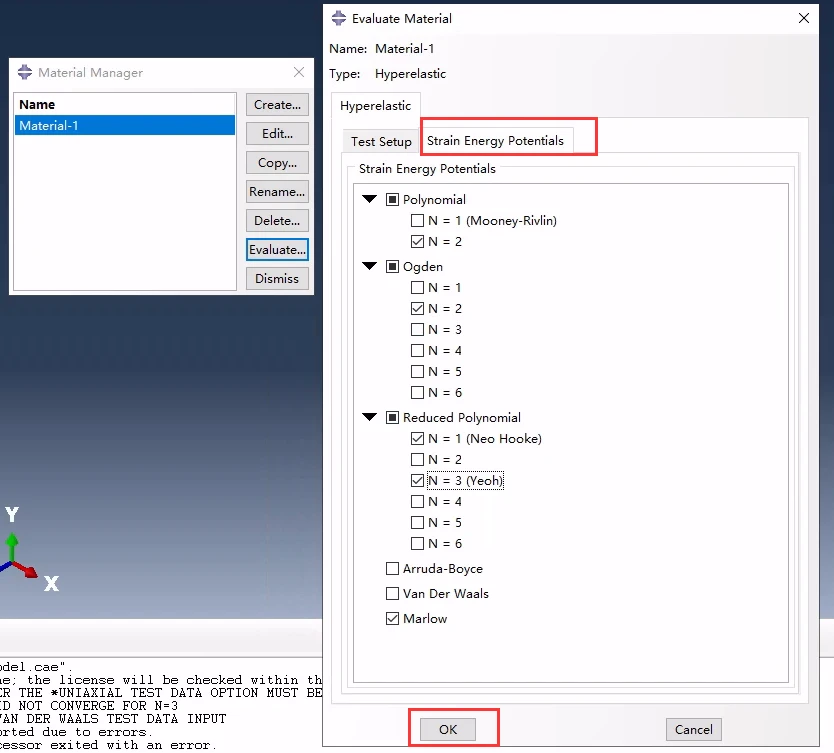
   应变势能
 

Abaqus将自动计算系数并拟合：

   拟合结果
 

并给出每一种拟合的参数：

   拟合参数
 

最后选择较好的拟合类型，并记下他的拟合参数，返回到材料属性定义中，将该材料属性选择对应的应变势能类型，然后采用直接给定系数的方式输入设置即可。

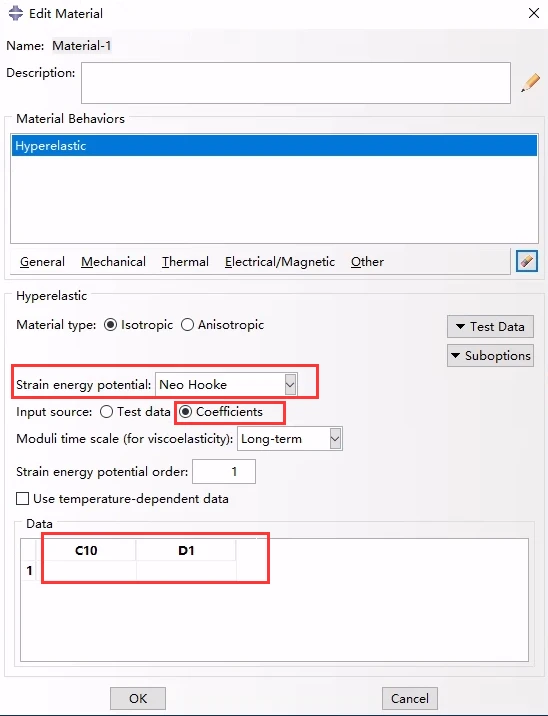
   直接给定应变势能计算系数
 

4. 粘弹性和滞回材料的超弹性：

粘弹性材料(时域粘弹性和平行流变框架)和滞回材料(弹性体中的滞回)的弹性响应可以通过定义这类材料的瞬时响应或长期响应来指定。为了定义瞬时响应，必须在比这些材料的特征弛豫时间短得多的时间范围内进行实验。如果使用长期弹性响应，则必须在比这些材料的特征松弛时间长得多的时间跨度之后收集实验数据。长期弹性响应是弹性材料的默认行为。

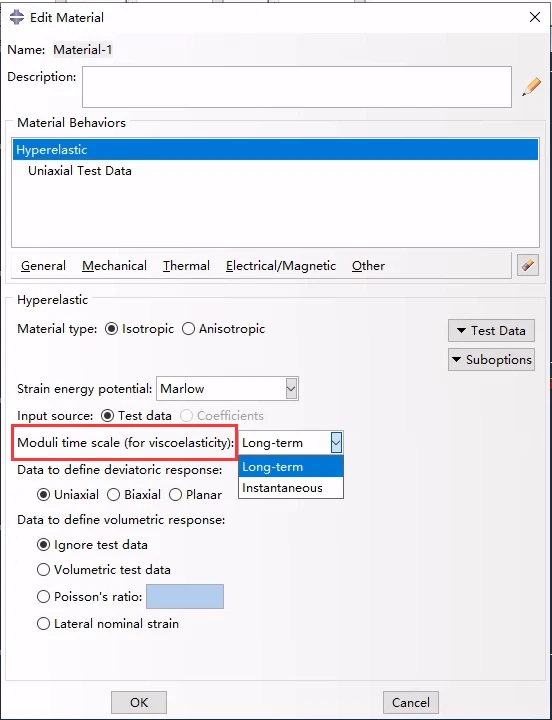
   粘弹性材料的时间尺度
 

5. 实验测试：

   实验测试
 

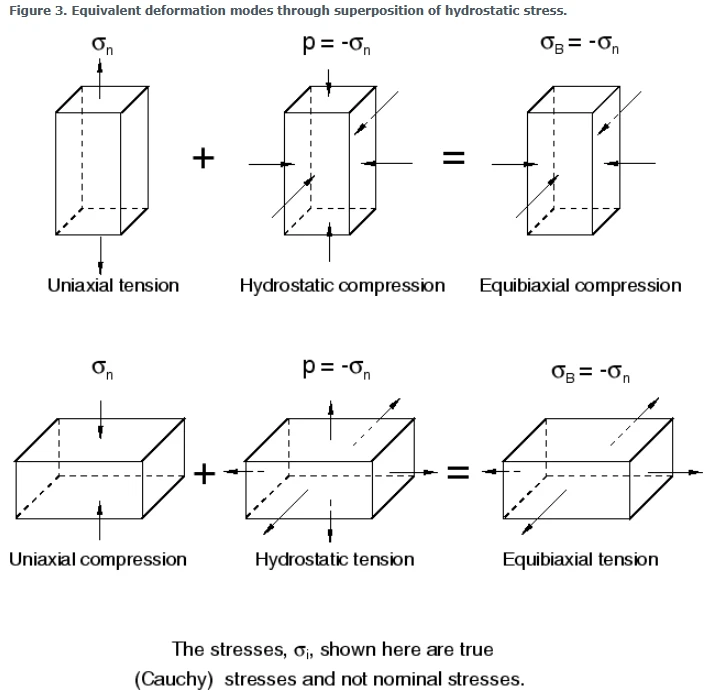
   等效实验
 

6. 单元适用性：

超弹性材料模型可用于实体(连续体)单元、有限应变壳(S4除外)、连续体壳、膜和一维单元(桁架和钢筋)。在Abaqus/Standard中，超弹性材料模型也可以用于Timoshenko梁(B21, B22, B31, B31OS, B32, B32OS, PIPE21, PIPE22, PIPE31, PIPE32，以及它们的“混合”等效物)。它不能与欧拉-伯努利梁(B23、B23H、B33和B33H)和小应变壳(STRI3、STRI65、S4R5、S8R、S8R5、S9R5)一起使用。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删