Abaqus中的自适应网格划分技术结合了纯拉格朗日分析和纯欧拉分析的特点。这种类型的自适应网格通常被称为任意拉格朗日-欧拉(ALE)分析。Abaqus文档通常将“ALE自适应网格划分ALE adaptive meshing”简称为“自适应网格划分adaptive meshing”。【ALE: Arbitrary Lagrangian-Eulerian 】
ALE自适应网格是一种工具,通过允许网格独立于材料移动,即使在发生大变形或材料丢失时,也可以在整个分析过程中保持高质量的网格。ALE自适应网格划分不改变网格的拓扑结构(单元元素和连通性),这意味着该方法在极端变形情况下保持高质量网格的能力有一定的局限性。
ALE自适应网格划分不同于Abaqus/Explicit中的纯欧拉分析。纯欧拉支持单个单元内具有多种材料和空隙,从而可以有效地处理涉及极端变形(如流体流动)的分析。相比之下,ALE单元总是100%充满单一材料;将模型中材料的变形限制为单元的变形,但它允许更精确地定义材料边界和更复杂的接触相互作用。
尽管自适应网格技术和用户界面在Abaqus/Explicit和Abaqus/Standard中是相似的,但用例和功能级别是不同的。Abaqus/Explicit中的自适应网格划分旨在模拟大变形问题。它不试图最小化小变形分析中的离散误差。Abaqus/Standard中的自适应网格划分旨在用于声学领域,并用于模拟材料烧蚀或磨损的影响。
1. ALE自适应网格划分的特点
自适应网格划分:
通过允许网格独立于材料移动,可以在严重的材料变形下保持高质量的网格;
在整个分析过程中保持拓扑相似的网格(即,不创建或删除单元)。
Abaqus/ExplicitALE自适应网格:
可以用来分析拉格朗日问题和欧拉问题;
可作为连续自适应网格划分工具,用于大变形的瞬态分析问题(如动态冲击、穿透和锻造问题);
可以用作模拟稳态过程(如挤压或轧制)的求解技术;
可用作分析稳态过程中的暂态相的工具;
可用于显式动力学(包括绝热分析)和完全耦合的热应力过程。
Abaqus/StandardALE自适应网格:
可以用来解决拉格朗日问题和模拟烧蚀或磨损(材料在边界处被侵蚀)的影响;
当结构预压引起声域显著的几何变化时,可用于更新声网格;
可用于几何非线性静态,稳态输运,耦合孔隙流体流动和应力,以及耦合温度-位移分析。
2. 如何设置ALE自适应网格
自适应网格划分可以应用于整个模型或模型的单个部分。拉格朗日自适应网格域将被创建,该域作为一个整体跟随最初在其内部的材料。提供了控制网格的附加选项。在Abaqus/Explicit分析中可以定义欧拉边界,以允许材料流入或流出建模域。
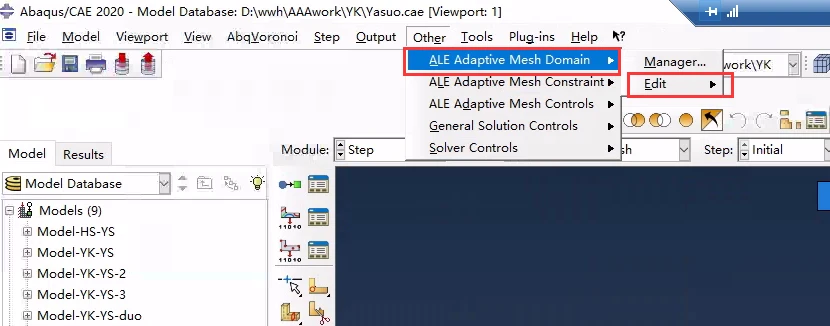
定义的位置
为了充分利用Abaqus中的所有自适应网格特征,理解自适应网格域、边界区域、边界边缘、几何特征和网格约束的概念是很重要的。
具体的操作介绍将分为以下几个内容,将分别在后面几节Abaqus自适应技术(2.n)单独介绍。

ALE自适应网格划分
3. ALE 自适应网格的使用
用于Abaqus/Explicit:
在预计会有大变形的问题中,自适应网格划分所带来的网格质量的提高可以防止由于严重的网格畸变而导致分析终止。在这些情况下,可以使用自适应网格来获得比纯拉格朗日分析更快、更准确、更健壮的解决方案。
自适应网格对于模拟金属成形过程(如锻造、挤压和轧制)特别有效,因为这些类型的问题通常涉及大量不可恢复的变形。由于产品的最终形状可能与原始形状大不相同,因此在加工的后期阶段,当大的材料变形导致严重的单元扭曲和纠缠时,对于原始产品几何形状最优的网格可能变得不合适。在应变浓度高的地区,单元长径比也会降低。这两种因素都可能导致准确性的丧失,稳定时间增量的减小,甚至问题的终止。
用于Abaqus/Explicit:
可以使用自适应网格来使声学域网格遵循边界结构的大变形。在其他应用中,可以使用自适应网格划分和自适应网格约束来模拟任意大量远离域的材料消融。
可以使用自适应网格来使声学域网格遵循边界结构的大变形。在其他应用程序中,您可以使用自适应网格划分和自适应网格约束来模拟任意大量远离域的材料消融。默认情况下,结构声学计算基于声学域的原始配置。只要流体和结构之间的边界在施加预紧力期间没有经历大的变形,这种近似是适当的。然而,当声学域的几何形状由于结构载荷而发生显著变化时,必须更新原始声学配置。一个例子是轮胎的内腔受到充气,轮辋安装,和足迹压力载荷。
Abaqus中的声学单元不具有力学行为,因此不能模拟结构发生大变形时流体的变形。Abaqus/Standard通过周期性地创建一个新的声学网格来解决声学域当前结构的计算问题,该声学网格使用与原始网格相同的拓扑结构,但调整了节点位置,使结构-声学边界的变形不会导致声学单元的严重畸变。
在随后的结构声耦合分析中,考虑到与新声网格相关的几何变化。然而,假设流体的材料特性,如密度,不会因为网格平滑而改变。
自适应网格划分还可以通过定义独立于底层材料运动的边界网格运动来模拟烧蚀或磨损的效果。一个例子是轮胎在其使用寿命期间的磨损,这种影响会显著影响结构的性能。
4. Abaqus/Explicit和Abaqus/Standard中ALE自适应网格划分的比较
与Abaqus/Standard中的自适应网格划分相比,Abaqus/Explicit中的自适应网格划分通常更健全,并且提供了更多控制网格的功能。
Abaqus/ExplicitALE自适应网格:
Abaqus/Explicit中的自适应网格划分旨在处理各种各样的问题,采用各种平滑方法,可以使用控件来定制针对特定问题的适应性:
创建完全欧拉模型;在变形开始之前首先提高网格的质量;定义示踪粒子,使跟踪和输出基于材料的结果数量。
Abaqus/StandardALE自适应网格:
Abaqus/Standard中的自适应网格划分使用单一平滑算法,可以很好地用于结构声学分析和烧蚀过程建模。Abaqus/Standard自适应网格划分有以下限制:
初始网格扫描不能用于提高初始网格定义的质量;该方法不能用于一般的大变形问题,如块体成形;诊断能力目前有限。
5. 自适应网格应用的简单示例
为了说明自适应网格划分的价值,给出瞬态和稳态成形应用的简单例子。为简单起见,均使用二维建模,且都使用Abaqus/Explicit。
例1:轴对称的锻件
在这个例子中,一个润滑良好的正弦形状的刚性模具向下移动,使矩形截面的毛坯变形
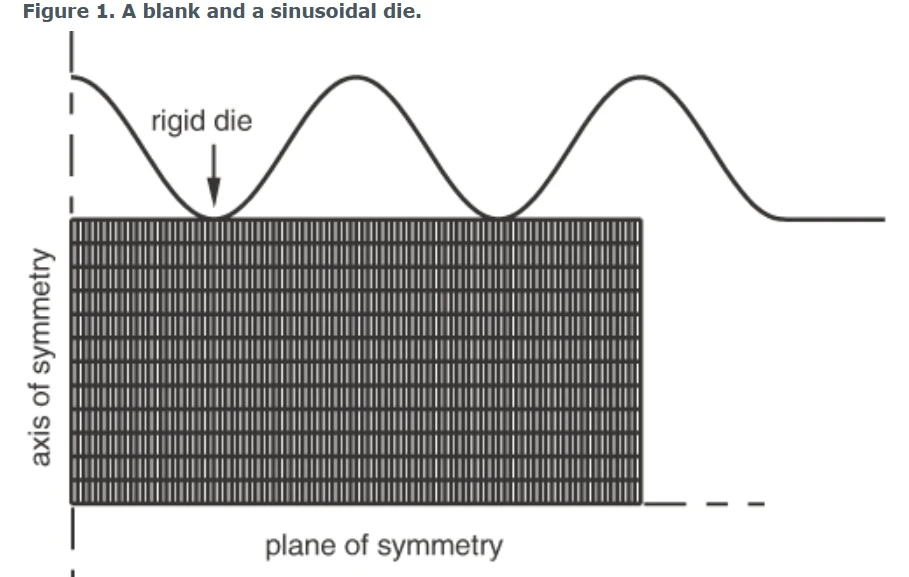
压痕深度为原毛坯厚度的80%。当坯料缩进时,材料向上和向外(径向)挤压。模具采用解析刚体曲面建模,坯料采用规则网格结构的轴对称连续单元建模。假定坯料具有弹塑性材料特性。
当采用纯拉格朗日分析时,计算无法完成,因为在几个单元中存在过度的扭曲:

纯拉格朗日分析因单元畸变过大而终止
自适应网格划分允许问题运行到完成。为整个毛坯创建拉格朗日自适应网格域。Abaqus/Explicit自动为自适应网格选择合适的默认值:
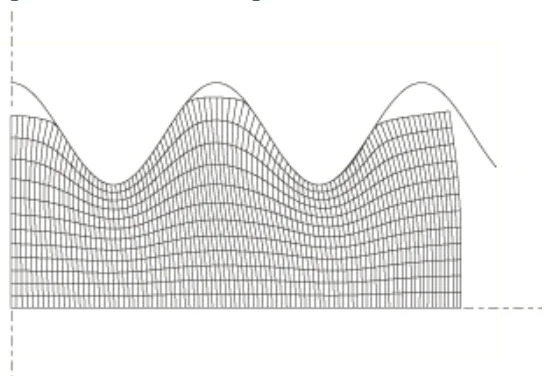
在ALE分析的中间阶段变形的构型
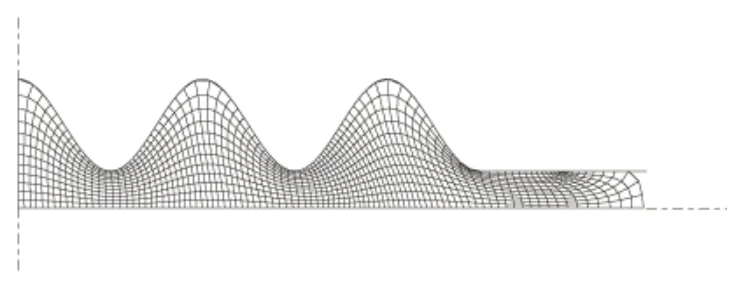
ALE分析完成后变形的构型
例2:稳态滚动
这个例子展示了在稳态模拟中使用自适应网格,以允许材料在问题域上的欧拉边界流动。钢板通过轴对称辊架,使其高度降低50%。模拟一直运行到达到稳态状态。
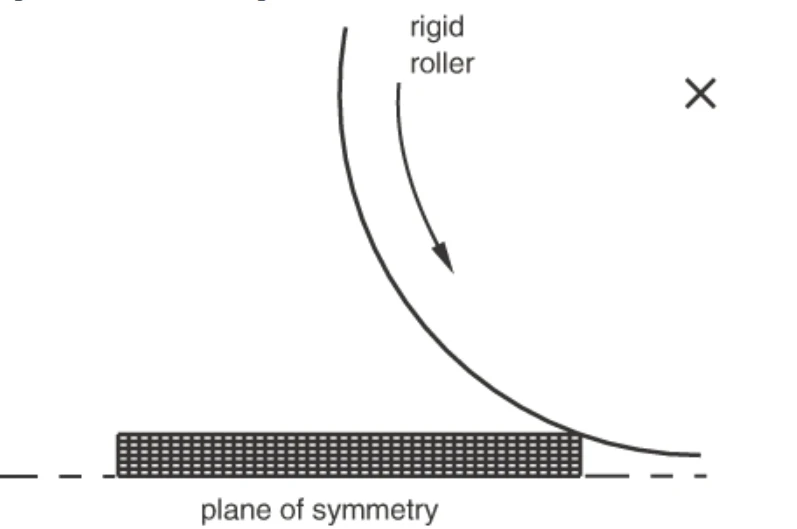
纯拉格朗日模型中辊筒和未变形坯料的初始形态
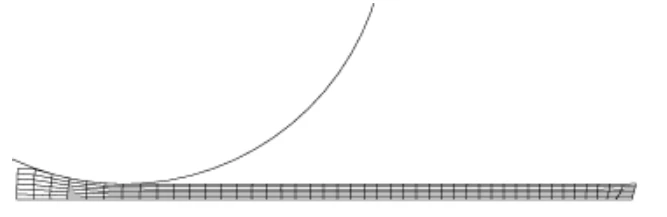
纯拉格朗日模型的最终稳态构型
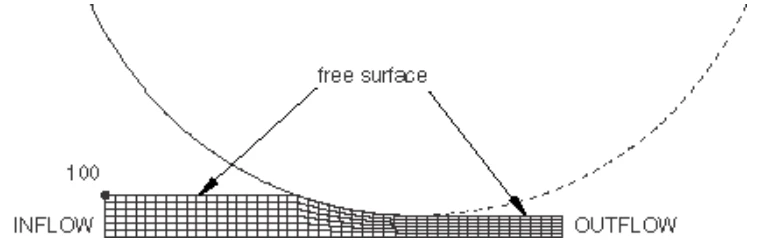
初始欧拉自适应网格域
仅对滚子附近的区域进行建模。不需要知道自由表面的确切位置:它在一个可能的位置创建,最终的稳态位置作为求解的一部分被找到。虽然没有显示,一个聚焦网格可以用来捕捉陡峭的应变梯度。欧拉域得到与拉格朗日方法相同的稳态解。
欧拉自适应网格域是通过在自适应网格域上定义流入边界和流出边界来创建的。自适应网格约束法线应用于这些边界,这样材料就会流过网格。辊筒与坯料之间的摩擦接触通过自适应网格域拉动材料。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删