Abaqus自适应技术概览

“ adaptivity 适应性 ”反映了Abaqus调整网格以满足分析目标的自适应或求解依赖的过程。

1. 选择一种自适应技术

Abaqus中有三种自适应技术:

Arbitrary Lagrangian-Eulerian (ALE) adaptive meshing：任意拉格朗日-欧拉自适应网格划分;

varying topology adaptive remeshing：变拓扑自适应网格重划分；

mesh-to-mesh solution mapping：网格到网格的求解映射；

   对比
 

1.1 ALE adaptive meshing

任意拉格朗日-欧拉(ALE)自适应网格划分提供了网格畸变控制。ALE自适应网格划分使用单个网格定义，在分析步中逐渐平滑。ALE自适应网格在Abaqus/Standard中应用有限，在Abaqus/Explicit中更普遍适用。纯粹的拉格朗日分析，其中节点运动对应于物质运动；纯粹的欧拉分析，其中节点在空间中保持固定，物质通过单元“流动”；ALE分析通常使用介于这两个极端之间的方法。在发生大变形或材料丢失的情况下，自适应网格可以控制单元变形。图1说明了自适应网格限制网格变形的一个案例。

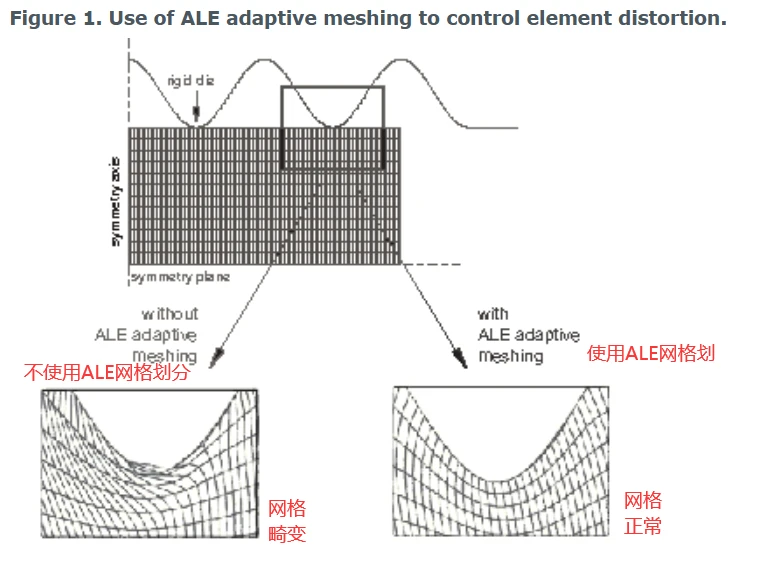
   图1 采用ALE自适应网格划分控制单元畸变
 

与其他自适应技术不同，自适应网格划分操作针对原始网格定义，因此，只有当单个网格在模拟期间有效时才有用。通过平滑网格节点来适应网格。这种平滑通常在分析步骤中频繁应用。ALE自适应网格划分只需要一个分析job。

1.2 Adaptive remeshing (varying topology adaptivity)

自适应网格划分通常用于精确控制，尽管在某些情况下它也可以用于失真控制。自适应重划分过程涉及多个不同网格的迭代生成，以确定在整个分析中使用的单个优化网格。自适应重网格只适用于从Abaqus/CAE提交的Abaqus/Standard分析。自适应重划分的目标是获得满足网格离散误差指标的求解方案，同时最小化单元数量，从而减少分析成本。可以使用自适应重划分来获得求解方案成本和所需精度之间的平衡。图2说明了利用自适应重划分将圆角周围网格细化提高了应力结果质量的例子。

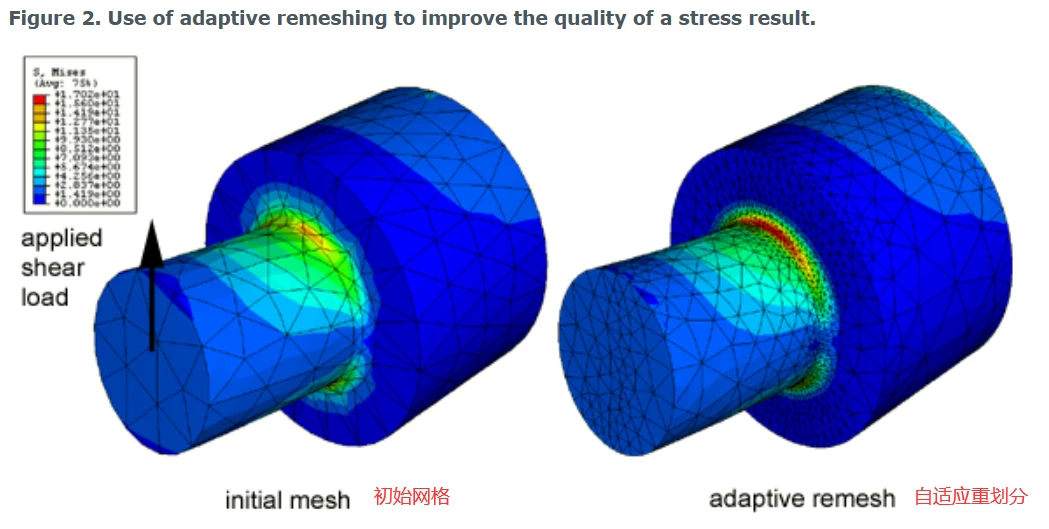
   图2 使用自适应重划分提高应力结果的质量
 

自适应重划分涉及一个迭代过程，以确定用于分析的单一优化的网格。在Abaqus/CAE中控制迭代过程和网格重划分。需要多个分析作业求解，每个分析作业的仿真历史是相同的。一个过程多个计算作业比较。

1.3 Mesh-to-mesh solution mapping

网格到网格的求解映射仅在Abaqus/Standard中可用。可以使用这种技术来控制单元失真，在大变形发生时更换网格并继续分析。图3说明了通过新网格与求解映射的联合使用解决了单元失真的问题。

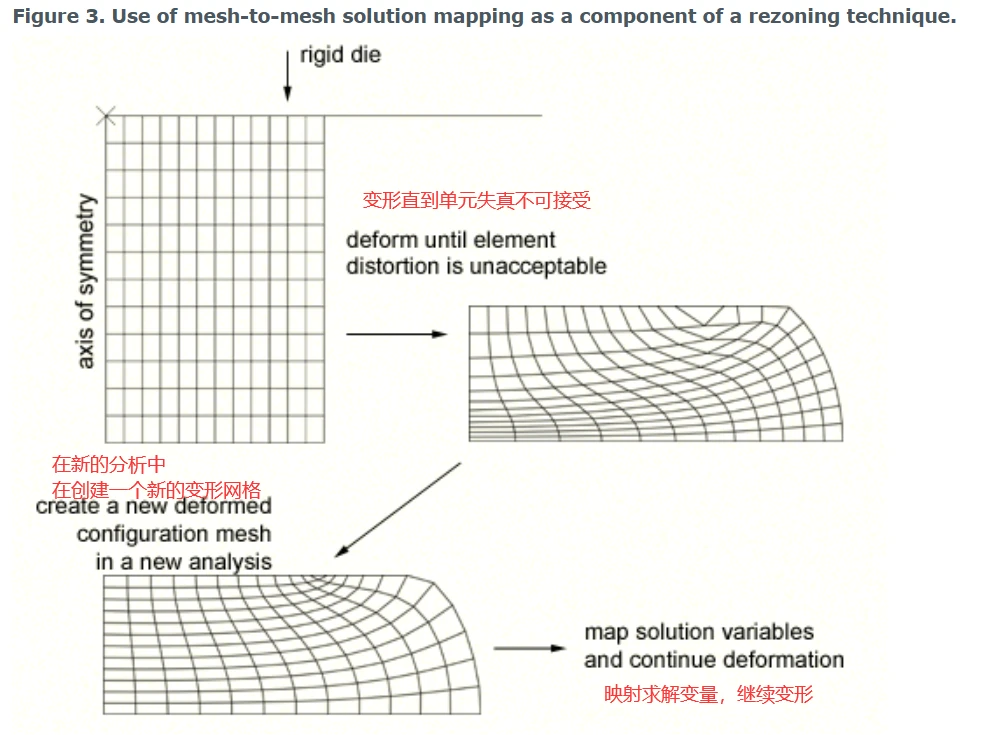
   图3 使用网格到网格的求解映射
   

网格替换或重新划分涉及创建多个Abaqus作业，每个作业都代表模型在不同的、连续的仿真历史时期的过程。一个过程分多个作业连续求解。当单个网格在模拟过程中不能有效时，可以使用网格替换。初始配置之后的每个网格都反映了模型的解相关变形。因此，使用网格替换的分析是顺序依赖的，Abaqus使用网格到网格的求解映射将解变量从一个分析传递到下一个分析。

2. 总结

按自己的理解很好区分：

ALE自适应网格，只有一个分析job一个网络，介于拉格朗日与欧拉分析，控制网格畸变；

自适应网格重划分：多个分析job各一个网络，每个分析job都是完整过程计算，其实本质主要是网格质量的优化。

网格映射方法：多个分析job各一个网络，多个分析job顺序计算，解传递以实现完整过程的分析，感觉像是重启动分析。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删