ABAQUS子模型技术概览

子模型是在全局模型分析结果的基础上研究局部模型的方法。通过初始的全局模型分析计算来确定在激励载荷作用下的最大响应区域，子模型方法不需要细化或重分析整体模型，只需截取局部关注区域模型并细化其网格从而提高分析精度。即采用粗网格模型得到局部关注区域周围的结果，采用局部区域网格细化得到局部分析结果。如下图所示。

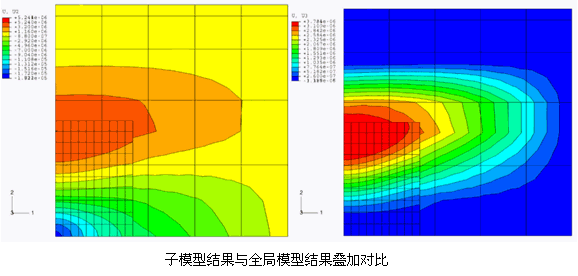
子模型方法是基于Saint-Venant's 定理，要求子模型边界足够远离子模型响应的关注区域。因为建立子模型时没有一个明确的限制来保证结果有意义，因此需要用户自己判断子模型建立的正确性。如何判断子模型建立的正确性，一般的方法是查看子模型边界附近的结果变量值及云图变化与全局模型是否一致，如果结果一致，则认为该子模型是有效的。

Abaqus提供两种子模型技术：基于节点的子模型技术与基于面的子模型技术。基于节点的子模型技术是使用全局模型节点位移结果场插值到子模型边界节点的技术，它能够得到相对更精确的位移结果，适用于任何分析类型；基于面的子模型技术是使用应力场值到子模型边界处的表面积分点上，这种子模型技术能够得到相对更精确的应力结果，但其只能应用于体网格模型和静态分析中。

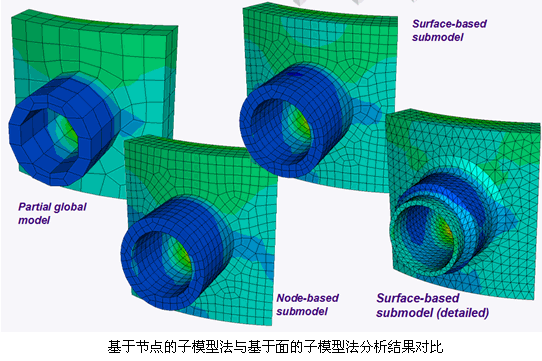
子模型法分析流程：

1、定义问题；

2、运行全局模型，确定驱动子模型的变量输出；

3、检查全局模型结果，特别要注意用于驱动子模型的区域周围不能出现局部不合理现象；

4、定义子模型；

5、根据全局模型的载荷加载子模型的载荷；

6、应用子模型边界条件；

7、需要时定义惯性释放；

8、运行子模型分析；

9、查看子模型结果。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删