基于子模型-全局模型技术的Abaqus微动疲劳分析

1计算任务的描述

交变荷载作用下金属板材及构件的微动疲劳问题是复杂服役状态下土木工程结构及设备所面临的主要挑战和难题。本说明书首次提出了基于子模型和全局模型技术的微动疲劳有限元模拟方法，并利用晶体  塑性有限元方法模拟了pad和轴向体应力作用下specimen的微动疲劳过程，并根据等效塑性应变分布云图识别出模型内部和接触表面最先发生起裂的薄弱部位。我们所提出的方法考虑了试样晶粒尺寸、形态和组构等细观特征，克服了宏-细观尺度耦合问题，可从物理层面分析试样的微动疲劳特征并预测其初始起裂寿命。

本计算任务书主要说明了利用Abaqus软件完成的300次循环加载的微动疲劳模拟结果。

2 仿真计算采用的设备基本情况（CPU、内存等）

计算采用移动工作站Dell Precision 7550，CPU为至强W-10885M四核处理器；内存为128GB。

3 计算模型的处理技术

1）子模型-全局模型耦合技术

2）晶体塑性有限元模拟技术

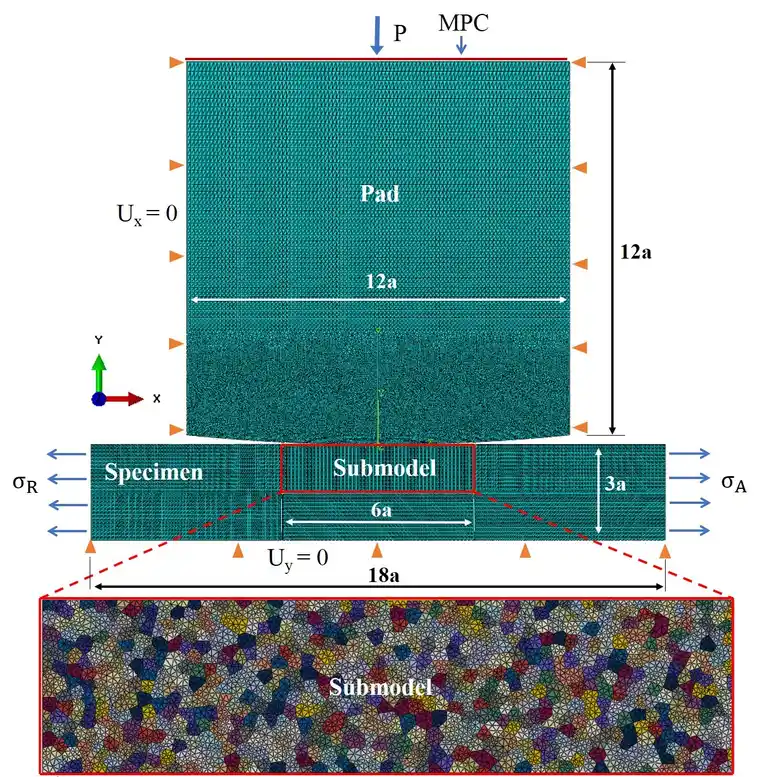
图1 计算模型设计（a为接触半宽）

计算模型采用了子模型-全局模型耦合技术。模型尺寸如图1所示。

子模型微动疲劳模拟技术可归纳为如下步骤：

a)第一步，分别建立粗网格全局模型和局部区域细化的子模型，并沿子模型边界部位切割全局模型；

b)第二步，对宏观全局模型进行微动疲劳分析，并保存子模型边界附近的分析结果；

c)第三步，定义子模型边界，设置各个分析步中的驱动变量(driven variables)，并对细观子模型进行微动疲劳分析

d)第四步，比较全局模型和子模型在子模型边界附近的分析结果，验证子模型设置的有效性。

4 方法计算的机时耗费情况

计算耗费时间约20个小时。

5仿真计算的结果分析

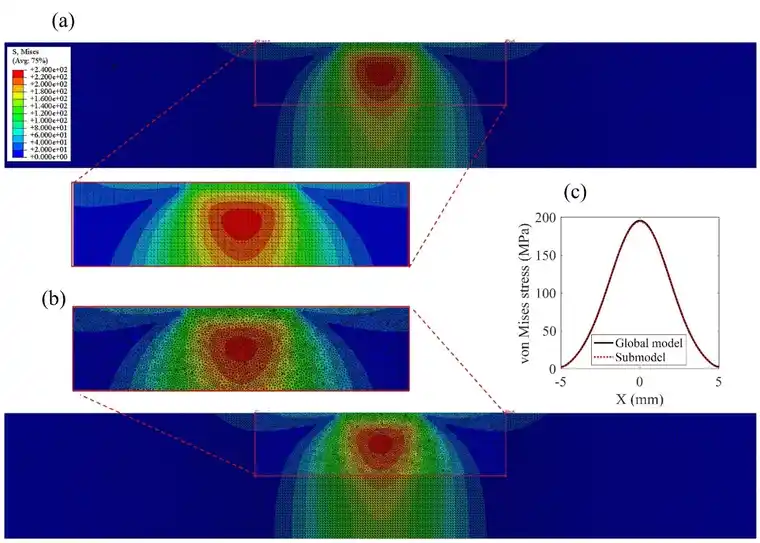
图2 竖向荷载作用下，试验的(a)全局模型, (b)子模型区域范围内的全局模型, (c)子模型Mises应力云图和(d) 底部边界应力曲线。

基于圣维南原理，子模型的边界应充分远离子模型响应的感兴趣区域，以便进行有效的子建模分析，但子模型边界离所关注区域的距离为多少才合适尚无定论。因为建立子模型时没有一个明确的标准来保证结果有意义，因此需要用户自己判断子模型建立的正确性。如何判断子模型建立的正确性，一般的方法是查看子模型边界附近的结果变量值及云图变化与全局模型是否一致，如果结果一致，则认为该子模型是有效的。对于微动疲劳子模型而言，需要查看子模型边界附近的结果变量值及云图变化与全局模型是否一致。当竖向荷载P = 5800 N 施加完成后, 弹性域内全局模型与子模型应力分布如图2所示。图2(b)和2(c)可见，子模型左、右边界处的全局模型应力云图与子模型应力云图量值和分布状态均一致。此外，子模型底部边界处的应力分布曲线与该部位全局模型应力分布曲线重合。由此可见，本文所采用的子模型分析方法是合理有效的。

图3  (a) 应力等值线和 (b) 在第 300 次循环微动载荷下的等效塑性应变分布。

当加载到第300次轴向加载应力(axial bulk stress _σA)最大时(t=30s)，计算模型应力及有效塑性应变分布见图3。如图3(a)和图3(b)所示，我们发现fretting sample内部存在两个塑性应变极大值区域，一个位于pad-specimen 接触界面，另一个位于specimen模型内部。Pad和fretting specimen接触面附近的应力极值区域M和等效塑性应变极值区域M’基本重合，二者均位于接触后缘。在有效塑性应变极值区域M’内接触表面处单元E1714塑性应变值最大，达到4.68×10^-5，其左右两个相邻单元塑性应变值也分别达到4.07×10^-5和3.70×10^-5。在模型内部有效塑性应变最大单元位于接触中线附近、specimen表面以下1.28 mm深度处N点(所在单元为E2608)，其等效塑性应变值达到5.648×10^-4。

6 结论

我们采用的子模型-全局模型耦合技术可以较好地克服模型尺寸限制和存储能力制约，实现宏-细观耦合微动疲劳模拟。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删