材料硬化模型详解

当材料达到弹性阶段之后，应力应变关系是非线性的。

Abaqus在非线性阶段看做不同硬化模型，分别提供了Isotropic（各项同性）、Kinematic（随动强化）、Johnson-Cook（与应变率，温度相关）、Combined

有些材料具有包辛格效应，即强化性质随着塑性变形的增加，屈服极限在一个方向上的提高而在相反方向降低，如果涉及到材料在塑性阶段的反复加卸载，就要使用kinematic hardening。

isotropic hardening的yield surface在空间上各个方向的扩大程度都是相同的，而kinematic hardening 的yield surface在空间上只发生移动而大小不变。

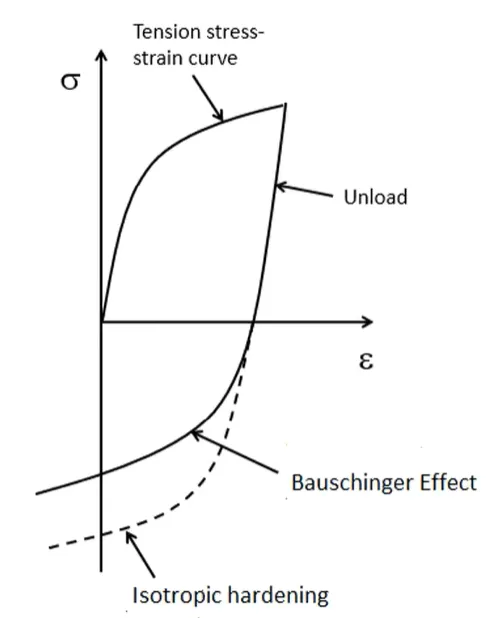
包辛格效应：

在材料塑性加工过程中正向加载引起的塑性应变导致材料在随后的反向加载过程中出现塑性应变软化(屈服极限减少)的现象。这一现象是包辛格于1886年在金属材料的力学性能实验中发现的。当金属材料先拉伸至塑性变形阶段后卸载至零，再反向加载，即进行压缩变形时，材料的受压屈服极限比材料未经拉伸至塑性变形而直接进行压缩的屈服极限明显要小。若先进行压缩使材料发生塑性变形，卸载至零后再拉伸时，材料的屈服极限同样会减少。简单概括为：一个方向的强化会导致另一个方向的弱化。

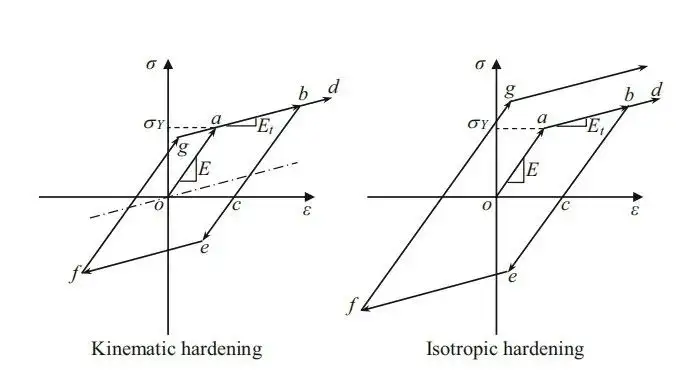
两种应变硬化模型的特点：

随动硬化模型(Kinematic hardening)假设弹性范围（初始屈服应力的两倍）保持不变。弹性范围的中心沿着虚线穿过原点，平行于应变硬化线。因此，线段b–e和f–g长度都相等，并且是o–a长度的两倍。这种特性符合包辛格效应。在各向同性硬化模型(Isotropic hardening)中，假定材料因拉伸后屈服应力增加，而压缩时的屈服应力同样增加，即反向加载的屈服应力大小等于先前屈服应力的大小。也就是说，b点和e点的应力大小相同。因此，在该模型中，弹性范围增大。这种特性不符合包辛格效应。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删