1. 随动硬化模型的使用与校准
线性随动模型近似于具有恒定硬化速率下的硬化行为。该硬化速率应与应用中预期的应变范围相对应的稳定循环中测量的平均硬化速率相匹配。稳定循环是通过在固定的应变范围内循环直到达到稳态条件而得到的;也就是说,直到应力-应变曲线不再从一个周期到下一个周期改变形状。多线性运动硬化模型不受固定硬化速率的限制。更一般的非线性随动模型将给出更好的预测,但需要更详细的校准。
1.1 线性随动硬化模型 Linear kinematic hardening model
从单向拉伸或压缩实验的半循环中获得的测试数据必须线性化,因为这个简单的模型只能预测线性硬化。这些数据通常基于应变循环中稳定行为的测量,覆盖与应用中预期发生的应变范围相对应的应变范围。Abaqus中只需提供两对数据来定义这种线性行为:零塑性应变时的屈服应力σ|0 和 有限塑性应变值εpl时的屈服应力σ。线性随动硬化模量C由关系确定:
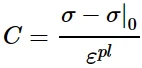
线性运动硬化模量
根据塑性力学概念中的简化塑性模型理论可以很好的理解:

当然也可以提供几组数据对作为温度的函数来定义线性随动硬化模量相对于温度的变化。如果该模型需要Hill屈服面,则必须指定一组屈服比,R i j;
该模型仅适用于相对较小的应变(小于5%)。
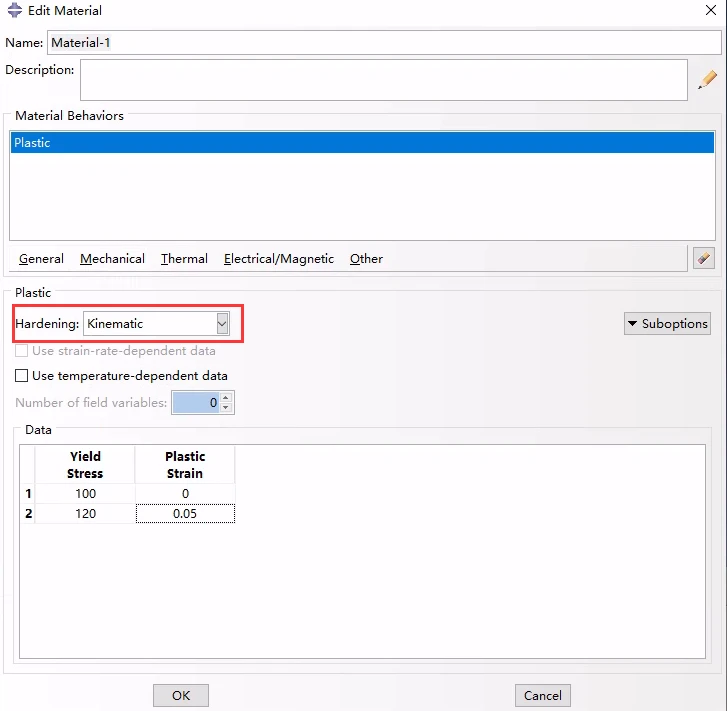
线性随动硬化定义示例
1.2 非线性的各向同性/随动硬化模型
通过定义屈服面的大小作为等效塑性应变的函数表征等效应力的演化,即模型的各向同性硬化分量。可以通过指数定律或直接以表格形式定义各向同性硬化分量;但如果屈服面在整个加载过程中保持固定,则无需定义。在Abaqus/Explicit中,如果模型需要Hill屈服面(各向异性),则必须指定一组屈服比,R i j。在Abaqus/Standard中非线性各向同性/随动硬化模型不能与Hill 屈服面一起使用。
材料参数Ck和γk决定了模型的随动硬化分量。Abaqus提供了三种不同的方法来为模型的随动硬化分量提供数据:直接指定参数C k和γk;可给出半周期试验数据;可给出稳定周期得到的试验数据。校准模型所需的实验如下所述。
★ 用指数定律定义各向同性硬化分量
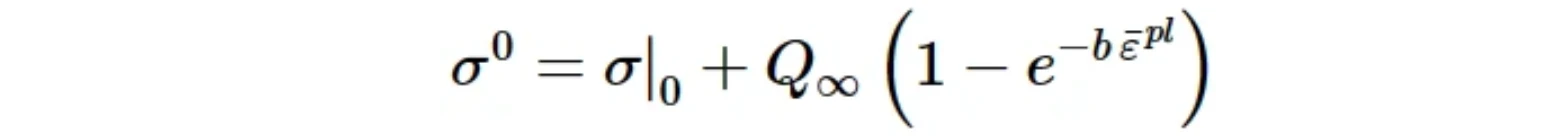
指数硬化
如果已经根据测试数据拟合校准,则直接指定指数律的材料参数σ|0, Q∞, 和 b。这些参数可以指定为温度和/或场变量的函数。
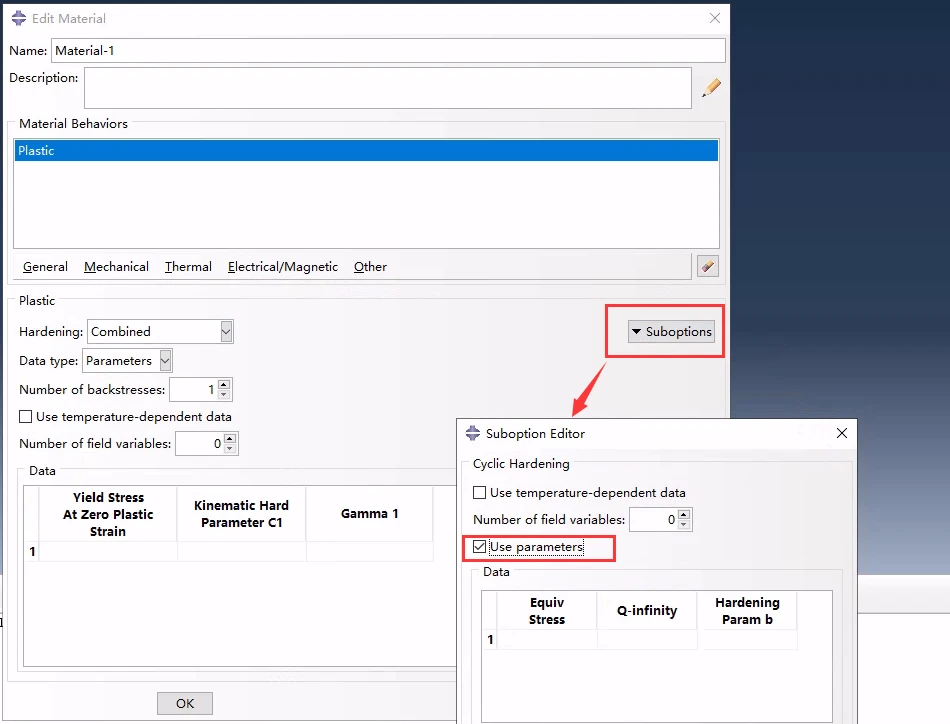
CAE通过指数幂定义各向同性/随动硬化模型的各向同性分量
★ 用表格数据定义各向同性硬化分量
各向同性硬化能够通过指定等效应力即屈服面的大小作为等效塑性应变的表函数定义。获得这些数据最简单的方法是在应变范围Δ ε下进行对称应变控制循环实验。由于材料的弹性模量比其硬化模量大,因此该实验可以近似为在相同的塑性应变范围内的重复循环。
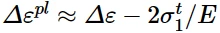
塑性应变的范围 其中E为弹性模量
执行实验:
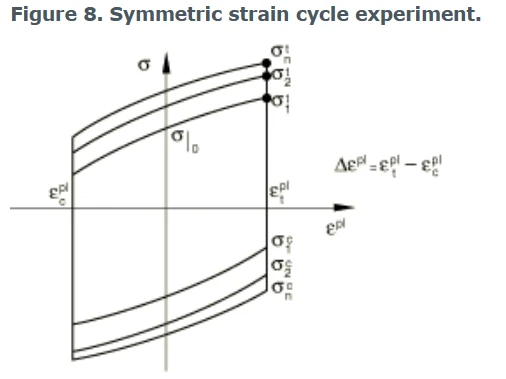
对称应变控制循环实验
决定屈服面大小的等效应力σ|0为等效塑性应变为0时的应力;
模型定义需要指定数据对:
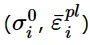
Cyclic hardening定义数据对
,以及零等效塑性应变时σ | 0的值,通过表格形式给出。
其中,等效塑性应变计算为:
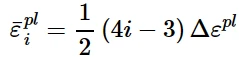
而σ i 0通过将随动分量从屈服应力中分离出来得到:
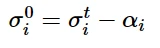
其中:
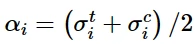
对于每个循环i
由于该模型预测在特定应变水平下每个循环的背应力值大致相同,可近似使用:
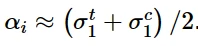
用第一个循环近似
另外,表格数据应提供的是材料可能承受的等效塑性应变范围下的值。数据可以作为温度和/或场变量的函数提供。
为了获得准确的循环硬化数据,校准实验应在分析中预期的应变范围Δ ε下进行。因此,即使一个部件是由相同的材料制成的,它也可能必须被分成几个具有不同硬化性能的区域,对应于不同的预期应变范围,可能通过场变量依赖定义。
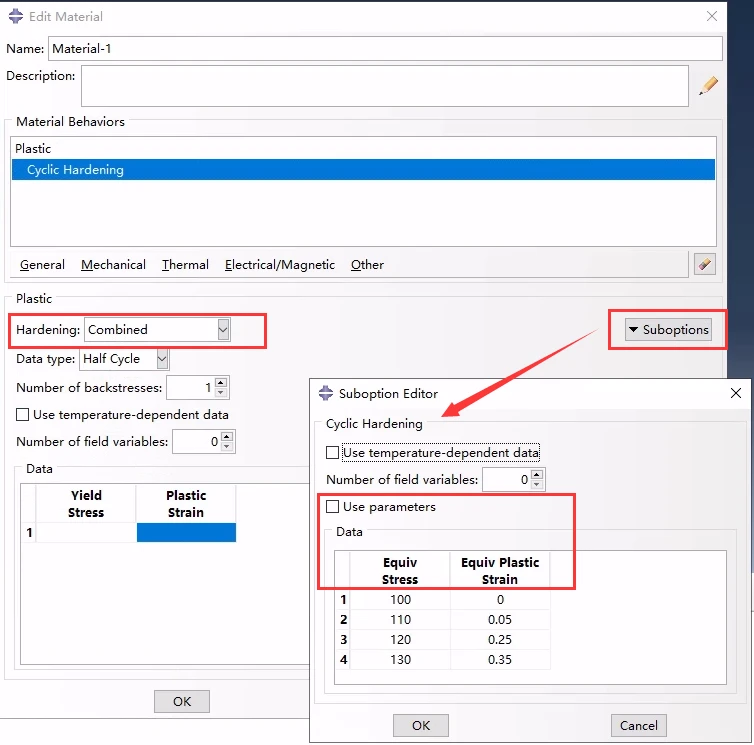
CAE中通过表格数据定义各向同性/随动硬化模型的各向同性分量
★ 在Abaqus/Standard的用户子程序中定义各向同性硬化分量
直接在用户子程序UHARD中指定σ0。σ0可能取决于等效塑性应变和温度。如果用半循环试验数据指定随动硬化分量,则不能使用该方法。
★ 通过直接指定材料参数来定义随动硬化分量
如果已经通过测试数据拟合校准,参数C k和γ k可以直接指定,且可以为温度和/或场变量的函数。当γ k取决于温度和/或场变量时,模型在热力学加载下的响应通常取决于在材料点经历的温度和/或场变量的历史。这种对温度历史的依赖性很小,并且随着塑性变形的增加而逐渐消失。但是,如果不希望这种效果,则应指定γ k为恒定值,以使材料响应完全独立于温度和场变量的历史。目前如果γ k值由于温度和/或场变量而适度增加,用于积分非线性各向同性/随动硬化模型的算法具有精确的解决;然而,如果γ k的值以增量的方式突然变化,则该算法可能无法产生具有足够精度的解。
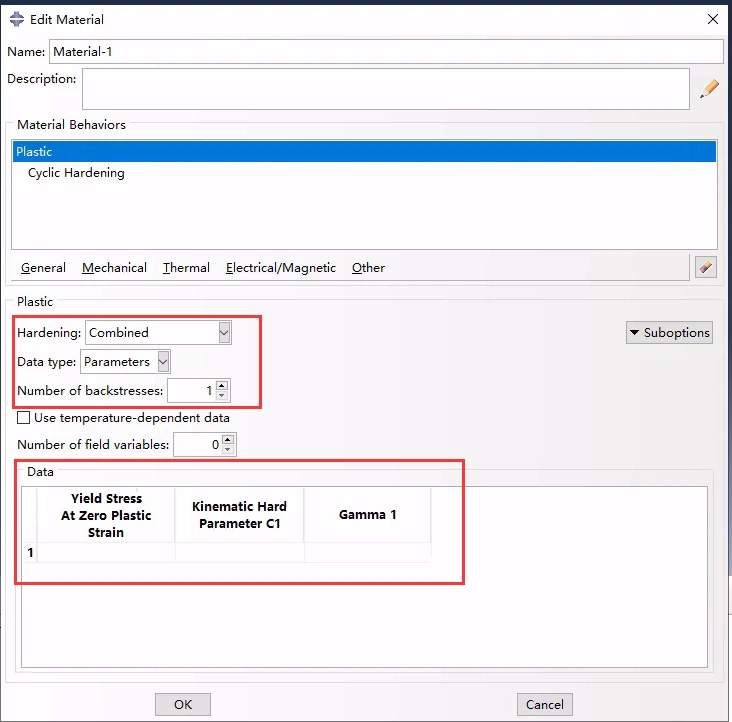
通过直接指定材料参数来定义各向同性/随动硬化模型的随动硬化分量
★ 通过指定半周期循环试验数据来定义随动硬化分量
如果试验数据有限,Ck和γ k可以基于单向拉伸或压缩试验前半周期的应力应变数据。下图显示了此类测试数据的一个示例。当模拟只涉及几个加载周期时,这种方法通常是足够的。

半周期应力应变数据
对于每个数据点(σ i, ε pl i)通过数据表的形式给出,背应力α i值从试验数据中得到(α i为该数据点所有背应力之和)为:
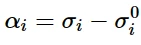
其中σ 0 i为用户定义的各向同性硬化分量(在相应塑性应变下的屈服面大小),如果未定义各向同性硬化分量,则为初始屈服应力。
对半周期内的背应力演化规律进行积分,得到如下表达式:
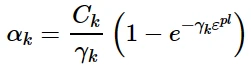
用来校准Ck和γ k
当测试数据作为温度和/或场变量的函数给出时,Abaqus确定几组材料参数(c1, γ 1,…, C N, γ N),每个对应于温度和/或场变量的给定组合。通常,这会导致依赖于温度历史(和/或场变量历史)的材料行为,因为γ k的值随着温度和/或场变量的变化而变化。这种对温度历史的依赖性很小,并且随着塑性变形的增加而逐渐消失。因此,可以使材料的响应完全独立于温度和场变量的历史,通过使用恒定的参数γ k。这可以通过首先运行数据检查分析来实现;在数据检查期间,可以从数据文件中提供的信息确定适当的γ k常数值。参数C k和常数参数γ k的值可以直接输入,如上所述。
当采用多背应力模型时,Abaqus获得不同初始猜测值的硬化参数,并选择与实验数据相关性最好的硬化参数。但是,应该仔细检查获得的参数。在某些情况下,在选择参数集之前获得不同背应力数的硬化参数可能是有利的。
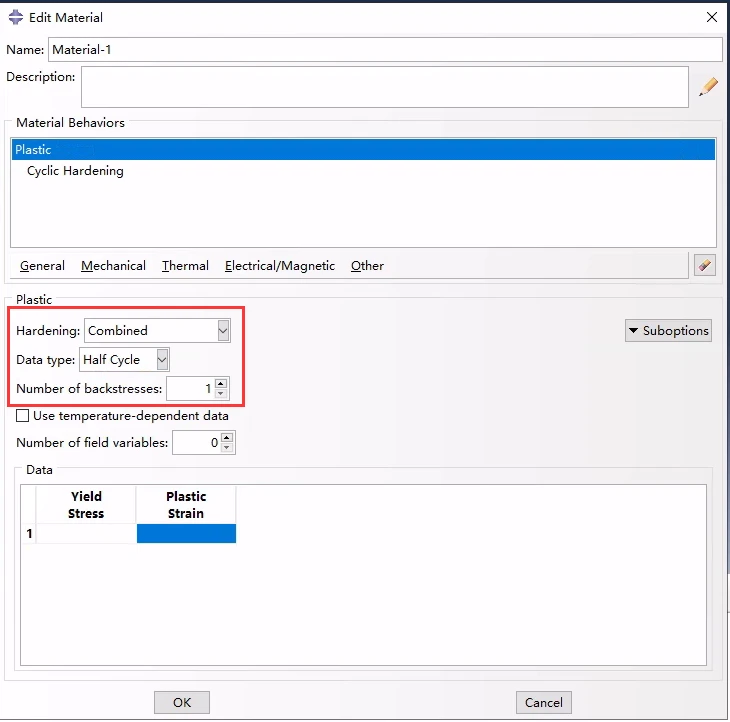
通过指定半周期循环试验数据来定义随动硬化分量
★ 通过指定稳定循环的测试数据来定义运动硬化分量
应力-应变数据可以从受对称应变循环的试样的稳定循环中获得。稳定循环是通过在固定应变范围Δ ε上循环试样,直到达到稳态条件;也就是说,直到应力-应变曲线不再从一个周期到下一个周期改变形状。这样一个稳定的周期如下图所示。
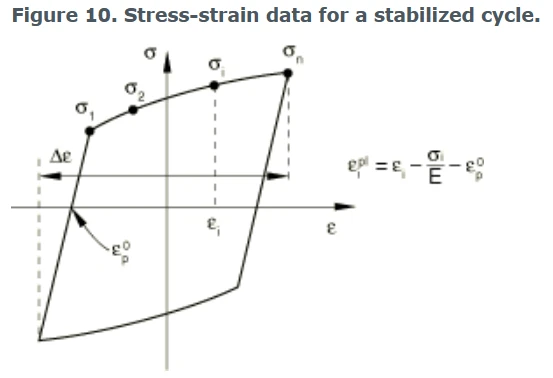
受对称应变循环的试样的稳定循环测试数据
每个数据对(σ i, ε pl i)必须在应变轴移位到ε0p时指定,其中
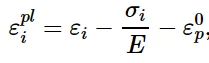
因此有:
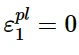
对于每一对(σ i, ε pl i), 背应力α i (α i为该数据点所有背应力之和得到的总背应力)的值为:
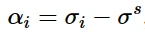
其中,
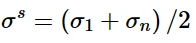
是屈服面的稳定大小
对该单轴应变周期的背应力演化规律进行积分,并与第一个数据对(σ 1,0)精确匹配,得到如下表达式:
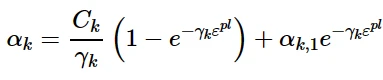
其中,α k, 1表示第一个数据点的k th背应力(k th背应力的初始值)。上述方程可以校准参数Ck和γ k。
如果应力-应变曲线的形状在不同的应变范围内有明显的不同,可能需要得到几个Ck和γ k校准值。在不同应变范围内得到的应力-应变曲线的表格数据可以直接在Abaqus中输入。在数据文件中给出对应于每个应变范围的校准值,以及一组平均参数。Abaqus将在分析中使用平均参数,这些参数可能需要调整,以改善在分析中预期的应变范围内与测试数据的匹配。
当测试数据作为温度和/或场变量的函数给出时,Abaqus确定几组材料参数(c1, γ 1,…, C N, γ N),每个对应于温度和/或场变量的给定组合。通常,这会导致依赖于温度历史(和/或场变量历史)的材料行为,因为γ k的值随着温度和/或场变量的变化而变化。这种对温度历史的依赖性很小,并且随着塑性变形的增加而逐渐消失。因此,可以使材料的响应完全独立于温度和场变量的历史,通过使用恒定的参数γ k。这可以通过首先运行数据检查分析来实现;在数据检查期间,可以从数据文件中提供的信息确定适当的γ k常数值。参数C k和常数参数γ k的值可以直接输入,如上所述。
当采用多背应力模型时,Abaqus获得不同初始猜测值的硬化参数,并选择与实验数据相关性最好的硬化参数。但是,应该仔细检查获得的参数。在某些情况下,在选择参数集之前获得不同背应力数的硬化参数可能是有利的。
各向同性硬化分量应通过定义零塑性应变下屈服面大小的等效应力以及等效应力随等效塑性应变的演化来定义。如果没有定义这个分量,Abaqus将假设没有循环硬化发生,因此定义屈服面尺寸的等效应力是恒定的,等于(σ 1 + σ n) / 2(或者当提供多个应变范围时,这些量在几个应变范围内的平均值)。由于这个大小与饱和循环的大小相对应,因此不太可能提供对实际行为的准确预测,特别是在初始循环中。
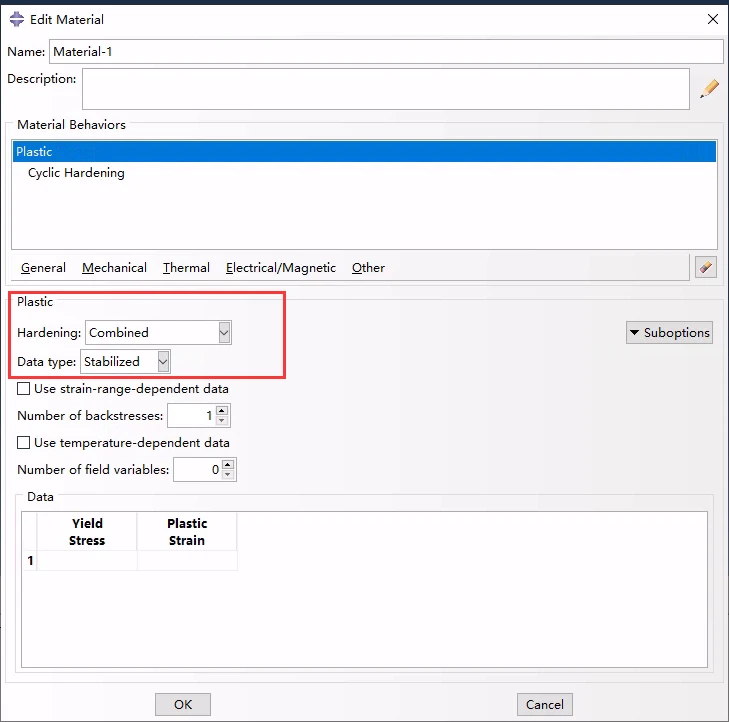
通过指定稳定循环的测试数据来定义运动硬化分量
1.3 多线性随动硬化模型
多线性随动硬化模型可以利用单向拉伸或压缩实验得到的试验数据进行标定。Abaqus通过提供应力-塑性应变数据对来定义这种多线性行为。应力-塑性应变曲线上第k个数据点与(k + 1)个数据点之间的硬化模量H k由关系确定:
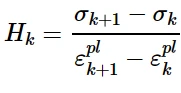
多线性随动硬化模型的硬化模量
通过多线性随动硬化数据很容易理解:
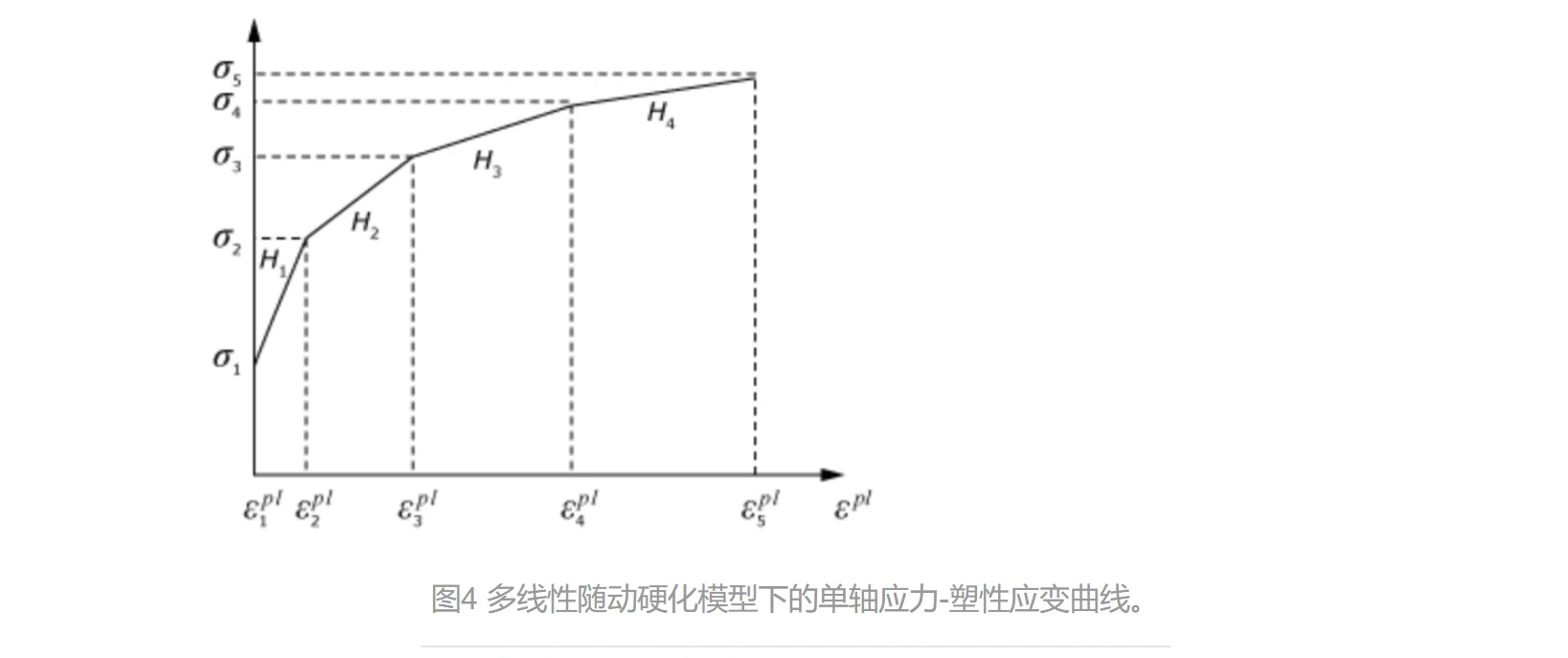
数据对输入应依次提供图中的各点数据
数据应使硬化模量不随塑性应变而增加。用户提供的数据点数量决定子体积的数量N。计算成本和内存需求随着N的增加而增加。因此,用于近似分段线性响应的应力-塑性应变曲线的数据点数量应始终最小化。
可以提供几组数据对,作为温度和/或场变量的函数。但是,必须确保与不同温度和/或场变量对应的数据点或子体积的总数相同。
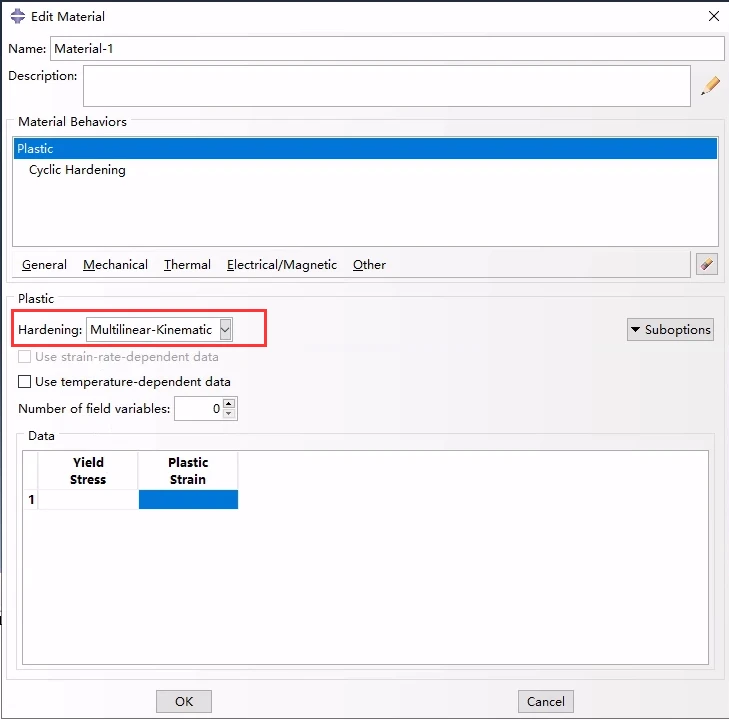
多线性随动硬化模型的CAE定义
2. 初始条件
当我们需要研究已经经过某种硬化的材料的行为时,Abaqus允许规定等效塑性应变的初始条件,¯ε p1,以及在线性运动硬化模型和非线性各向同性/运动硬化模型的情况下的背应力α k。当采用非线性各向同性/运动硬化模型时,每个背应力α k的初始条件必须满足该条件:
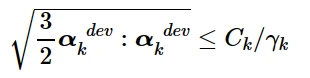
使模型产生随动硬化响应。Abaqus允许指定违反这些条件的初始背应力。然而,在这种情况下,违反条件的背应力对应的响应产生运动软化响应:背应力的大小随着塑性应变从初始值到饱和值而减小。如果任何背应力的条件被违反,材料的整体响应不能保证产生随动硬化响应。采用线性运动硬化模型时,背应力的初始条件不受限制。
可以直接指定¯ε p1和α k的初始值作为初始条件。
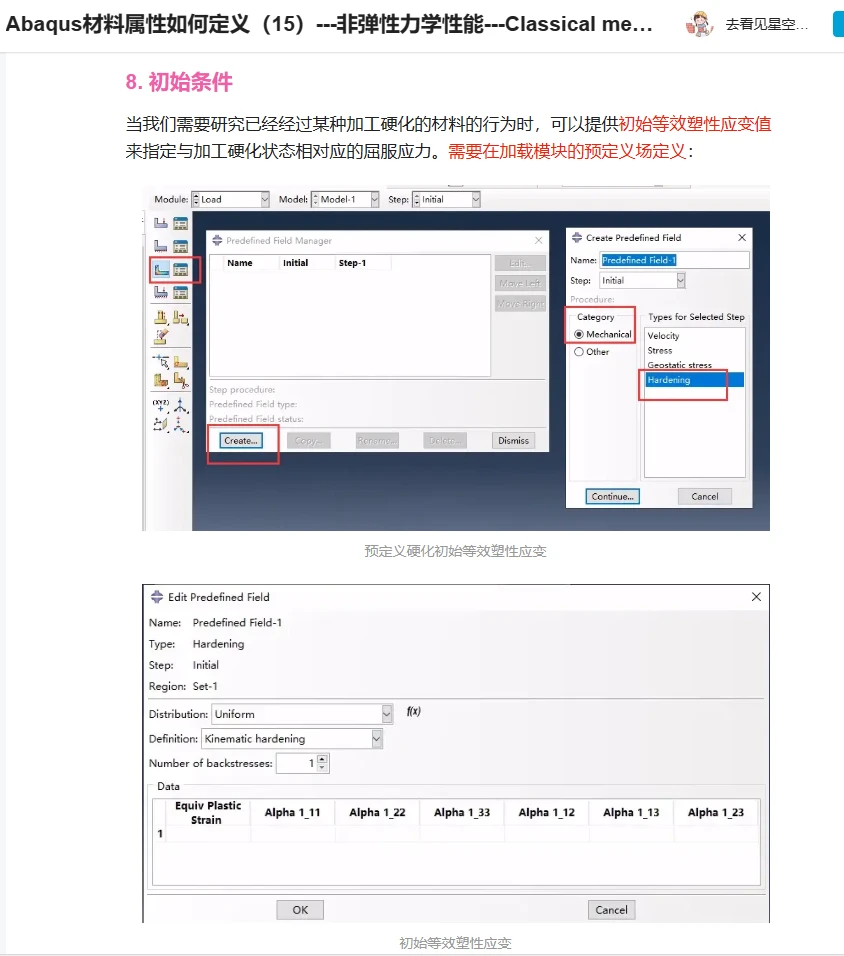
初始条件
3. 单元和输出
线性随动硬化模型和非线性各向同性/随动硬化模型可用于Abaqus/Standard中包含力学行为的单元(具有位移自由度的单元),但空间中的某些梁单元除外。空间中包含由扭转引起的剪切应力(即,不包括薄壁开口截面)和不包括环向应力(即,不包括PIPE单元)的梁单元不能与非线性随动学硬化模型一起使用。在Abaqus/Explicit中,线性随动硬化模型和非线性各向同性/随动硬化模型可以用于包括力学行为的任何单元,当模型与Hill屈服面一起使用时除了一维单元(梁,管道和桁架)。多线性随动硬化模型只能在具有平面应变、广义平面应变、轴对称和三维实体(连续体)单元的Abaqus/Standard中使用。
除了Abaqus中可用的标准输出标识符外,以下变量对随动硬化模型具有特殊意义:
ALPHA:总的运动硬化平移张量分量
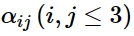
ALPHAk: k th运动硬化平移张量分量(1≤K≤10)
ALPHAN:所有随动硬化平移张量的分量,除了总移位张量。
PEEQ:等效塑性应变
PENER:塑性功,这个量可以在用户子程序UVARM中作为用户定义的输出变量来计算。
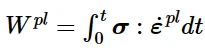
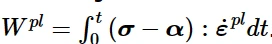
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删