深入Abaqus材料属性的随动硬化模型理论

随动硬化模型：（金属受循环载荷的模型）

用于模拟材料在循环荷载作用下的非弹性行为；

包含线性随动硬化模型，非线性各向同性/随动硬化模型，以及在Abaqus/Standard中的多线性运动硬化模型；

包含具有多个背应力的非线性各向同性/随动硬化模型；

可用于任何具有位移自由度单元的求解；

在Abaqus/Standard中不能用于绝热分析，非线性各向同性/随动硬化模型不能用于温度-位移耦合分析；

除多线性随动硬化外，可用于建立速率相关的屈服；

可与Abaqus/Standard中的蠕变和溶胀一起使用；

要求使用材料的线弹性模型来定义弹性部分的响应。

   随动硬化定义
 

1. 屈服面

用于模拟金属循环加载行为的随动硬化模型是与压力无关的塑性模型；换句话说，金属的屈服与等效压应力无关。模型适用于除空心金属外的大多数经受循环载荷条件的金属。

线性随动硬化模型可以使用Mises屈服面或Hill屈服面。非线性各向同性/随动模型只能与Abaqus/Standard中的Mises屈服面和Abaqus/Explicit中的Mises或Hill屈服面一起使用。线性随动硬化模型和非线性各向同性/随动硬化模型中使用的压力无关屈服面，由函数定义：

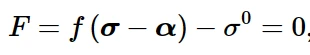
   随动硬化的屈服函数
 

其中σ0为屈服应力，f(σ−α)为相对于背应力α的等效Mises应力或Hill势。

例如，等效Mises应力定义为：

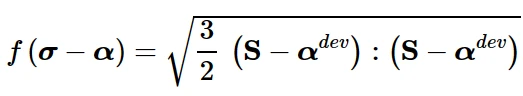
   等效Mises应力
 

其中，S是偏应力张量（定义为S = σ + p I，其中σ为应力张量，p为等效压应力，I 为单位张量)， α dev是背应力张量的偏差部分。

多线性随动硬化模型的响应假定为各种完全弹塑性单元的加权和。其中每个单元也被称为子体积，使用具有不同屈服强度的Mises屈服面。

2. 流动法则

随动硬化模型假定关联塑性流动。只要对微观细节(如由于循环疲劳载荷导致的金属构件断裂所产生的塑性流的局部化)不感兴趣，对于经受循环载荷的金属来说，关联塑性流的假设是可以接受的。

2.1 线性随动硬化模型和非线性各向同性/随动硬化模型

对于线性随动硬化模型和非线性各向同性/随动硬化模型流动法则为:

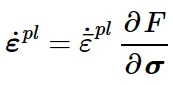
   关联流动 塑性变形方向沿着屈服函数的法线方向
 

其中，˙ε pl为塑性流动速率，˙¯ε pl 为等效塑性应变率。

等效塑性应变的演化由以下等效塑性功表达式得到：

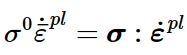
对于各向同性MIses塑性，得到：

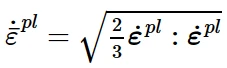
2.2 多线性随动硬化模型

多线性运动硬化模型的流动法则如下:

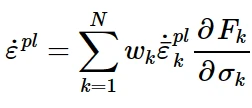
   加权和，依然沿法线方向
 

式中N为子体积总数，w k、F k、˙¯ε pl k和σ k分别为权重、Mises屈服面、等效塑性应变率和第k个子体积的应力。每个子体积都遵循一个相关的流动法则。

3. 硬化

线性随动硬化模型具有恒定的硬化模量，非线性各向同性/随动硬化模型同时具有非线性随动和非线性各向同性硬化分量。多线性随动硬化模型具有分段的恒定硬化模量。

3.1 线性随动硬化模型

该模型的演化规律由线性随动硬化分量组成，该分量描述了屈服面在应力空间中通过背应力α的平移；当忽略温度依赖性时，该演化规律为线性Ziegler硬化规律：

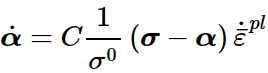
   线性Ziegler硬化规律
 

式中˙¯ε p1为等效塑性应变率，C为随动硬化模量。在该模型中，定义屈服面尺寸的等效应力σ 0保持不变，σ 0 = σ | 0，其中σ | 0为零塑性应变下定义屈服面尺寸的等效应力。

3.2 非线性各向同性/随动硬化模型

该模型的演化规律由两部分组成:非线性随动硬化部分，它描述了屈服面在应力空间中通过背应力α的平移；以及各向同性硬化分量，描述了等效应力的变化。

将运动硬化项定义为纯运动项(线性Ziegler硬化律)和松弛项(recall 项)的叠加，引入了非线性。此外，几个随动硬化成分(背应力)可以叠加，这可能在某些情况下大大改善结果。当忽略温度和场变量依赖关系时，每个背应力的硬化规律为：

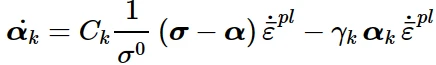
并以此关系式计算总背应力：

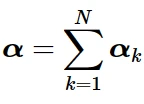
其中N为背应力个数，Ck和γ k为材料参数，必须根据循环试验数据进行校准。Ck为初始随动硬化模量，γ k决定随动硬化模量随塑性变形的增加而降低的速率。随动硬化律可分为偏部分和静水压力部分；只有偏部分对材料性能有影响。当Ck和γ k均为零时，模型简化为各向同性硬化模型。当所有γ k均为0时，简化为线性Ziegler硬化规律。

图1显示了一个具有三个背应力的非线性随动硬化的例子。

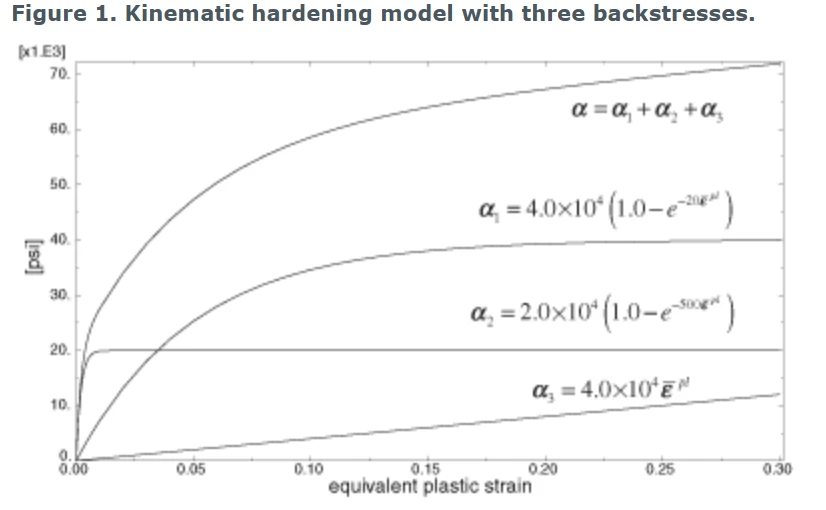
   图1 具有三个背应力的随动硬化模型
 

每个背应力覆盖不同的应变范围，并且对于大应变保留线性硬化规律。

模型的各向同性硬化行为定义了屈服面尺寸σ 0随等效塑性应变¯ε p1的变化规律。这种演化可以通过直接以表格形式将σ 0指定为¯ε p1的函数，或者在用户子程序UHARD中指定σ 0(仅在Abaqus/Standard中)，或者使用简单指数定律来引入：

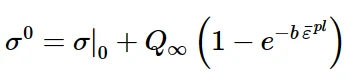
   指数硬化
 

其中σ | 0为零塑性应变时的屈服应力，Q∞和b为材料参数。Q∞表示屈服面尺寸的最大变化量，b表示屈服面尺寸随塑性应变的变化率。当定义屈服面尺寸的等效应力保持不变(σ 0 = σ | 0)时，模型简化为非线性随动硬化模型。

单向加载和多轴加载的各向同性/随动硬化分量的演变如图2和图3所示。

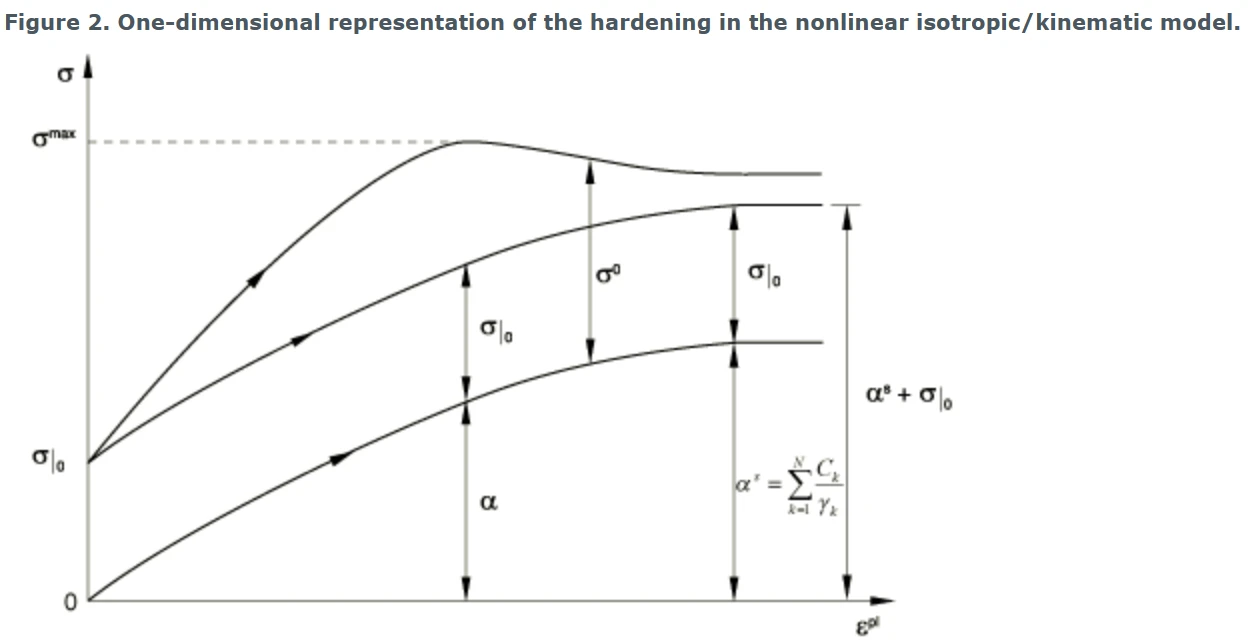
   图2 非线性各向同性/随动硬化模型中硬化的一维表示。
 

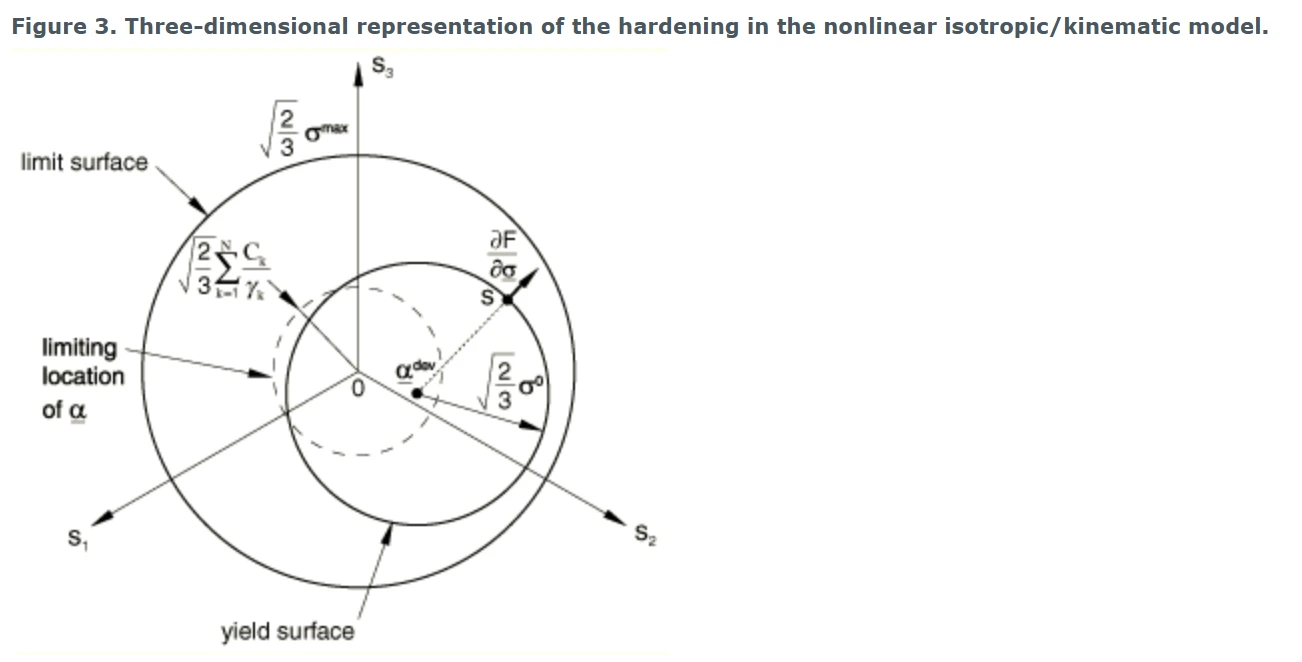
   图3 非线性各向同性/随动模型中硬化过程的三维表示。
 

随动硬化分量的演化规律表明，背应力包含在半径为

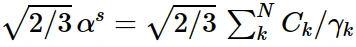
的圆柱体内，其中α s为饱和时(大塑性应变)α的量级。它还意味着任何应力点必须位于半径为

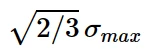
的圆柱体内(使用图2的符号)，因为屈服面仍然是有界的。在大塑性应变下，任何应力点都包含在半径为

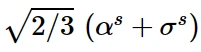
的圆柱体内，其中σ s是定义大塑性应变下屈服面大小的等效应力。如果表格提供了各向同性分量数据，则σ s是定义屈服面大小的最后一个值。如果使用用户子例程UHARD，该值将取决于自己的定义;否则，σ s = σ | 0 + Q∞。

3.3 多线性随动硬化模型

通过将单轴屈服应力值作为单轴塑性应变的函数来定义多线性运动硬化模型(图4)。

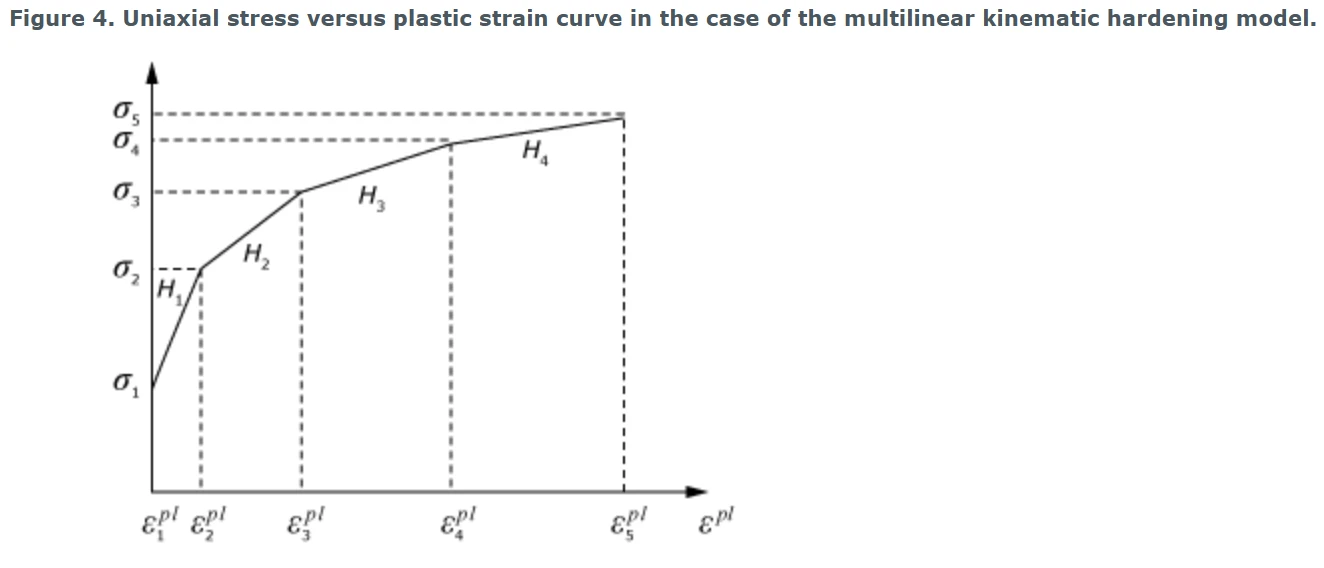
   图4 多线性随动硬化模型下的单轴应力-塑性应变曲线。
 

输入曲线上给出的应力-塑性应变对数决定了模型中的子体积数N。第k个子体积(σ y, k)的屈服强度计算为

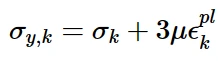
其中

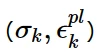
为用户指定的应力-塑性应变数据，μ为材料的剪切模量。所有子体承受相同的总应变，总应力计算为各子体应力的加权和:

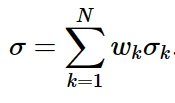
第k个子体积的权值是：

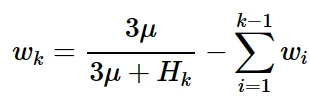
其中，H k为应力与塑性应变曲线上第k个数据点与(k +1)个数据点之间的硬化模量。所有子体积的权重之和是1。假定硬化模量在最后一个数据点之后为零。

4. 预测材料性能

在随动硬化模型中，由于随动硬化分量的作用，屈服面中心在应力空间中移动。此外，当采用非线性各向同性/随动硬化模型时，由于各向同性分量的存在，屈服面范围可能会扩大或缩小。这些特性允许对受载荷或温度循环影响的金属的非弹性变形进行建模，从而导致显著的非弹性变形和可能的低周疲劳失效。这些模型可以解释以下现象：

4.1 包辛格效应Bauschinger effect

这种效应的特点是在初始加载期间发生塑性变形后，加载逆转时屈服应力降低。这种现象随着循环的继续而减少。线性随动硬化分量考虑了这种影响，但非线性分量改善了循环的形状。采用具有多个背应力的非线性模型可以进一步改善循环的形状。多线性运动硬化模型也可以用来模拟这种效应。

4.2 循环硬化与塑性安定  Cyclic hardening with plastic shakedown

这种现象是对称应力或应变控制实验的特性。软的或退火的金属趋向于向稳定的极限硬化，而最初硬化的金属又趋向于软化。图5显示了金属在指定的对称应变循环下的硬化行为。

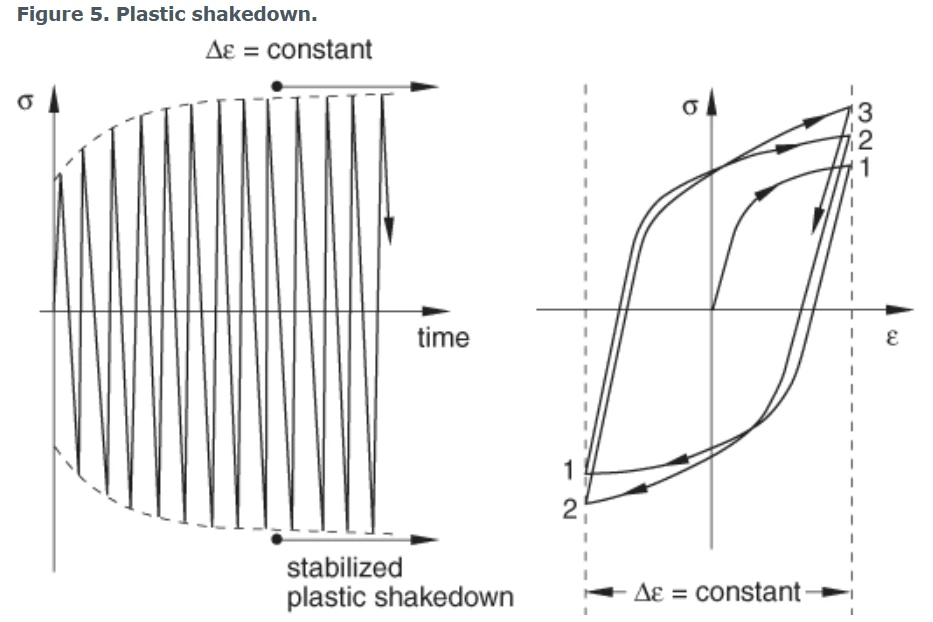
   图5 Plastic shakedown
 

模型的运动硬化分量单独用于预测一个应力循环后的塑性安定。各向同性分量与非线性随动分量的结合可以预测几个周期后的安定性。

4.3 棘轮效应Ratchetting

在指定极限之间的不对称应力循环将导致在平均应力方向上渐进的“蠕变”或“棘轮”

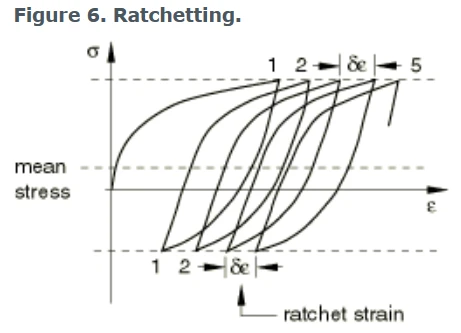
   棘轮效应Ratchetting
 

通常，在低平均应力下，瞬态棘轮紧跟着稳定化(零棘轮应变)，而在高平均应力下，观察到累积的棘轮应变不断增加。非线性随动硬化分量，不使用各向同性硬化分量时，预测恒定的棘轮应变。加入各向同性硬化可以改善棘轮应变的预测，在各向同性硬化的情况下，棘轮应变可以减小，直到达到恒定。然而，一般情况下，单一背应力的非线性硬化模型预测的棘轮效应过于显著。通过叠加多个随动硬化模型(背应力)并选择其中一个模型为线性或接近线性(γ k≪C k)，可以大大改善棘轮的建模效果，从而使棘轮效应不那么明显。多线性随动硬化模型无法预测这种效应。

4.4 平均应力的松弛 Relaxation of the mean stress

这种现象是不对称应变实验的特征，如图7所示。

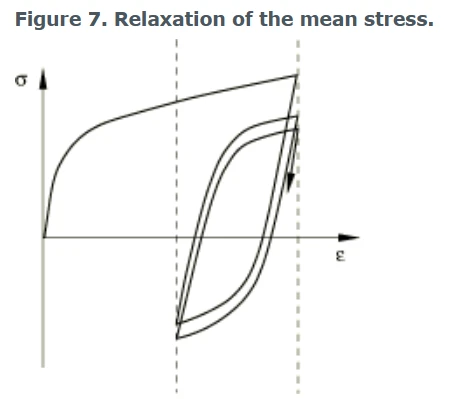
   图7 平均应力的松弛
 

随着循环次数的增加，平均应力趋于零。非线性各向同性/随动硬化模型的非线性随动硬化分量可以解释这种行为。

5. 局限性

线性随动模型是一种简单的模型，它只给出了金属在循环载荷下的初步近似，如上所述。非线性各向同性/随动硬化模型可以在许多涉及循环加载的情况下提供更准确的结果，但仍存在以下局限性：

各向同性硬化在所有应变范围内都是相同的。然而，物理观察表明，各向同性硬化的量取决于应变范围的大小。此外，如果试样在两个不同的应变范围内循环，一个接一个，第一个循环的变形影响第二个循环的各向同性硬化。因此，该模型只是实际循环行为的粗略近似。它应该被校准到在应用中重要的应变循环的预期尺寸。

在比例和非比例荷载循环下，预测了相同的循环硬化行为。物理观察表明，在相似的应变幅下，材料在非比例加载下的循环硬化行为可能与单轴行为大不相同。

简单的比例和非比例循环试验、循环加载下的缺口梁、拉压缩下的单轴棘轮等实例问题，说明了非线性各向同性/随动硬化模型的塑性失稳、棘轮、平均应力松弛等循环硬化现象及其局限性。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删