关于延性金属损伤与失效的渐进式损伤与失效模型是Abaqus中材料损伤与失效建模的推荐方法;这些模型适用于准静态和动态情况。Abaqus/Explicit还提供了两个额外的单元破坏模型,仅适用于高应变率动态问题。剪切失效模型由塑性屈服驱动。拉伸失效模型是由拉伸载荷驱动的。一旦达到应力极限,这些破坏模型可用于限制单元的后续承载能力(直到移除单元点)。两种模型可以用于相同的材料。
剪切失效模型:
用于高应变率变形的许多材料,包括大多数金属;
采用等效塑性应变作为失效度量;
故障发生时提供两种选择,包括从网格中删除单元;
可以与Mises 或 Johnson-Cook 塑性模型结合使用;
可与拉伸失效模型结合使用。
拉伸失效模型:
用于高应变率变形的许多材料,包括大多数金属;
采用静水压应力作为失效度量来模拟动态碎裂或压力切断;
故障发生时提供多种选择,包括从网格中删除单元;
可以与Mises 或 Johnson-Cook 塑性模型,状态方程结合使用;
可与剪切失效模型结合使用。
1. 剪切失效模型
剪切破坏模型可与Abaqus/Explicit中的Mises或Johnson-Cook塑性模型结合使用,以定义材料的剪切破坏。
1.1 剪切失效准则
剪切失效模型基于单元积分点的等效塑性应变值;当损伤参数超过1时假定发生破坏。损伤参数ω定义为:
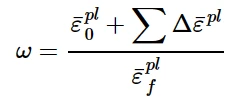
剪切损伤参数
其中:
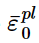
¯ε pl 0为等效塑性应变的任意初始值

Δ¯ε pl为等效塑性应变的增量
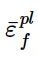
¯ε pl f为破坏时的应变
假设破坏时的应变为¯ε pl f,取决于塑性应变率˙¯ε pl、无量纲压力-偏应力比 p / q(其中p为压应力,q为米塞斯应力)、温度、以及预定义场变量。有两种方法定义失效时的应变:一种是直接使用表格数据,其中依赖项以表格形式给出。或者,可以调用Johnson-Cook提出的分析形式。
当使用直接表格数据来定义剪切破坏模型时,破坏时的应变(¯ε pl f)必须作为等效塑性应变率、压力与偏应力比、温度和预定义场变量的表格函数给出。这种方法需要使用Mises塑性模型。
对于Johnson-Cook剪切破坏模型,必须指定破坏参数d1 - d5;剪切破坏数据必须在或低于转变温度,θtransition,这种方法需要使用Johnson-Cook塑性模型。

通过输入文件指定剪切失效模型

剪切失效模型数据的指定-通过输入文件
1.2 单元删除
当某一积分点满足剪切失效准则时,则将所有应力分量设为零,该材料点破坏。默认情况下,如果一个单元的任何一个截面的所有材料点都失效,则该元素将从网格中删除;不需要单元中所有材料点都失效。例如,在一阶减缩积分的实体单元中,一旦单元的唯一积分点失效,则单元被移除。然而,在壳单元中,所有贯穿厚度的积分点必须都失效才会从网格中移除单元。在二阶减积分梁单元的情况下,在沿梁轴的两个单元积分位置的任何一个处,所有积分点的破坏都会默认导致单元删除。类似地,在修正的三角形和四面体实体单元中,默认情况下任何一个积分点的破坏都会导致单元删除。元素删除是默认的失效选择。
另一种不删除单元的失效选择是,指定当在一个材料点满足剪切破坏准则时,该点的偏应力分量将被设置为零,并在后续计算保持为零。要求压应力保持压缩,也就是说,如果在增量中的失效材料点中计算压应力为负,则将其重置为零。当使用平面应力、壳、膜、梁、管和桁架单元时,这种失效选择是不允许的,因为可能会违反结构约束。

使用输入文件指定是否选择单元删除方法
1.3 适用性
Abaqus/Explicit中的剪切失效模型适用于惯量较大的高应变率动态问题。剪切失效模型使用不当可能导致模拟结果不正确。
对于可能需要删除单元的准静态问题,建议使用渐进损伤和破坏模型(progressive damage and failure)或Gurson多孔金属塑性模型。
2. 拉伸失效模型
拉伸失效模型可以与Mises或Johnson-Cook塑性模型或Abaqus/Explicit中的状态方程材料模型结合使用,以定义材料的拉伸破坏。
2.1 拉伸失效准则
Abaqus/Explicit拉伸失效模型使用静水压应力作为破坏度量来模拟动态剥落或压力切断。拉伸失效准则假定,当压应力p大于用户指定的静水断裂应力σ cutoff 时发生破坏。静水断裂应力可能是温度和预定场变量的函数。该压力没有默认值。

通过输入文件指定拉伸失效准则

拉伸失效模型数据的指定-通过输入文件
2.2 失效选择
当单元积分点满足拉伸破坏准则时,材料点失效。对于失效的材料点,提供了五种失效选择:默认选择元素删除,以及四种不同的破碎模型。下面描述了这些失效选择:
单元删除:
当某一积分点满足拉伸失效准则时,所有应力分量设为零,该材料点失效。默认情况下,如果一个单元的任何一个截面的所有材料点都失败,则该单元将从网格中移除,无需单元中的所有材料点都失效。例如,在一阶减缩积分的实体单元中,一旦单元的唯一积分点失效,单元就会被移除。然而,在壳单元中,所有贯穿厚度的积分点必须在单元从网格中删除之前都失效。在二阶减积分梁单元的情况下,在沿梁轴的两个单元积分位置的任何一个处,所有积分点的破坏导致单元删除。类似地,在修正的三角形和四面体实体单元中,默认情况下在任何一个积分点的破坏都会导致单元删除。

通过输入文件指定使用单元删除失效方法
其他选择:The spall models
另一种失效选择是基于剥落(材料的破碎),而不是单元的移除。在此类别中有四种失效组合。当某一材料点满足拉伸失效准则时,偏应力分量可能不受影响,也可能被要求为零;压应力可能受到静水断裂应力的限制,也可能被要求为可压缩。因此,有四种可能的失效组合(见图1,其中“O”表示不使用拉伸失效模型时将会存在的应力)。
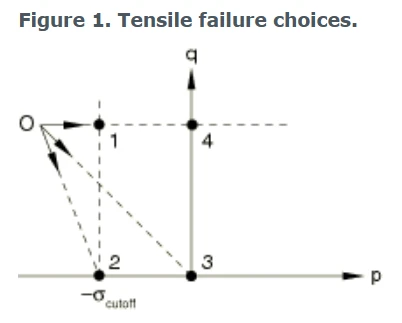
拉伸失效选择
这些失效组合如下:
① 韧性剪切和韧性压力:此选择对应于图1中的点1,并模拟了偏应力分量不受影响且压应力受静水断裂应力限制的情况,即,p = m a x (- σ cutoff,p)。

定义方法
② 脆性剪切和韧性压力: 该选择对应于图1中的点2,并模拟了偏应力分量设为零并在后续计算中保持为零,压应力受静水断裂应力限制的情况,即,p = m a x (- σ cutoff,p)。

定义
③ 脆性剪切和脆性压力:
此选择对应于图1中的点3,并模拟将偏应力分量设为零并在后续计算中保持零的情况,并且要求压应力为可压缩的,即,p = m a x (0, p)

定义
④ 韧性剪切和脆性压力:此选择对应于图1中的点4,并模拟了偏应力分量不受影响且要求压应力为可压缩的情况,即,p = m a x (0, p)

定义
综上,对于剥落模型没有默认的失效组合。如果选择不使用单元删除,则必须显式指定失效组合。如果没有定义材料的偏应力行为(例如,使用没有偏应力行为的状态方程模型),则组合中的偏差部分是没有意义的,将被忽略。平面应力、壳、膜、梁、管、桁架单元不允许使用剥落模型(The spall models)。
2.3 适用性
Abaqus/Explicit中的拉伸失效模型适用于考虑惯性效应的高应变率动态问题。使用不当的拉伸破坏模型可能导致不正确的模拟。
3. 单元和输出
删除单元的剪切和拉伸失效模型可用于Abaqus/Explicit中包含力学行为(具有位移自由度的单元)的任何单元。在Abaqus/Explicit中,不删除单元的剪切和拉伸失效模型只能用于平面应变、轴对称和三维实体(连续体)单元。
除了Abaqus/Explicit中提供的标准输出标识符之外,以下变量对于剪切和拉伸失效模型具有特殊意义:
STATUS:单元的状态;(如果元素有效,则元素的状态为1.0,如果元素失效,则为0.0)。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删