本系列文章研究成熟的有限元理论基础及在商用有限元软件的实现方式,通过
1) 基础理论
2) 商软操作
3) 自编程序
三者结合的方式将复杂繁琐的结构有限元理论通过简单直观的方式展现出来,同时深层次的学习有限元理论和商业软件的内部实现原理。
有限元的理论发展了几十年已经相当成熟,商用有限元软件同样也是采用这些成熟的有限元理论,只是在实际应用过程中,商用CAE软件在传统的理论基础上会做相应的修正以解决工程中遇到的不同问题,且各家软件的修正方法都不一样,每个主流商用软件手册中都会注明各个单元的理论采用了哪种理论公式,但都只是提一下用什么方法修正,很多没有具体的实现公式。商用软件对外就是一个黑盒子,除了开发人员,使用人员只能在黑盒子外猜测内部实现方式。

一方面我们查阅各个主流商用软件的理论手册并通过进行大量的资料查阅猜测内部修正方法,另一方面我们自己编程实现结构有限元求解器,通过自研求解器和商软的结果比较来验证我们的猜测,如同管中窥豹一般来研究的修正方法,从而猜测商用有限元软件的内部计算方法。我们关注CAE中的结构有限元,所以主要选择了商用结构有限元软件中文档相对较完备的Abaqus来研究内部实现方式,同时对某些问题也会涉及其它的Nastran/Ansys等商软。为了理解方便有很多问题在数学上其实并不严谨,同时由于水平有限可能有许多的理论错误,欢迎交流讨论,也期待有更多的合作机会。
==谐响应分析原理==
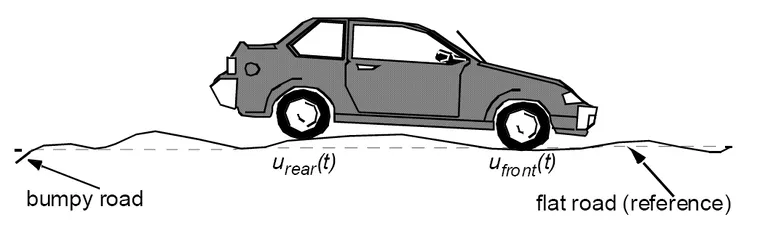
振动分为自由振动和受迫振动,自由振动一般是力加载后释放以后的振动。而受迫振动是一种常见的物理现象,指系统在随时间变化的激励作用下产生的振动。譬如不平整路面对坐在车里的人的颠簸,地震时对建筑物的摇摆震荡。作用在系统上的激励,按它们随时间变化的规律,可以分为简谐激励、一般周期激励和随时间任意变化的非周期性激励。而其中简谐激励在实际工程中应用最广。简谐激励在经过一段过渡过程后,将进入稳态振动过程,称为系统稳态过程,在Abaqus称为稳态动力学Steady State Dynamics,在很多书中还将随机响应也作为稳态动力学的一个分支,为了避免误解,我们这儿将简谐激励作用下的稳态响应称为谐响应分析。由于谐响应分析在振动试验中相对容易实现,且能体现系统的固有特性,因此在工程应用的也非常广泛。本文将简单介绍一下谐响应的原理和试验过程,同时利用iSolver和Abaqus计算一个悬臂梁的谐响应分析例子来说明谐响应和模态频率的关系。

对一个简单的单自由度弹簧系统来说,
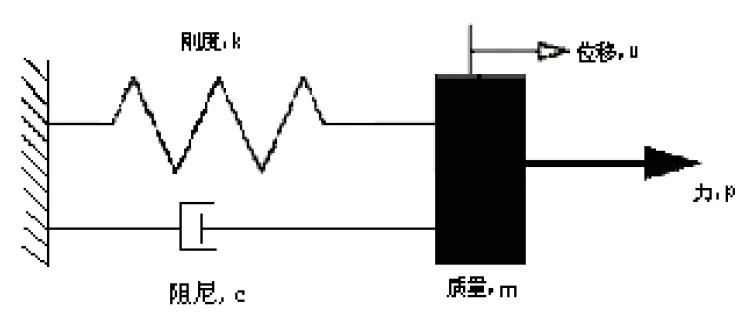

根据牛顿第二定律,内外力平衡:
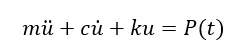

其中,m、c、k分别是弹簧质量、阻尼和刚度。
如果外力是简谐力,那么P可以表示为:
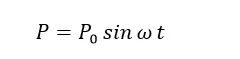

也就是激励随时间变化如下:

假定取模态阻尼,此时阻尼可以表示为:
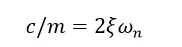
那么得到单自由度的位移随时间t的变化如下:

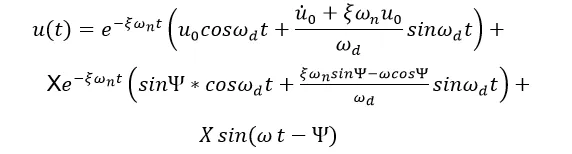


其中
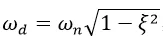
 ,使得前两行与输入频率无关,只与模型的自由振动有关,而这种自由振动会随着时间迅速做e指数衰减。
,使得前两行与输入频率无关,只与模型的自由振动有关,而这种自由振动会随着时间迅速做e指数衰减。
第三项与输入频率相关,且没有衰减项,将伴随着输入载荷一直振动下去。由于实际系统中不可避免地存在阻尼,前两项表示的自由振动将会很快被衰减,都是暂态响应,经过一段时间后,系统就只有稳态响应了,所以工程上更关心系统的稳态响应。
譬如在Abaqus里做一个单自由度弹簧,


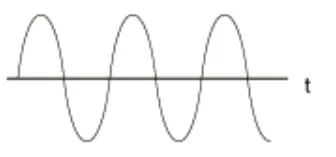
取输入频率=10*固有频率,将位移随时间的变化曲线画出来,如下图所示:
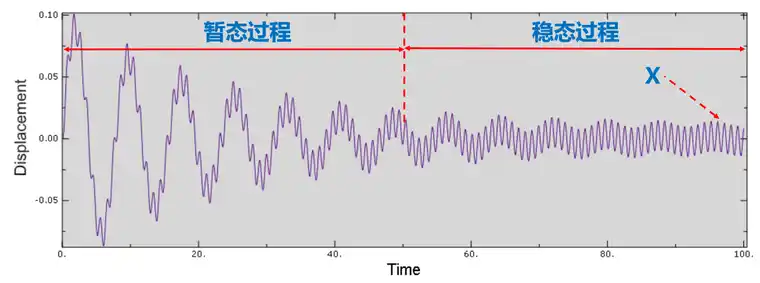

前面部分为暂态过程,此时自由振动占主体,振幅较大,后面部分一个稳态过程,此时按输入频率做正弦振荡,它的幅值就是X。
上面分析的是载荷在某个输入频率的问题,在这个频率下可得到稳定过程的幅值X,这个幅值往往决定你的结构的应力大小,幅值越大,应力也越大,此时结构就相对危险,所以,工程上主要校核两个方面:
1) 这个幅值X和输入之间的放大比例。
2) 这个幅值X导致的应力是否超过结构的许用应力。
X随频率变化,如果在共振点附近,显然这个放大比例和应力也更大,也更容易引起破坏,实际问题中,载荷的频率有可能在一个范围内变化,譬如你的某个旋转机械的转速不同而导致载荷频率也不同,因此我们需要分析根据你的实际载荷的可能频率范围或者设计规范的X的分布情况,此时,我们计算结构在正弦周期载荷作用下对每一个计算频率点的动态响应,也就是谐响应分析,有些地方也称为正弦响应分析、频率响应分析(简称频响分析)、扫频分析等。
譬如上图计算了一个频率点对应的X,将这个扫频范围内的频率分成多个频率点,然后分别计算每个频率点的X,画出曲线,就是一个谐响应曲线了。(注意,不是上面那个图形的FFT变换)

在这个曲线上根据共振峰可以判断系统的固有频率,譬如上面明显85Hz、110Hz、130Hz是系统的固有频率。
同时,为了查看应力,需要对比每个频率点下的最大应力是否满足许用应力校核规范,此时,应力除了和你的频率有关外,还和你在该频率下的输入载荷大小有关,你的载荷的大小根据实际情况也可能不一致,所以需要输入载荷随着时间/频率的一个变化范围。同时载荷随方向旋转可以通过两个方向的加载来实现。
系统谐响应是很容易用振动试验台测出来的,试验的过程和谐响应的定义完全一致:(1)先将系统实物固定在振动台上。


2)根据规范,设置试验规范中上下限频率及间隔,扫描时间等。
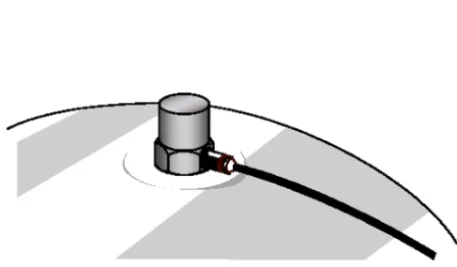
3)先在X方向加载荷振荡,载荷固定为第一个频率点F1,振动台激励持续一段时间达到稳态(想象一下弹簧的受迫振动的稳定状态),然后再测试该频率下的最大响应X1。振动过程类似下方动画:

(上述模型来源于技术邻郑钧老师)
在进行结构试验时,位移相对难测量,所以,一般在关心的重要器件上面装加速度器测量试验模型加速度反应,之后通过软件做FFT或类似的谱分析,可以得到模型频域内的响应。这对应了有限元分析中很多时候看结构的加速度响应。同时,由于测试时需要安装测试仪器,在表面布线,想想看我们看到的航天器外面的线,所以模拟的时候需要加附加质量。
3)将频率变为F2,稳定后继续测试最大响应X2。
4)以此类推,将所有测到的X和F的关系画在一张曲线上就是谐响应曲线。
5)实际问题的载荷如果是多个方向的,此时就需要换Y,Z方向继续测试。
6)同时,因为实际过程可能还需要在前后加入校核载荷,所以可能如下测试:
x方向:校核载荷-->正弦-->校核载荷
y方向:校核载荷-->正弦-->校核载荷
z方向:校核载荷-->正弦-->校核载荷
第一个校核载荷测试一次性能,第二个校核载荷再次测试性能,如果和前一次一样,表面试验没有损坏器件。
谐响应定义和试验中都是在各个频率点振荡达到稳定后再测试最大响应,在有限元分析中,没必要这么做,因为最大响应X如下有明确和频率F的关系式,如下式:只要利用刚度矩阵K、阻尼矩阵C、质量矩阵M就能直接计算得到。


同时,有限元的谐响应分析总是只算出上述的X,但按照谐响应分析的定义,理论上讲只有存在阻尼时,振动稳态振幅才是X的表达式。所以,如果你在有限元中没有设置阻尼,算出来的其实不是真正稳态的解,当没有阻尼时,由谐响应的公式,前面两项e指数衰减项就不能约去,也就是真正稳态的解也应该包括自由振动项。
为了验证谐响应的含义,我们做了一个简单的I型截面的悬臂梁的例子,模型参数如下:


几何:悬臂梁长1000,I型截面参数如下,厚度都是5:
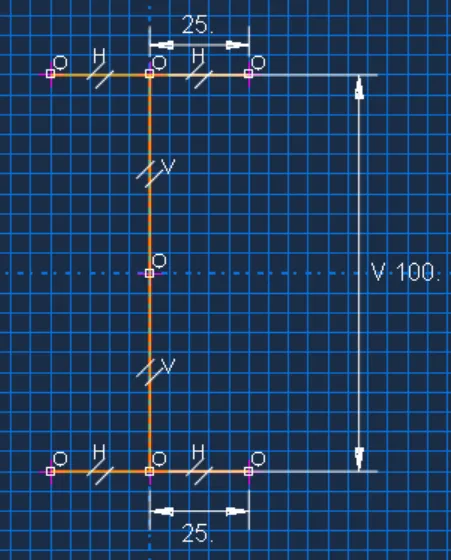

材料:杨氏模量210000,泊松比0.3,密度7.85e-9。
网格:取S4R单元类型,网格大小为12.5。


左端约束:

我们采用Abaqus和iSolver两个求解器分别计算。
第一步,设置模态分析步,选择只计算5个模态。
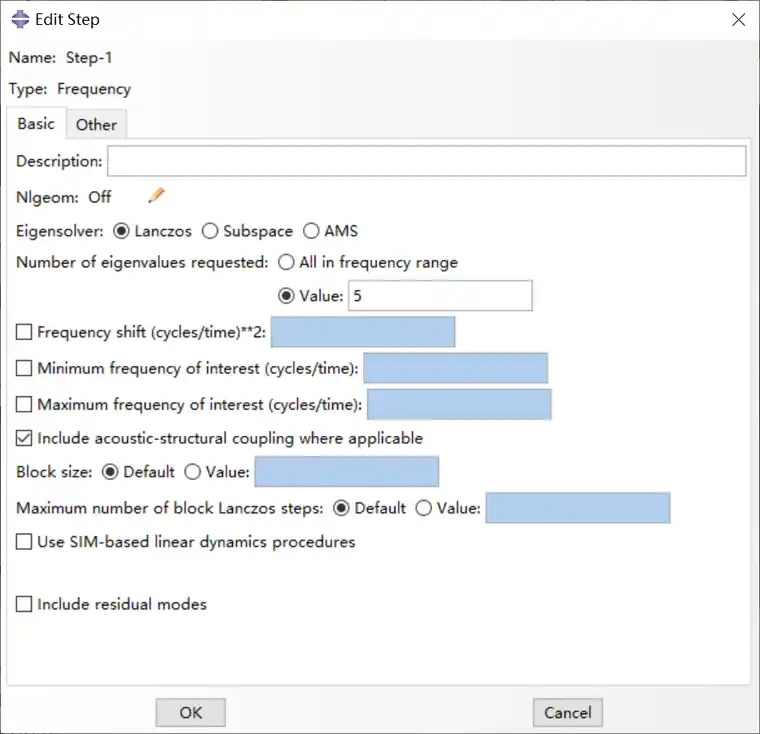

分别调用Abaqus和iSolver求解器,计算完毕后导入Abaqus查看结果。
5阶模态分别如下(左侧是Abaqus结果,右侧为iSolver结果,结果无任何误差)
第一阶是X方向弯曲振型
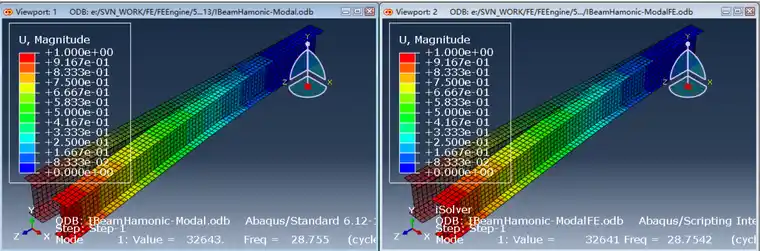

第二阶是Z方向扭转
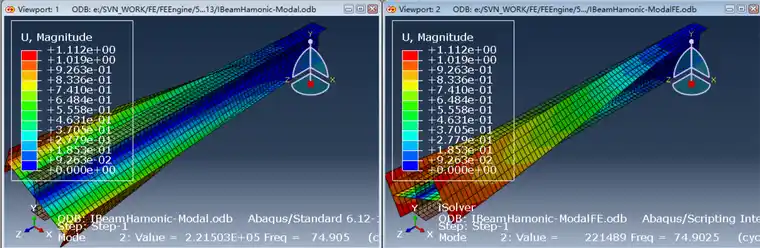

第三阶是Y方向弯曲,频率为115.28
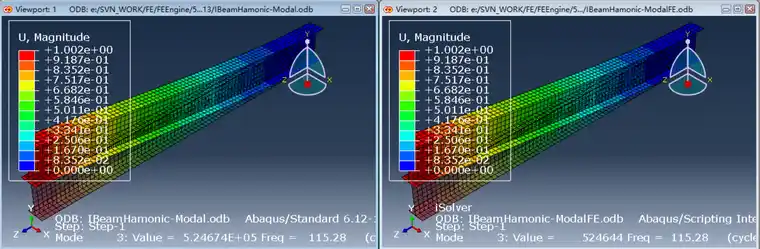

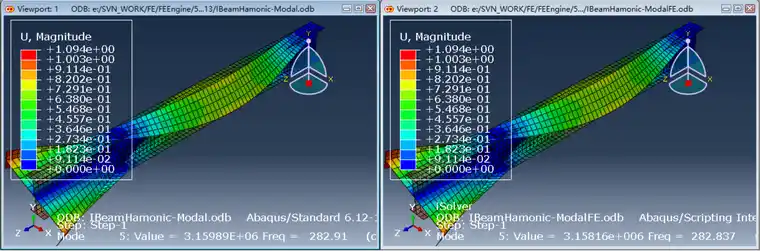
第四阶是X方向弯曲


第五阶是Z方向扭转,频率超出了250Hz。

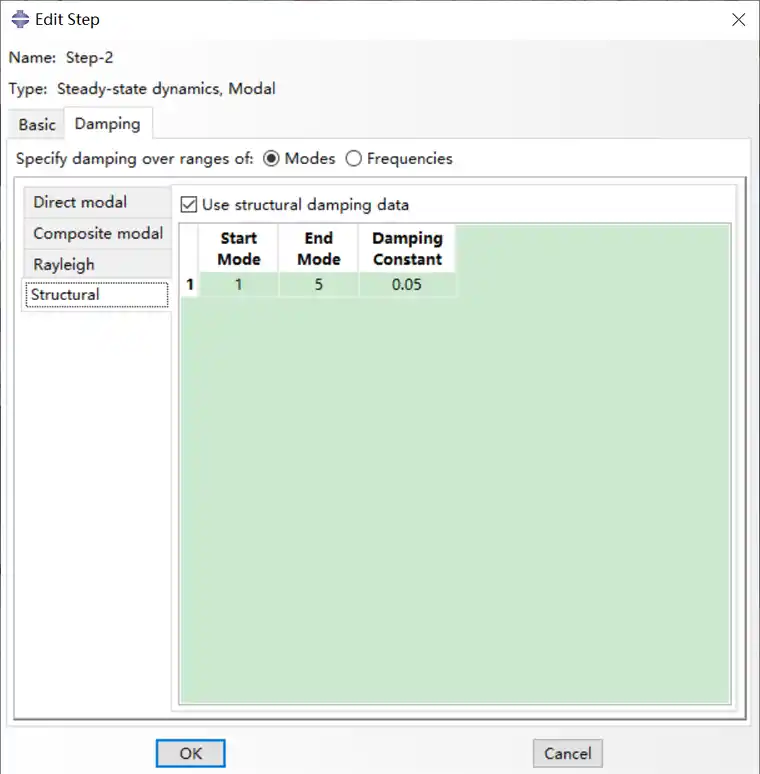
在Abaqus中设置谐响应分析Stead-State dynamics,Modal,频率范围如下:


设置结构阻尼:0.05:

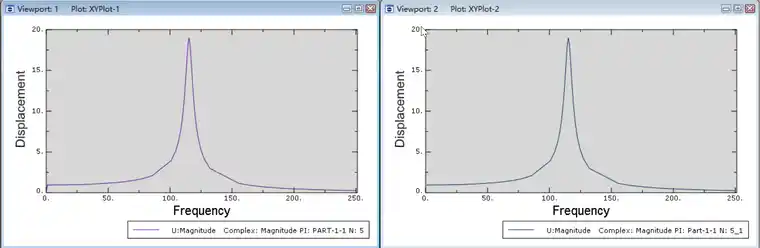
设置载荷:另一端加Y方向载荷方向1000


查看载荷节点在Y方向的谐响应振幅曲线如下:(左侧是Abaqus结果,右侧为iSolver结果,结果无任何误差),可发现在0-250Hz的频率范围内,只有一个共振峰115Hz,由上面的模态分析可知,只有模态3的振动是在Y方向,且是115Hz,因此,谐响应分析只激发了模态3的振动,其它方向的模态没有激发起来。

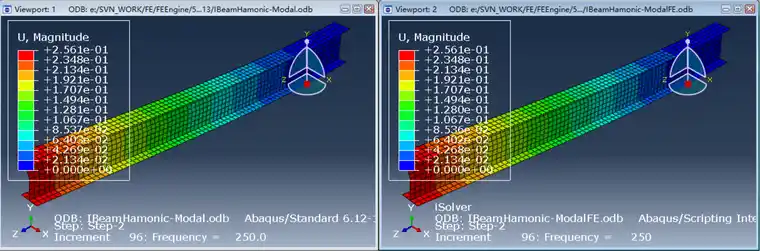
最后一个频率的最大响应位移分布如下,可见iSolver和Abaqus也是没有误差:

如果觉得上面的文字太复杂,也可以看一下视频的简要讲解,包括基于Abaqus和iSolver的操作验证,地址如下:
https://www.jishulink.com/college/video/c12884 20


免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删