Abaqus壳单元几何非线性验证实例

板壳单元是有限元中应用广泛而又具有难度的单元类型，其在相当一段时间内是计算力学研究者广泛研究的对象。常见的有K J bathe的MITC壳单元，龙驭球院士的广义协调壳单元，Belytschko的belytschko-tsay壳单元等。壳单元在几何非线性下的响应评估准确度和计算效率，是有限元软件几何非线性计算能力的重要体现。
 

本文演示一个壳单元几何非线性验证算例的abaqus操作。后续还可能采用其他软件进行该模型及其他几个壳单元几何非线性的验证对比。

模型具体信息：

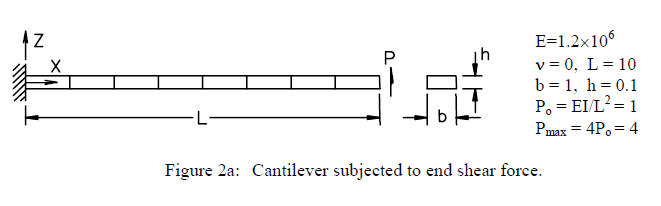
具体待验证的结果：

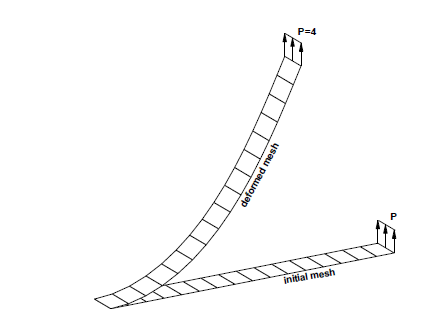
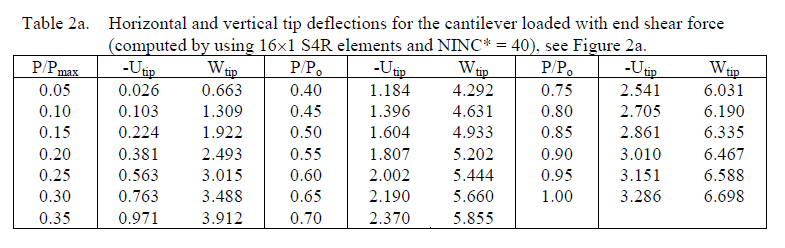
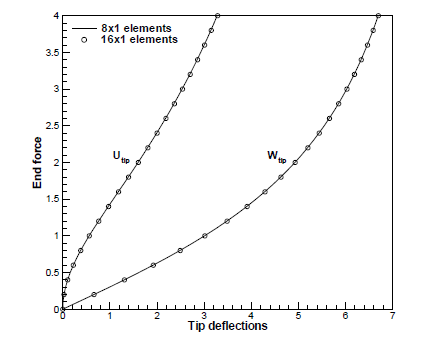
操作过程：

1. 建立3D shell part，进入草图后绘制矩形，矩形尺寸为长10宽1

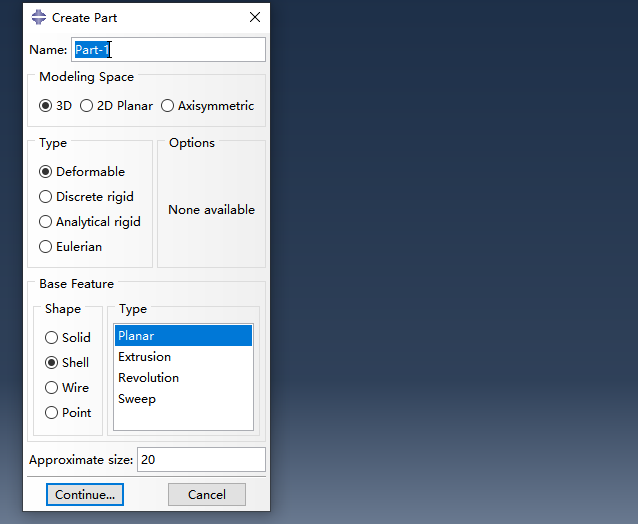
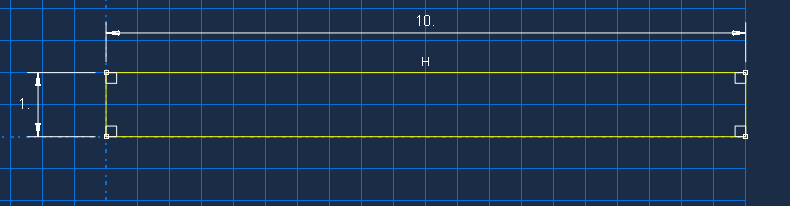
2.进入property模块

2.1 创建材料：

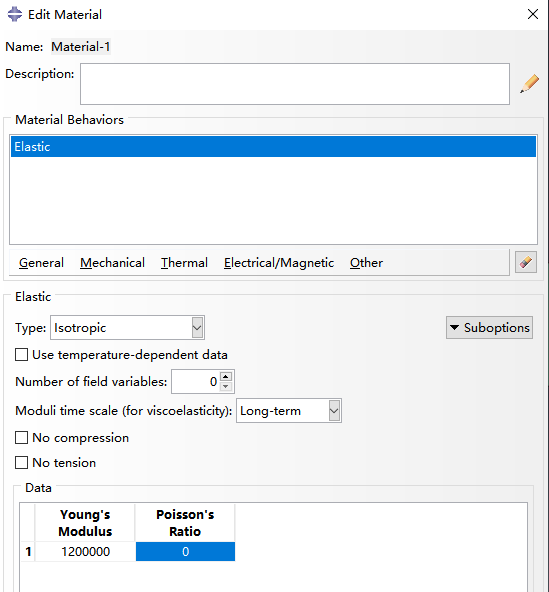
2.2 创建截面，截面类型选shell-homogeneous，在edit section设置thick为0.1，材料选择之前创建的material-1

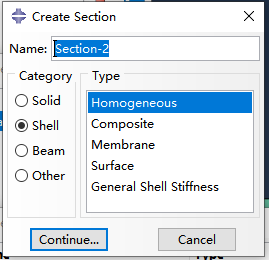
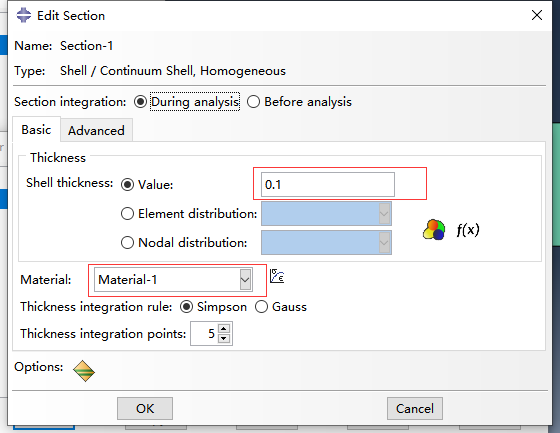
2.3完成截面指定

3 进入Assembly模块，装配模型

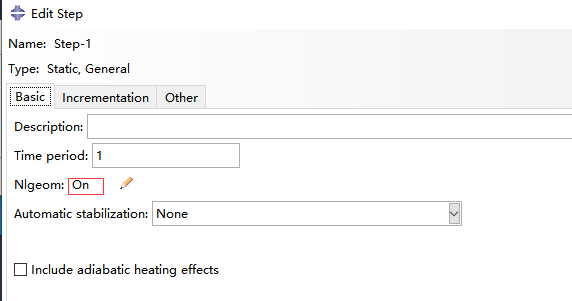
4  进入step模块，创建static-general step，打开Nlgeom，同时总步数，初始增量，最小增量，最大增量分别设置为200，0.05，1.0e-5，1；

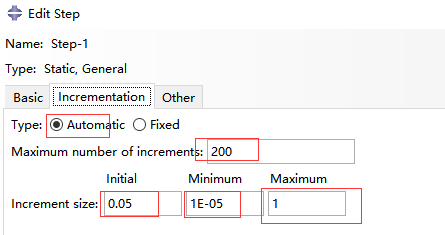
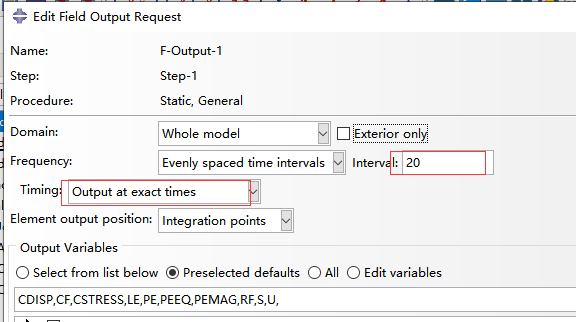
进入field output manager，edit，设置输出间隔（此步保证每隔0.05增量输出一次结果，方便与上面表中的结果对照）：

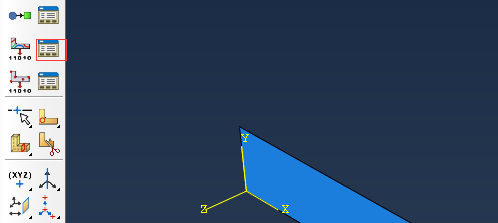
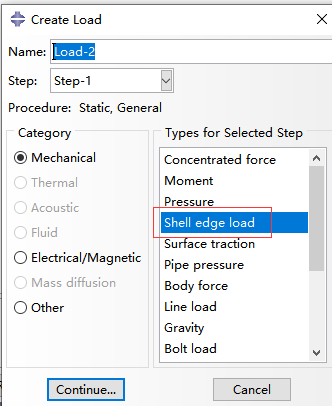
5）进入load模块，对模型一侧施加固定约束，另一侧施加shell edge load

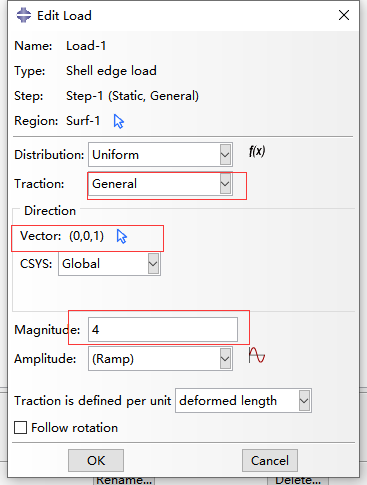
进入edit load菜单后traction 选择General，点击Vector后的箭头，分别输入方向向量的第一点 和第二点 为(0,0,0)和(0,0,1)，在Magnitude输入4。

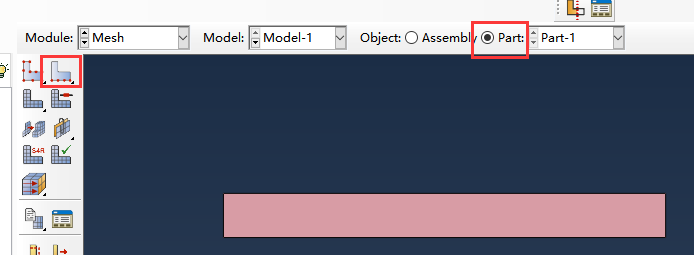
进入mesh模块，分别对矩形的两条边设置划分段数为16和1，再进行网格划分

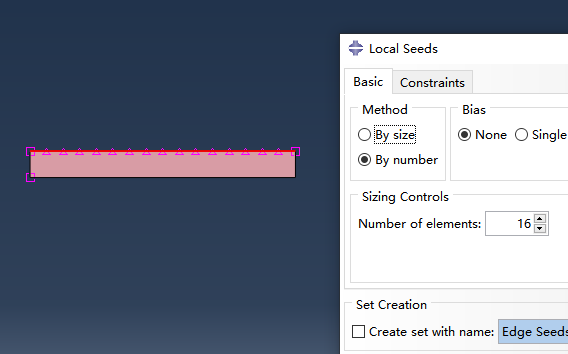
创建JOB提交

后处理显示位移云图

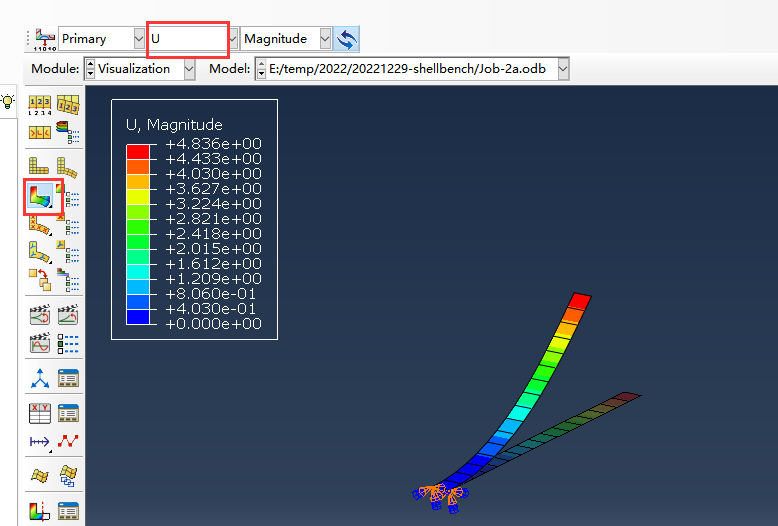
提取反力-位移曲线：

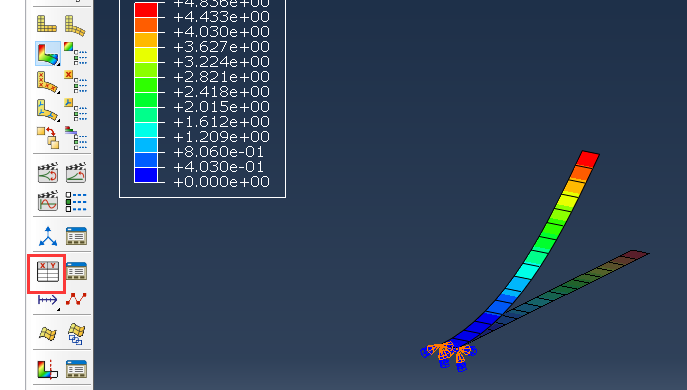
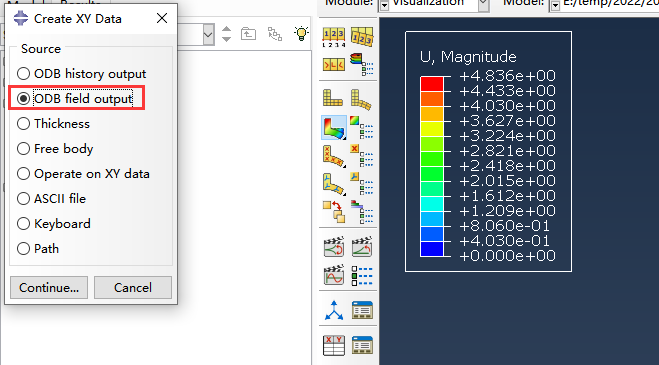
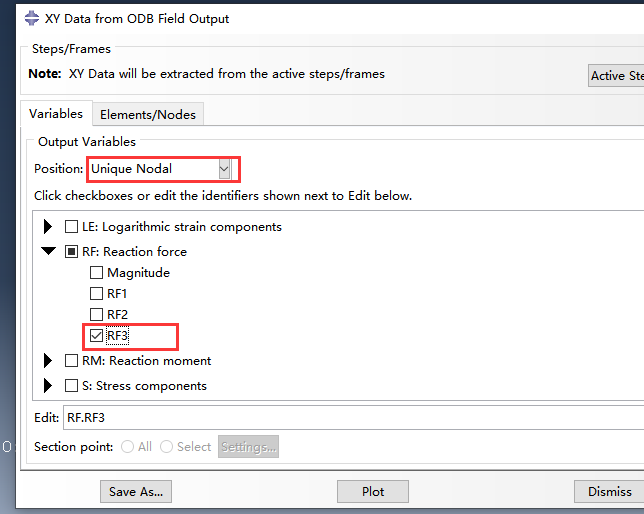
按上述选择后选择固定端节点，绘制节点的反力曲线。

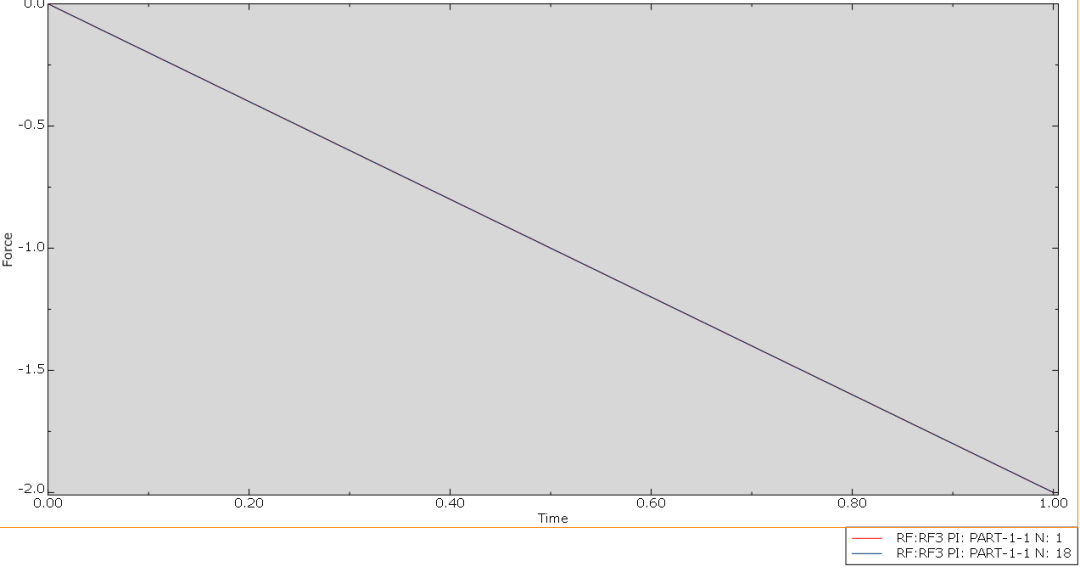
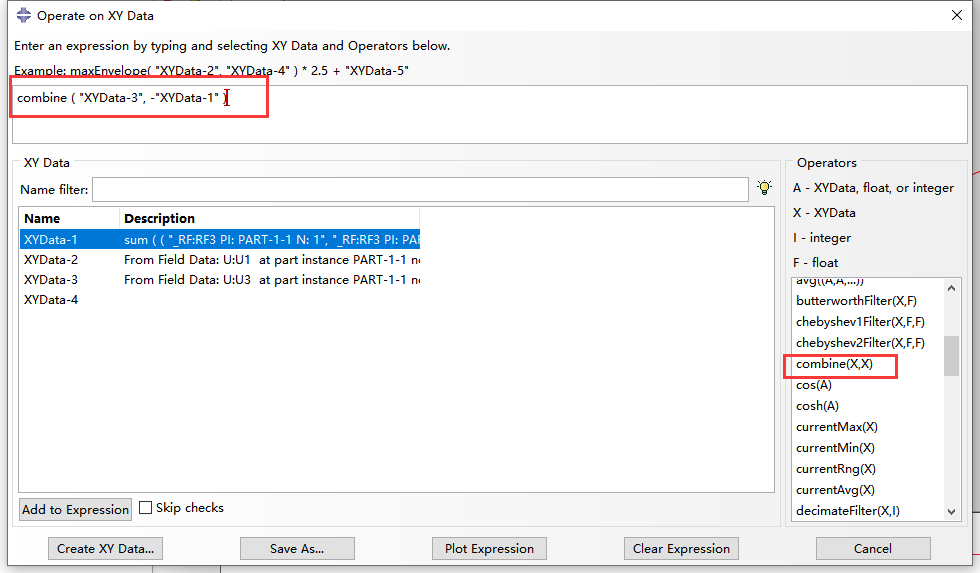
再对两个节点的反力采用xy plot edit求和：

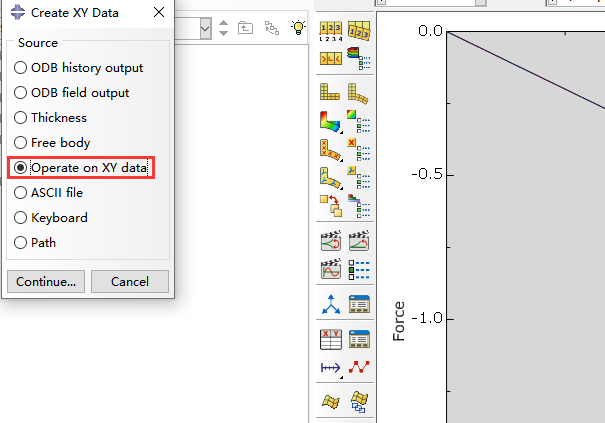
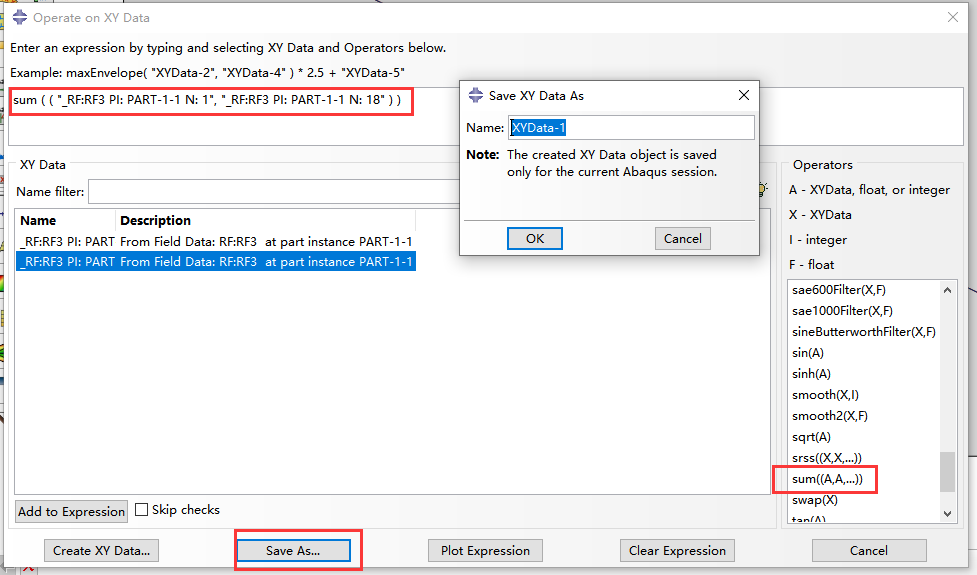
继续输出位移U1,U3，分别保存成xydata-2和xydata-3

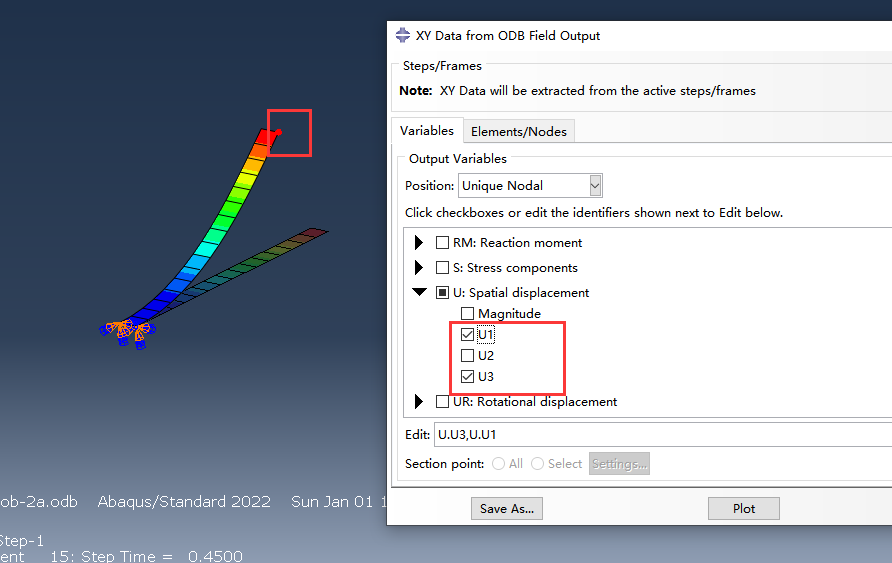
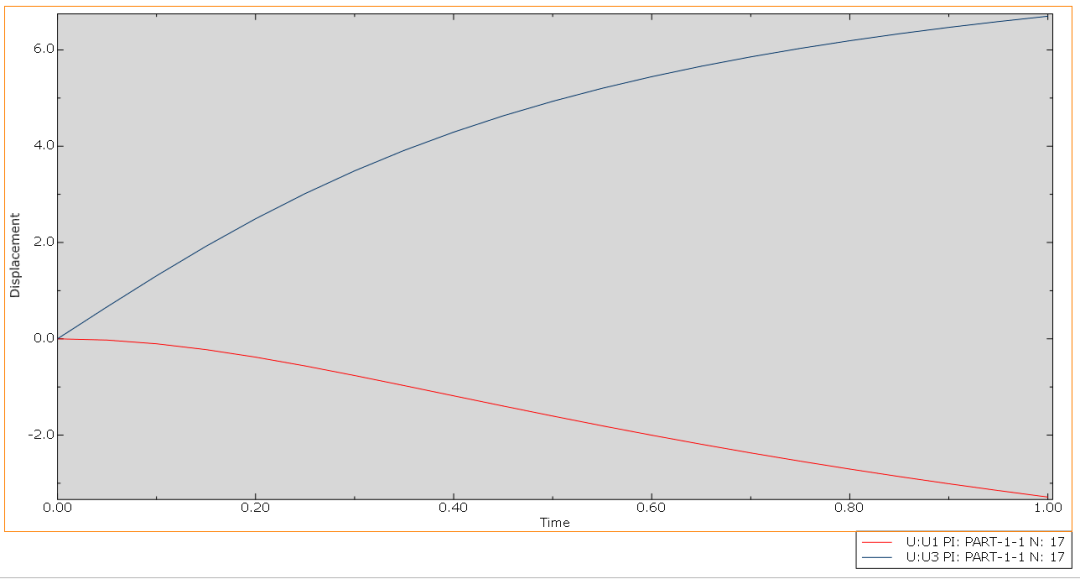
绘制荷载位移曲线

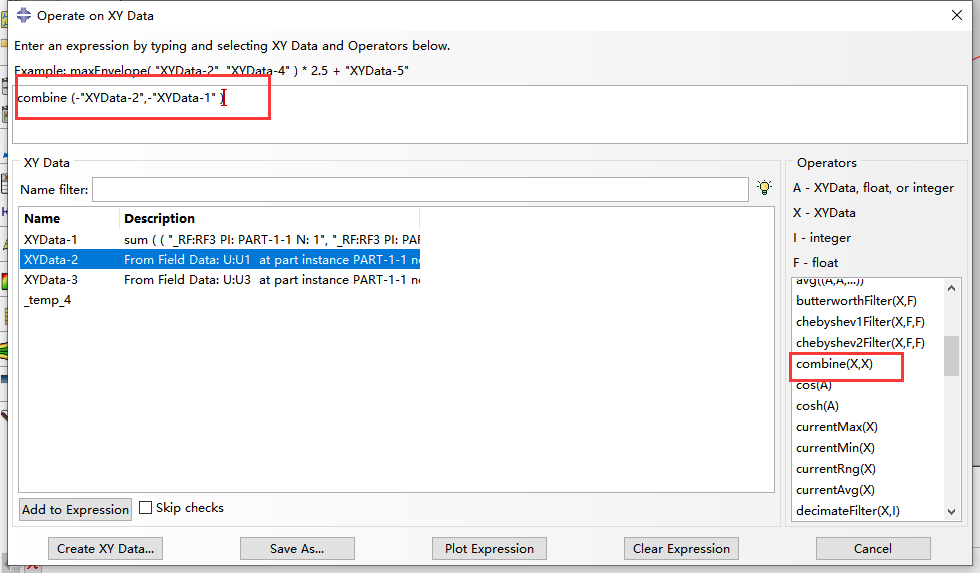
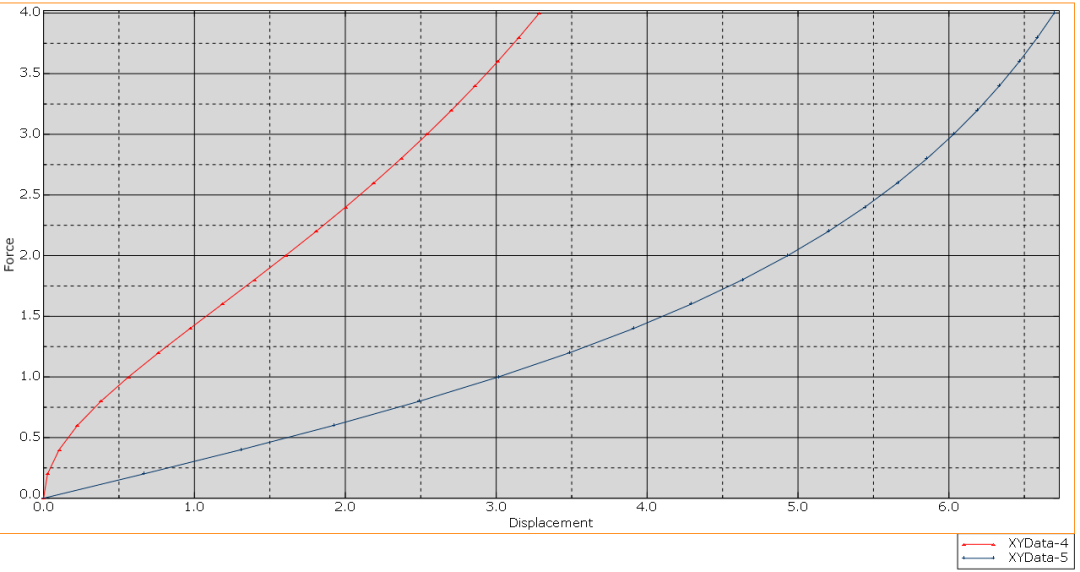
U1和U3向的具体最大位移数值：

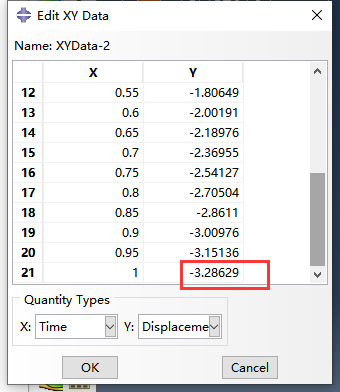
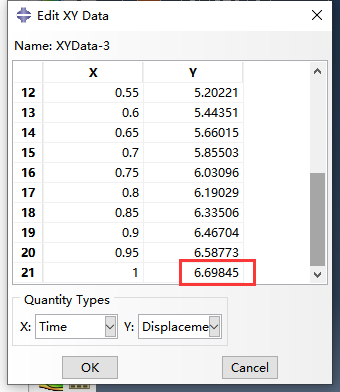
可见计算结果与文献中的结果基本一致。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删