ABAQUS中应用Prony系列实现线性粘弹性材料Maxwell模型

线性粘弹性材料广义Maxwell模型

粘弹性材料概括了材料的弹性和粘性特征，由弹簧和阻尼分别表征。广义Maxwell模型是多支Maxwell模型的组合。如图所示：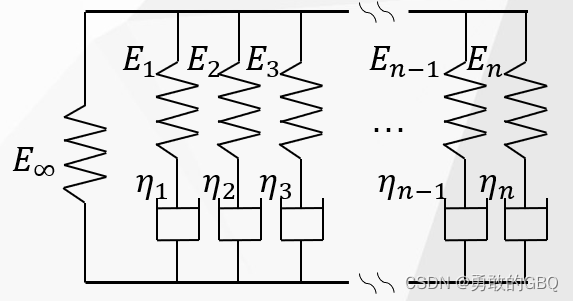

其在时域的数学表达式为：
E ( t ) = E ∞ + ∑ i = 1 N E i e − t / t R i (1) E(t)=E_infty+sum_{i=1}^{N} E_ie^{-t/t_{Ri}} ag{1} E(t)=E∞​+i=1∑N​Ei​e−t/tRi​(1)

   频域的数学表达式为：
E ( ω ) = E ∞ + ∑ i = 1 N E i ω t R i i 1 + ω t R i i (2) E(omega)=E_infty+sum_{i=1}^{N} frac{E_i omega t_{Ri}i}{1+omega t_{Ri}i} ag{2} E(ω)=E∞​+i=1∑N​1+ωtRi​iEi​ωtRi​i​(2)

   式中：
E ∞ — — E_infty —— E∞​——平衡模量；
E i — — E_i —— Ei​——第 i i i时刻的松弛强度
t R i — — t_{Ri} —— tRi​——第 i i i时刻的松弛时间， t R i = η i / E i t_{Ri}=eta_i/E_i tRi​=ηi​/Ei​
i — — i—— i——为虚数单位

Abaqus中的Prony 级数

引入 E 0 = E ∞ + ∑ i = 1 N E i E_0=E_infty +sum_{i=1}^{N} E_i E0​=E∞​+∑i=1N​Ei​，则 m i = E i / E 0 m_i=E_i/E_0 mi​=Ei​/E0​

   方程（1）可写做：
E ( t ) = E 0 ( 1 − ∑ i = 1 N m i ) + ∑ i = 1 N m i E 0 e − t / t R i (3) E(t)=E_0(1-sum_{i=1}^{N}m_i)+sum_{i=1}^{N}m_iE_0e^{-t/t_{Ri}} ag{3} E

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删