产品
橡胶材料的仿真分析通常都是选择超弹性本构模型,将材料特征假设为各方向同性、等温和弹性,在压缩载荷作用时完全或近似于不可压缩状态,从而实现材料的理想化。对于橡胶超弹体进行模拟仿真应该首要进行材料曲线的拟合工作,把实验数据转化成各种超弹模型能使用的应变能量密度函数系数,一般来说数据种类越多拟合出的曲线越能体现材料的真实属性。
橡胶类材料仿真中,常用的本构模型有Polynomial、Mooney-Rivlin、Ogden和Neo-Hookean几种,其中 Mooney-Rivlin模型受到广泛的应用,模型还分为N=2,3,5和9项,此时可看作是多项式形式的特殊情形。
2项Mooney Rivlin模型相当于N=1的多项式形式,是最常用的模式之一。
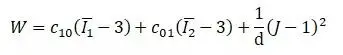
3项Mooney Rivlin模型与N=2且 C20=C02=0 的多项式形式类似。
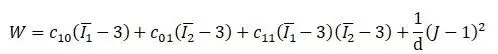
5项Mooney Rivlin模型相当于N=2多项式形式。
9项Mooney Rivlin模型相当于N=3的多项式形式。
所有的Mooney-Rivlin模型,初始体积模量和初始剪切模量是:
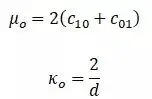
以上四种本构模型所具有的应用场景和特点基本可以概括为:
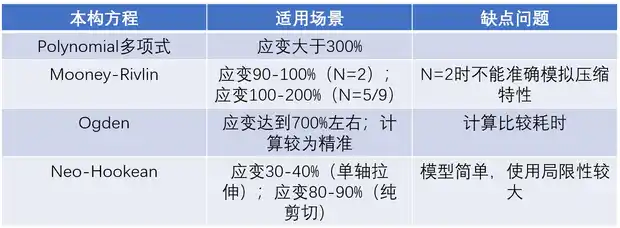
在对以上四种本构模型进行比较后,采用Polynomial多项式本构方程对橡胶材料的气球进行了定义,既可以很好的模拟300%以上应变情况,又可以加快仿真计算速度,制作了一个吹气球的仿真。
操作流程如图所示:
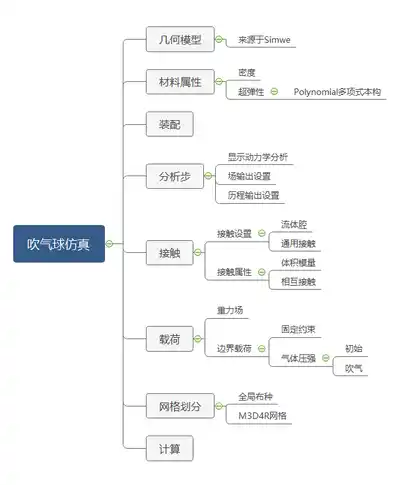
计算后,气球在压强的作用下逐渐变大。

免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删