在使用ANSYS 中经常会遇到两个零件的接触情况，ANSYS 中提供了五种接触算法，分别为罚函数法，一般拉格朗日法，增广拉格朗日法，多点约束法，梁约束法

如下图所示，在Mechanical 界面中进行接触设置时，默认的设置是Program Controlled，你可以根据自己的实际工况来选择更适合的接触算法

罚函数法Pure Penalty：

罚函数法是ANSYS 中的默认算法，适用于各类型的非线性接触(Frictional,Frictionless,Rough)，是相对于其他几种非线性算法中较为经济的一种算法

罚函数是将零件之间的接触假设成两个节点之间通过弹簧连接，通过以下计算公式来求解两个接触面之间的接触压力FNormal

FNormal=KNormal xpenetration

其中,

KNormal为两个接触面之间的接触刚度

xpenetration 为两个接触面之间的穿透量

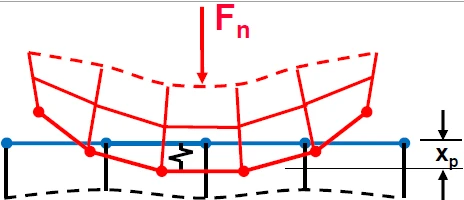
从上述公式可以看出，这种算法的精度较依赖于接触刚度和穿透量的大小。

在实际情况下，两个零件表面是不会有穿透的，这是一种为增强收敛性而进行的数值近似方法，因此，穿透量越小，计算结果精度越高，但同时收敛性较差

因此在使用罚函数算法的时候，需要仔细检查接触面的穿透量

一般拉格朗日Normal Lagrange

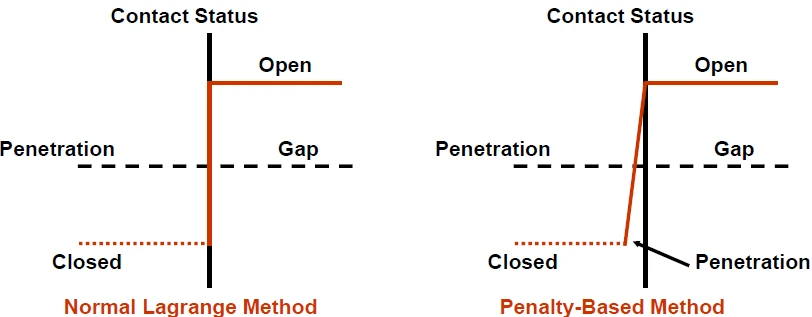
一般拉格朗日算法在将接触压力作为一个自由度来满足接触兼容性。因此它不需要计算接触刚度和穿透量来计算接触压力，而是将他看做一个自由度，于是，有如下两种情况：

1. 零件不接触
2. 零件接触

在计算过程中，这两种极限的情况会导致计算震荡剧烈从而较难收敛，但是一旦可以算收敛，由于这里没有假设零件之间的穿透，得到的结果精度较高。

另外，拉格朗日法需要使用直接求解器来求解，计算速度较慢

从下图可以看出，一般拉格朗日和罚函数在处理接触状态时的区别：

增广拉格朗日Augmented Lagrange

增广拉格朗日是在罚函数的方法上衍生出来的一种方法，他与罚函数法类似，但是在计算接触压力时，引入了附加项λ

FNormal=KNormal xpenetration+λ

引入了λ之后，可以看出接触压力对于接触刚度的敏感性降低，更利于在给定的接触刚度较大的时候收敛，可以一定程度上提高计算精度，但同时也会造成收敛时间加长

多点约束法MPC ：

多点约束法适用于绑定接触（Bonded），不分离(No seperation)。他在接触面间添加一个联结使两个面之间不出现分离。

若两个零件的几何模型间有缝隙，那么需要在计算结束之后仔细检查计算结果，以免出现计算出错

多点约束法适用于大变形开关开启的计算

梁约束法 Beam Contact:

梁约束法，顾名思义，就是在两个接触面之间添加无质量的梁进行联结，这种算法只适用于绑定接触（Bonded）

总结：

对于线性接触的两种计算方法，由于是线性计算，其收敛性都比较好，计算速度也较快。

对于三种非线性接触的计算方法，一般情况下，从计算精度和收敛性上的排序为：

• 收敛性：罚函数>增广拉格朗日>一般拉格朗日
• 精度：一般拉格朗日>增广拉格朗日=罚函数
• 计算时间：一般拉格朗日>增广拉格朗日>罚函数

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删