ANSYS CFD通用流体仿真基本工作流程（中部解析）

计算流体力学（Computational Fluid Dynamics简称CFD）是利用数值方法通过计算机求解描述流体运动的数学方程，揭示流体运动的物理规律，研究定常流体运动的空间物理特性和非定常流体运动的时空物理特征的学科。

其基本思想可以归纳为：把原来在时间域和空间域上连续的物理量的场，如速度场和压力场，用一系列有限个离散点上的变量值的集合来代替，通过一定的原则和方式建立起关十这些离散点上场变量之间的关系的代数方程组，然后求解代数方程组获得场变量的近似值。

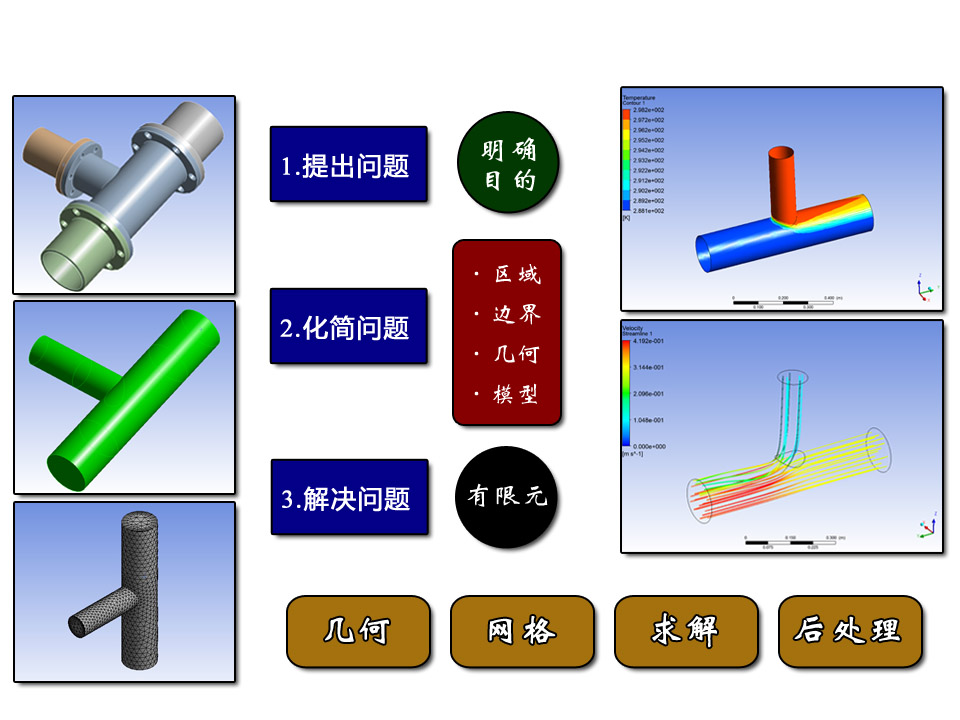
ANSYS CFD 的基本工作流程可以认为分成三个主要的部分：

★ 提出问题

★ 化简问题

★ 解决问题

（二）化简问题

有了明确的仿真目的，我们接下来的任务就是化简问题。当然，仿真的问题该如何围绕这明确的目的进行化简，这些工作（思考）通常也应该是在仿真之前就完成的。对于问题的简化，大致上可以分为以下四个方面：

★

  仿真区域选取

★

  边界条件给定

★

  几何模型化简

★ 物理模型选择

1.仿真区域选取

在流体力学中的守恒方程中，通常大家第一个讨论的就是连续性方程，这个方程从某种意义上来讲，也可以认为是流体区别于固体（就是我们常说的结构仿真）的主要区别。农夫山泉有一句著名的广告词叫“我们不生产水，我们是大自然的搬运工”也是很形象的说明了流体力学中连续性方程的含义：对于一个给定的观测体（仿真区域）流体不会凭空的生成和消失，流体流入多少就会对应的流出多少；同时，流体流出观测体（仿真区域）后也不会消失，而是继续的流动，一直到无穷远的地方（或循环）。

因此，对于流体永久存在（循环）的流体区域，取其中一部分进行仿真分析，本身也是对问题的一个简化。当然，仿真的区域如何选取，不同的情况应该如何应对，由于篇幅的关系，本文就不做详细介绍了。

对于三通管的问题，我们选取了接头的部分作为仿真区域，当然，这并不代表流体从三通管接头直接流到大气之中，而是表示在出口的位置，还有等径圆直管在无限延伸，流体从出口的位置流进了这无限长的直管中。

2. 边界条件给定

边界条件给定和选取的仿真区域息息相关，因此也是简化问题的重要步骤。从本质上理解，边界（面）实际上是一种等效，仿真中用它们来替代其他的流体区域。

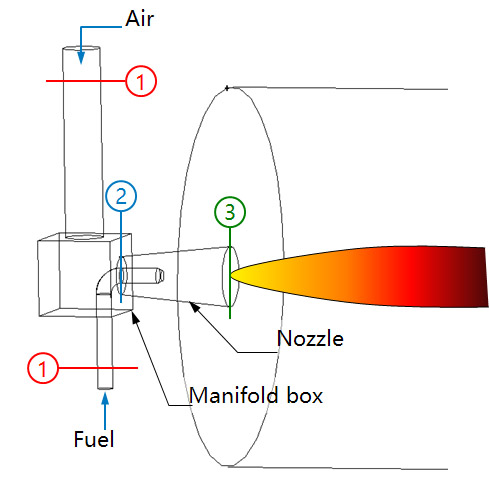
不同的计算区域选取对应着不同的边界条件给定，如下图所示：

★

  如果选取①作为入口，那么只需要简答的输入即可，缺点是计算区域会很大

★

  如果选取②③作为入口，那么虽然计算区域相对会缩小，但是给定的边界条件需要精确的分布，当然，这些分布在①中是可以直接计算的得到的。

3.几何模型化简

如果在流体问题中考虑过于精细的几何细节（如螺栓形状、小凹槽等）那么会使网格量成指数增加，导致工作效率降低。因此我们必须要非常清楚哪些几何细节是对我们的仿真有影响的；没有影响的，一律简化，这样也是工程中效率优先思想的一个重要体现。

4.物理模型选择

仿真中的物理模型，可以简单理解为用方程来代替实际的物理现象：如湍流模型、多相流模型、热辐射模型等，无论何种模型，都是抓住了主要矛盾、简化了次要矛盾才诞生的。因此可以这样说，模型本身就是简化的代名词。流体中的这些问题（湍流、多相流），如果不用模型，任何一个都无法完成计算。

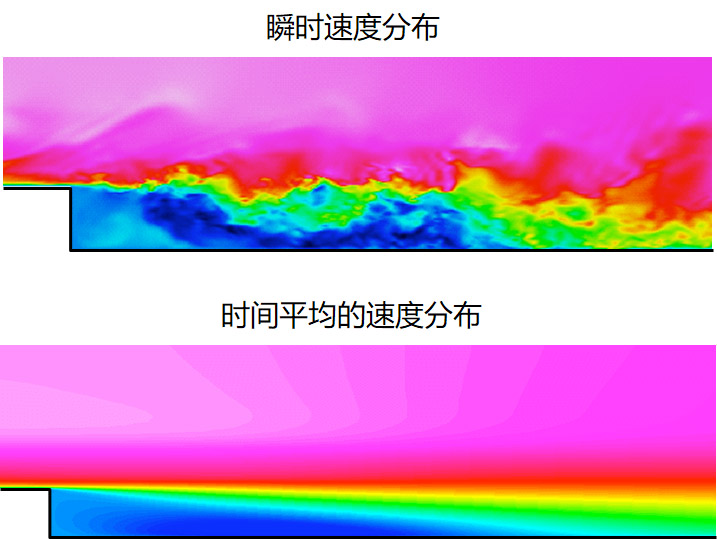
当然，在明确的仿真目的下选择必要的物理模型也是可以简化问题的，如：

★

  某液体的流动，只关注速度与压力的影响（不需要开启传热模型）

★

  某颗粒流中颗粒体积分数很小，颗粒对流场影响可以忽略（不需要开启DPM与流场耦合计算，仅做流场后处理即可）

★

  某真空环境下换热问题（不需要开启流动方程计算，仅计算能量方程和辐射输运方程即可）

★

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删