Abaqus阻尼定义全解

非线性问题直接积分求解(显式分析或者隐式分析)；直接法或子空间法稳态动力学分析；模态动力学分析(线性)。

针对模态动力学分析，在ABAQUS/Standard中可定义几种不同类型的阻尼：直接模态阻尼(Direct Modal Damping)，瑞利阻尼(Rayleigh Damping)，复合模态阻尼(Composite Modal Damping)和结构阻尼(Structure Damping)。

ABAQUS模态动力学分析中用*MODAL DAMPING选项来定义阻尼。阻尼是包含在分析步内定义的一部分，每阶模态可以定义不同量值的阻尼。

1、直接模态阻尼

采用直接模态阻尼可以定义对应于每阶模态的阻尼比ξ。其典型的取值范围是在临界阻尼的1％～10％之间。直接模态阻尼允许用户精确定义系统的每阶模态的阻尼。

在分析步骤内定义直接模态阻尼。如图1所示，激活直接模态阻尼选项(Direct modal)，并在数据行内输入数据

对应的ABAQUS输入文件为：

*MODAL DAMPING, MODAL=DIRECTm1, m2, ξa

其中，*MODAL DAMPING选项中的MODAL=DIRECT 参数表示被指定的直接模态阻尼，数据行输入的数据m

1为起始模态序号，

m2为截止模态序号，　　

ξa为模态阻尼比。

例如，对于前10阶振型的阻尼定义为4%的临界模态阻尼，11～20阶振型的阻尼为5%的临界阻尼，在分析步骤中的定义如下：

*MODAL DAMPING, MODAL=DIRECT1，10，0.04  11，20，0.05

2、瑞利阻尼

在瑞利阻尼中，假设阻尼矩阵可表示为质量矩阵和刚度矩阵的线性组合，即C=αM +βK (1)其中，α和β

是用户根据材料特性定义的常数。尽管假设阻尼正比于质量和刚度没有严格的物理基础，但是实际上我们对于阻尼分布的真实情况知之甚少，也就不能保证其它更为复杂的模型是正确的。通常，瑞利阻尼模型对于大阻尼系统，即阻尼值超过10%临界阻尼时是不可靠的。

使用瑞利阻尼有许多方便，例如系统的特征频率与对应的无阻尼系统特征值一致；相对于其它形式的阻尼，可以精确地定义系统每阶模态的瑞利阻尼；各阶模态的瑞利阻尼可转换为直接模态阻尼，在ABAQUS/Standard中将瑞利阻尼转换为直接模态阻尼进行动力学计算。

对于一个给定模态i，临界阻尼值为ξi，而瑞利阻尼系数α和β的关系为：

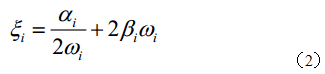
其中ωi表示第i阶模态的固有频率。

(2)式表明，瑞利阻尼的质量比例阻尼部分在系统响应的低频段起主导作用，刚度比例阻尼部分在高频段起主导作用。

ABAQUS在模态动力学分析步骤内定义瑞利阻尼。如图2所示，激活瑞利阻尼选项(Reyleigh)，并输入数据。如果需要定义多阶模态的阻尼值，则可在菜单内点击鼠标右键，通过insert row before或者insert row after来增加数据行。

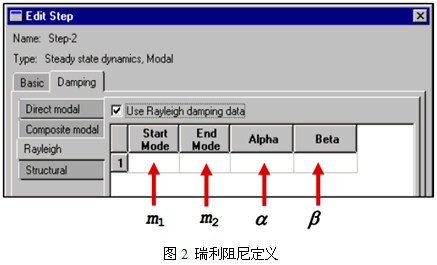
对应的ABAQUS文件输入为：

*MODAL DAMPING, RAYLEIGH

m1, m2, α，β

参数

RAYLEIGH

指定阻尼形式为瑞利阻尼，m1、m2的含义与直接模态阻尼定义相同。

α、β分别为模态质量、刚度比例系数。

例如，对前10阶模态定义α=0.2525 和β=2.9×10−3，对于11～20阶振型定义α= 0.2727和β=3.03×10−3，则可以在分析步骤中定义：

*MODAL DAMPING, RAYLEIGH1,10,0.2525,2.9E-311,20,0.2727,3.03E-3

3、复合阻尼

在复合阻尼中，对应于每种材料的阻尼定义一个临界阻尼比，这样就得到了对应于整体结构的复合阻尼值。如果结构由多种材料组成，那么采用复合阻尼来描述系统的阻尼特性是非常简便有效的。

ABAQUS将材料的复合阻尼加权平均得到模态阻尼比，转换关系为：

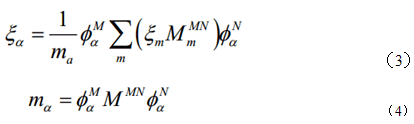
其中，ξa为模态α的模态阻尼比，ξm材料m的阻尼比， MmM N为与材料m相关的质量矩阵， φαM为模态α的振型， ma为模态的α模态质量。

在ABAQUS中分两步定义复合阻尼。

第一步，在材料属性中定义与该材料对应的复合阻尼，如图3所示。

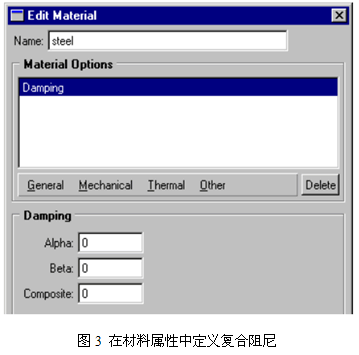
对应的ABAQUS输入文件为：

*MATERIAL, NAME=STEEL

*DAMPING, COMPOSITE=ξM

其中ξM为材料“STEEL”的临界阻尼比。

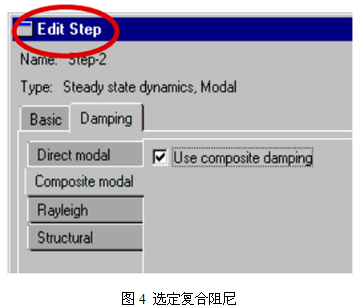
然后在分析步骤中引用复合阻尼，如图4所示。

对应的ABAQUS文件输入为：

*STEP

……

*MODAL DAMPING, MODAL=COMPOSITE

4、结构阻尼

系统的结构阻尼特性与结构或者材料的内摩擦机理有关。其他形式的阻尼属于粘性阻尼，即阻尼力的大小与运动速度成正比，而结构阻尼力与位移成正比。同时结构阻尼力不会随着激振频率变化而变化。

结构阻尼力可用下式来表示：

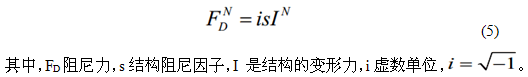
结构阻尼力的方向与速度方向相反，与其位移相比滞后90°。只有当位移和速度的相位差为90°时，结构阻尼假设才能成立，因此激励必须是正弦函数。

使用结构阻尼假设的动力学分析包括稳态响应分析和随机响应分析，其他如瞬态动力学分析则不能直接应用结构阻尼；对于某些问题如果只能得到结构阻尼，那么必须依据一定的准则将结构阻尼转换为等效的粘性阻尼。

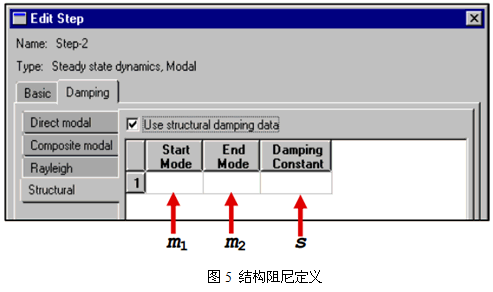
图5为结构阻尼定义菜单。

对应ABAQUS输入文件为：

*MODAL DAMPING, STRUCTURALm1, m2, s

参数

STRUCTURAL

指定模态阻尼形式为结构阻尼。

m1、m2的含义与定义直接模态阻尼相同，s为结构阻尼因子。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删