圆拱曲线弯曲特性的深入分析

通常有必要研究其部分装载历史期间其响应不稳定的结构的后屈曲行为。本例中的两个模型说明了使用修改后的Riks方法，该方法用于处理这种情况。该方法基于在由位移和比例加载参数限定的空间中沿着静态平衡路径以固定增量移动。实际负载值随着解决方案的进行而增加或减少。 Abaqus理论指南“2.3.2节的”修改的Riks算法“中描述了在Abaqus中实现的修改后的Riks方法。

其他两个模型说明了使用粘滞阻尼。一个实例应用粘性阻尼作为表面接触的特征，其允许定义与表面之间的相对速度成比例的“粘性”压力。 “Abaqus理论指南”第5.2.1节“接触压力定义”中描述了Abaqus中此选项的实现。另一个例子将体积比例阻尼应用于模型。 “Abaqus Analysis用户指南”第7.1.1节“解决非线性问题”的自动稳定部分介绍了该选项的实现。

这里考虑了三种不同的情况。第一个是经受压力负载的夹紧的浅拱。这种情况的参考解决方案由Ramm（1981）和Sharafi和Popov（1971）给出。第二种情况是经受点载荷的夹紧铰链圆弧的不稳定性分析。 DaDeppo和Schmidt（1975）给出了该问题的确切解决方案。第三种情况是浅拱问题的修改，其中端部被钉扎而不是被夹紧，并且拱被刚性冲头压下。

模型和解决方案控制

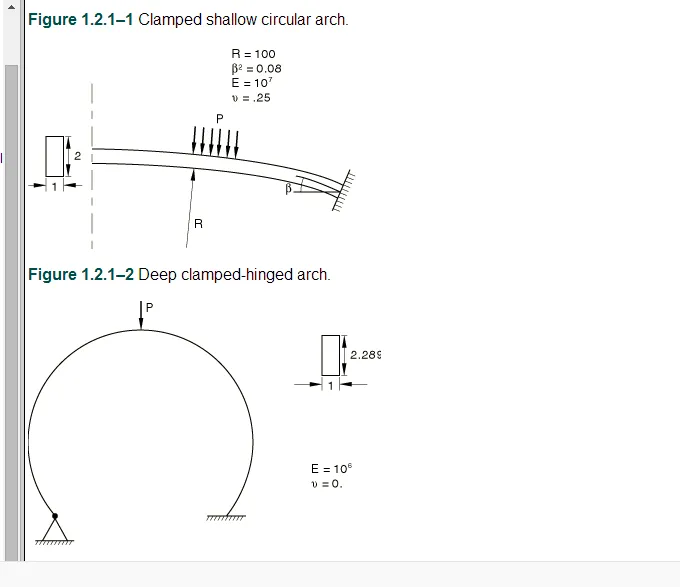
浅圆拱如图1.2.1-1所示。由于变形是对称的，拱的一半被建模。使用B21型（线性插补光束）的10个元件。首先施加均匀的压力以将弓穿过。然后将负载反向，以便在压力被去除时也发现行为。

深圆弧如图1.2.1-2所示。拱的一端被夹紧，另一端铰接。在拱顶部施加集中的载荷。弓经历极大的偏转，但小的应变。由于不对称边界条件，拱门将向铰链端移动，然后塌陷。对于大多数的响应历史来说，这个拱门几乎是不可分割的。使用类型B31H的六十个元素。使用混合元素，因为它们最适合于诸如此类的问题。

解决方案控件用于设置非常紧的收敛容限，因为问题包含多个平衡路径。如果不使用严格的公差，则响应可能遵循与所示路径不同的路径。

在Riks程序中，不能指定负载大小的实际值。相反，它们作为解决方案的一部分计算，因为“负载比例因子”乘以加载数据线上给出的负载大小。用户规定的负载大小仅用于定义方向并估计步长的负载初始增量的大小。该初始负载增量是初始时间增量与时间段的比率以及加载选项中给出的负载量值的乘积。用户可以通过指定最大负载比例因子或节点处的最大位移或两者来终止Riks分析。当计算出这些限制中的任何一个的解点时，分析将停止。无论如何，或者如果两个选项都不被使用，分析结束时超出步长的最大增量。

在诸如这些的直通式研究中，结构可以在完全捕捉之后承载增加的负载。因此，通过指定最大负载比例因子便于方便地进行分析。

对于夹紧的浅拱，初始咬合发生在约-1000（力/长度2单位）的压力下。因此，-250（力/长度2单位）似乎是要应用的负载的第一增量的合理估计。因此，在1.0的时间段和-5000的压力负荷（力/长度2单位）中规定了初始时间增量为0.05。该解决方案将在约-2000（力/长度2单位）的压力下充分发展。因此，当负载比例系数超过0.4时，分析结束。

为了说明在几个步骤中使用Riks，还包括第二步，其中将压力从拱顶上取下，使其将朝向其初始配置。在Riks分析中的任何一点，实际负载由下式给出： p0在前一步骤结束时的负载 是当前步骤中规定的负载大小，并且 是负载比例系数。拱被卸载，使得在初始时间增量中，去除约0.15 的压力。在1.0的时间段内使用0.05的初始时间增量，对该重新启动的步骤规定了负载。此外，我们希望分析结束时，所有的负载被删除，并且拱已经返回到其初始配置。因此，为拱的中心设定位移阈值0.0。当这个限制被越过时，分析结束。因为Abaqus必须在初始Riks步骤结束时接收负载大小以启动下一步，所以Riks步骤之后的任何步骤只能作为上一步骤中的重新启动作业完成。

对于深度夹紧铰链，初始卡扣发生在约900（载荷单位）的载荷下。指定的负载大小为100（力单位），最大负载比例系数指定为9.5。

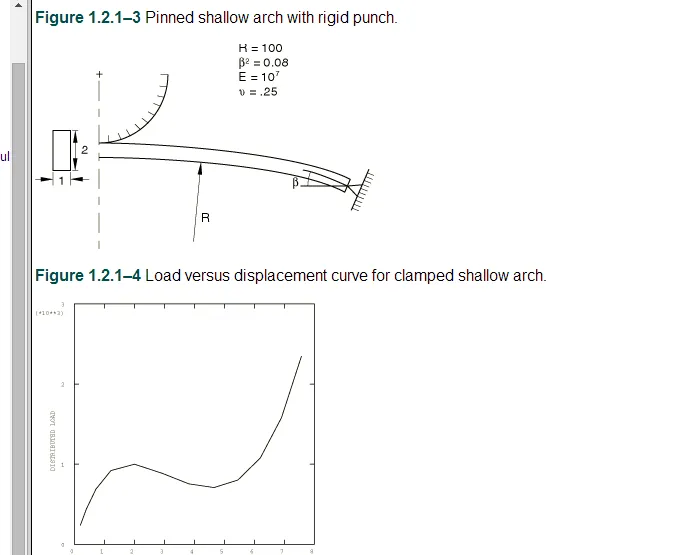
用刚性冲头压下的浅拱形如图1.2.1-3所示。分析使用与第一个问题相同的拱形模型。然而，端部被固定而不是夹紧，并且通过冲头的位移施加负载。固定边界条件使得问题比夹紧端的情况更不稳定。一个初步的分析，其中弓被拱形中点的指定位移压下，表明该力在卡通过程中将变为负值。因此，如果拱形物用刚性冲头压下，则Riks方法将不会帮助收敛，因为在弯曲的瞬间，拱与冲头分离，并且冲头的移动不再控制拱的位移。因此，引入接触阻尼以帮助收敛。具有表面接触的粘性阻尼增加了与相对速度成比例的压力，以减慢拱与冲头的分离。

粘滞阻尼间隙设定为10.0，间隙间隔的分数设定为0.9;对于高达9.0的间隙，阻尼是恒定的。由于拱顶高度为4.0，所以拱顶从初始位置到最终卡通位置的距离为8.0单位。在分析期间的任何时间，这个距离明显大于拱的中间和冲头的间隙。因此，当拱形件与冲头分离时，粘滞阻尼在整个时期都有效。

要选择粘性阻尼系数，请注意以相对速度的压力给出。通过将近似峰值力（10000.0）除以接触面积（1.0）获得相关压力。相关速度通过将弓的顶部行进的距离（从起始到捕捉位置8.0（可以舍入到10.0））除以时间（大约1.0，步长的总时间）来获得。该值的一小部分（0.1％）用于粘滞阻尼系数：

使用1.0，分析完成。进行另一个分析，其值较小，值为0.1，但是粘滞阻尼不足以使分析能够通过跳跃点。因此，1.0的阻尼系数被确定为适当的值。

对于用刚性冲头压缩的浅拱也考虑了基于体积比例阻尼的自动稳定，作为接触阻尼的替代。考虑到两种形式的自动稳定：一种具有恒定阻尼因子，默认情况下选择（参见“解决非线性问题时，使用恒定阻尼因子自动稳定静态问题”，“Abaqus分析用户指南”第7.1.1节），一个具有自适应阻尼因子（参见“解决非线性问题”中的“自适应自动稳定方案”，“Abaqus分析用户指南”第7.1.1节）。

结果与讨论

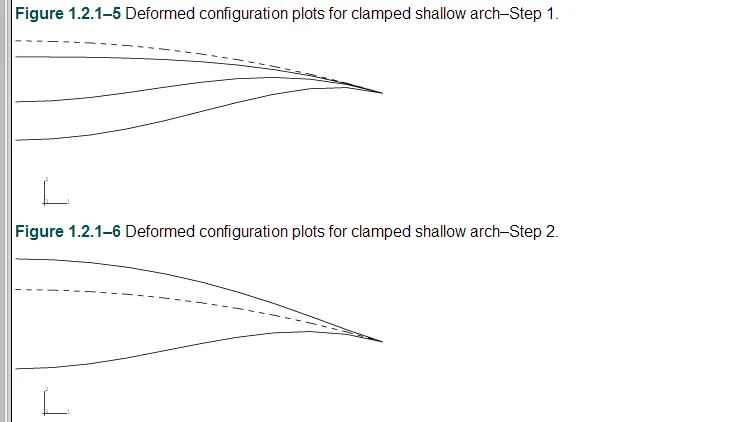
夹紧浅拱的结果如图1.2.1-4所示，其中拱顶的向下位移作为压力的函数作图。该算法以12个增量获得该解，最大值为3次迭代。在12增量结束时，拱顶的位移约为7.5个长度单位。这代表了一个完整的通过，因为拱的原始上升是4个长度单位。图1.2.1-5和图1.2.1-6显示了这个问题的一系列变形配置图。其他一些作者已经研究了同样的情况，并获得了基本相同的解决方案（参见Ramm，1981，Sharafi和Popov，1971）。

深夹紧铰链的结果如图1.2.1-7所示，其中拱顶的位移作为施加载荷的函数作图。图1.2.1-8显示了这个问题的一系列变形配置图。拱顶在峰值载荷下不稳定地折叠。此后，当负载增加时，梁会迅速变硬。这个例子很好地说明了Riks方法处理不稳定响应的能力。

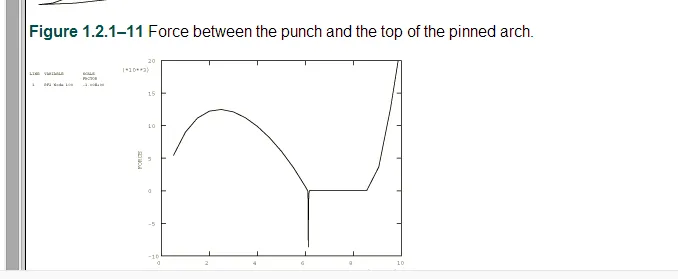
钉扎浅拱的规定位移的初步分析结果如图1.2.1-9所示，拱顶部的位移作为该点反作用力的函数。此图显示了快速通过期间产生的负力。图1-2.1-10给出了用冲头和粘性阻尼引入的钉扎浅拱的一系列变形配置图，其中一个曲线显示了与冲头分离的拱。图1.2.1-11是冲头和拱顶之间的力的曲线图。当拱形件与冲头分离并产生负的粘性力时，力是正直的。一旦卡通完成，当冲头与拱门分离时，冲头继续向下移动，力将下降到零。当冲头接触拱门时，会再次产生积极的力量。

当接触粘性阻尼由体积比例阻尼（具有常数或自适应阻尼系数）代替时，产生类似的结果。获得了如图1.2.1-10所示的一系列配置，其中在卡通过程中发生弓与冲头的分离。在分析结束时，耗散的能量量与粘性阻尼选项消耗的量相似。

可以使用abaqus restartjoin执行过程从重新启动分析创建的输出数据库中提取数据，并将数据附加到第二个输出数据库。有关更多信息，请参阅“从重新启动的分析中加入输出数据库（.odb）”文件，“Abaqus Analysis用户指南”的第3.2.21节。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删