Abaqus中非线性屈曲分析的高效方法

在Abaqus中，对于屈曲的计算考虑则依据结构的复杂性而定，简单的可以只考虑线性屈曲分析预估临界载荷大小；对于较复杂的模型，则可以考虑Riks 法进行后屈曲计算，从而可获取屈曲以后的结构响应情况；但对于涉及接触脱开等特别复杂的问题，可能得借助Explicit 来实现；而对于局部褶皱问题需要借助Static、Stabilize来实现。

01

线性屈曲分析

线性屈曲分析用于预估临界失稳载荷和失稳模态，所求得的屈曲特征值与所加载的载荷大小相乘就是临界失稳载荷。当然，对完善结构的屈曲问题，线性屈曲分析也为后屈曲分析引入缺陷（扰动）做好准备，这是非常关键的。

在Abaqus中，进行线性屈曲分析的方法是通过Buckle 进行的。

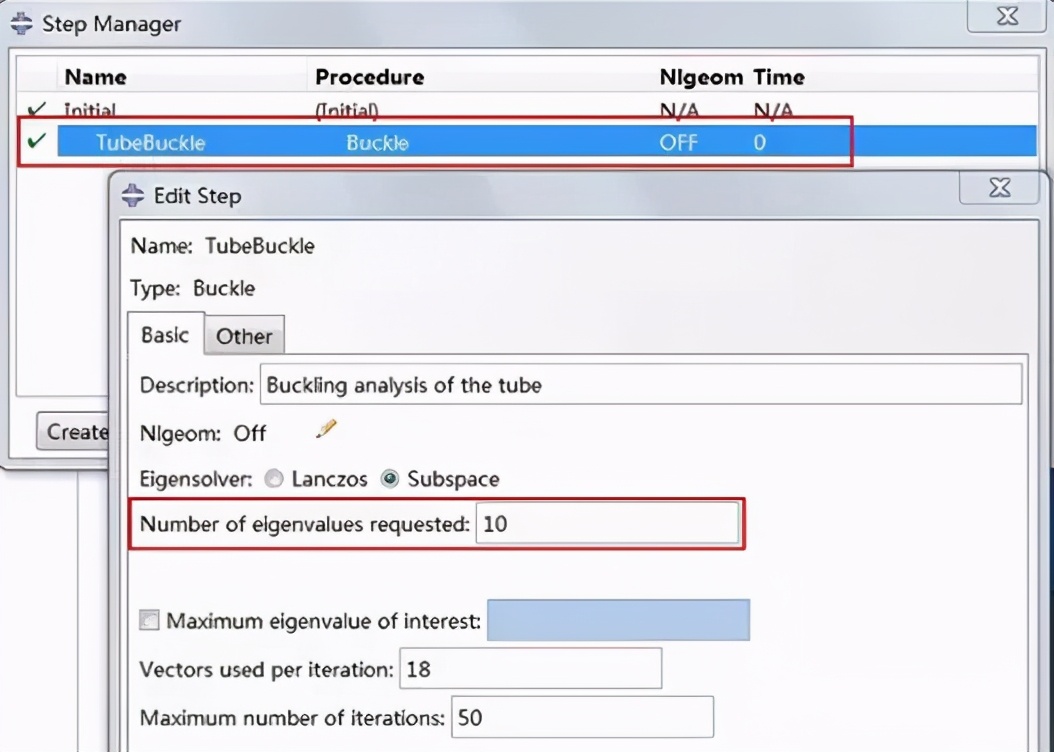
一般线性屈曲分析只需要关注第一阶屈曲模态，并根据计算所得的第一阶屈曲载荷因子预估使结构发生屈曲所需要的临界载荷是多大。但通常而言，线性屈曲分析得到的临界失稳载荷大小是保守的，偏大的。为了获取更加准确的结果，特别是复杂模型，就需要进行非线性屈曲分析（或称为后屈曲分析）。

因此，通常会在线性屈曲分析中考虑添加关键字作为后屈曲分析的扰动引入参数。具体做法如下（注意关键字的插入位置和书写格式）：

再提交计算后，会生成相应的.fil 文件，该.fil 文件将在后屈曲分析中进行引用！

02

后屈曲分析

后屈曲分析通常在线性屈曲分析后，通常的做法是将原线性屈曲模型复制生成新的模型，并调整和修改分析步和载荷工况、接触等。比如方筒的压溃，就需要修改为显示动力学分析，添加自接触关系等。当然最重要的是要引入缺陷扰动，即调用之前生成的.fil 文件。具体做法如下：

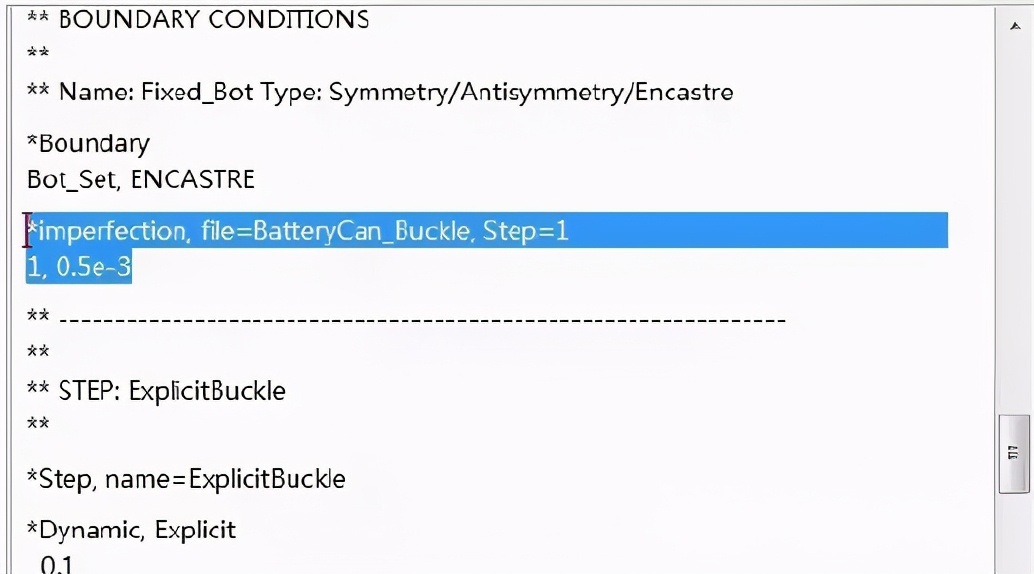
其中，关键字中file 后面的名称即调用的前面的.fil 文件的名称，第二行第一个数字1表示引入的是第一阶线性屈曲的扰动结果，0.5e-3表示引入的扰动量的大小。

扰动量（或称为缺陷因子）的大小准确的做法是进行试验矫正，一般是按照经验的做法，取壳厚或杆长的1‰~2‰。

实际上，在一定程度上你也可以调整扰动量的大小进行试算并比对后屈曲状态和其他计算结果参数，如果结果变化不大，说明结构对缺陷的敏感性较低，反之表示相对敏感。当然，这个观点还有待深入考究。

GIF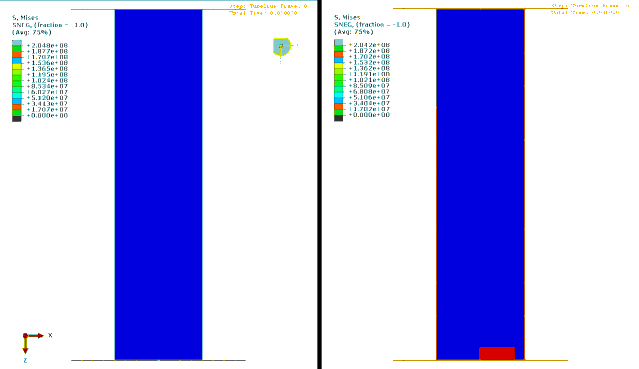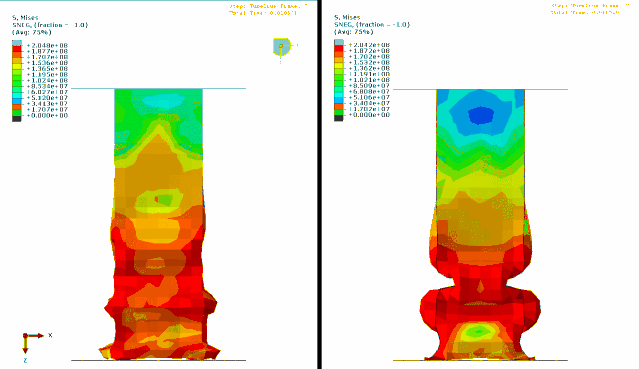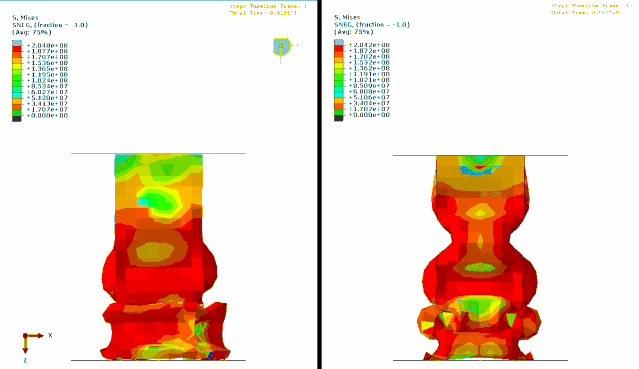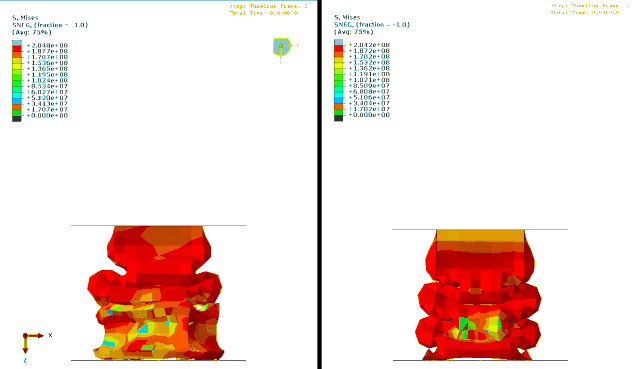

上图中左图没有考虑引入扰动量，右图是考虑扰动量的结果。大家可以仔细观察下结果的区别。

实际上右图在压溃的过程中，相对光滑，结果相对更加合理。

当然，对于方筒这类实际上是通过显示方法实现的，更准确的讲是动力屈曲分析，所以我们还得判断动能、塑形耗散等能量参数，才能使结果更加准确。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删