由于玻璃钢复合材料的薄壁圆筒结构具有强度高、重量轻、刚度大、耐腐蚀, 电绝缘及透微波等优点,目前已广泛应用于航空航天和民用领域中。工程中广泛 使用的这些薄壁圆筒,当它们受压缩、剪切、弯曲和扭转等荷载作用时,最常见 的失效模式为屈曲。因此,为了保证结构的安全,需要进行屈曲分析。
对结构进行屈曲分析,涉及到较复杂的弹(塑)性理论和数学计算,要通过求 解高阶偏微分方程组,才能求解失稳临界荷载,而且只有少数简单结构才能求得 精确的解析解。因此,只能采用能量法、数值方法和有限元方法等近似的分析方 法进行分析。近 20 年来,随着计算机和有限元方法的迅猛发展,形成了许多的 实用分析程序,提高了对复杂结构进行屈曲分析的能力和设计水平。ABAQUS 就是其中的杰出代表。
1.屈曲有限元理论
有限元方法中,对结构的屈曲失稳问题的分析方法主要有两类:一类是通过 特征值分析计算屈曲载荷,另一类是利用结合 Newton—Raphson 迭代的弧长法 来确定加载方向,追踪失稳路径的几何非线性分析方法,能有效分析高度非线性 屈曲和后屈曲问题。
1.1 线性屈曲
假设结构受到的外载荷模式为P0。幅值大小为λ,结构内力为Q,则静力平 衡方程应为λP0= λQ
进一步考察结构在(λ+△λ)P0载荷作用下的平衡方程,得到{[KE] + [KS(S+λ△S)] + [KG(ũ+λũ)]}△ũ =△λP0 由于结构达到保持稳定的临界载荷时有△λ,代入上式得该方程对应的特征值问题为det{[KE]+λ[KS△σ]+KG(△ũ)}=0
如果忽略几何刚度增量的影响,屈曲分析的方程又可进一步简化为
det{[KE] + λ[KS △ σ]} = 0
该方程即为求解线性屈曲的特征值方程。λ为屈曲失稳载荷因子,(△ũ)为结 构失稳形态的特征向量。
1.2 非线性屈曲
非线性屈曲分析方法多采用弧长法进行分步迭代计算,在增量非线性有限元 分析中,沿着平衡路径迭代位移增量的大小(也叫弧长)和方向,确定载荷增量的 自动加载方案,可用于高度非线性的屈曲失稳问题。与提取特征值的线性屈曲分 析相比,弧长法不仅考虑刚度奇异的失稳点附近的平衡,而且通过追踪整个失稳 过程中实际的载荷、位移关系,获得结构失稳前后的全部信息,适合于高度非线 性的屈曲失稳问题。
2.ABAQUS 的线性屈曲分析
ABAQUS 中提供两种分析方法来确定结构的临界荷载和结构发生屈曲响应 的特征形状:线性屈曲分析(特征值屈曲分析)、非线性屈曲分析。
线性屈曲分析用于预测一个理想的弹性结构的理论屈曲强度。它是预期的线 性屈曲荷载的上限,可以作为非线性屈曲分析的给定荷载,在渐进加载达到此荷 载前,非线性求解必然发散;它还可以作为施加初始缺陷或扰动荷载的依据。所 以预先进行特征值屈曲分析有助于非线性屈曲分析,进行特征值屈曲分析是必要 的。
3.算例
3.1 问题概述
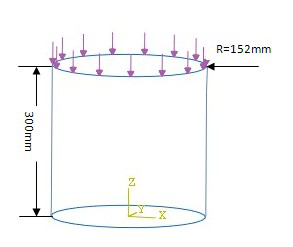
图 3-1 实例模型
如图所示两端开口的复合材料薄壁圆筒,底端固支,顶端作用有均匀分布的 轴压边载。半径 R=152mm,高度 300mm,厚度 t=0.804mm,对称铺层[±45,0]s,单层厚度为 0.134mm。复合材料圆筒的材料参数如下表:
表 1 AS4/3501-6 石墨/环氧的弹性参数
| 弹性模量 | 参数 |
| E1/GPa | 142 |
| E2/GPa | 9.7 |
| G12/GPa | 6 |
| G13/GPa | 3.6 |
| G13/GPa | 3.6 |
| μ | 0.3 |
3.2 建模、划分网格及分析过程
3.2.1 ABAQUS 进行前处理建立模型
首先先绘制一个半径为 152mm 的三维轮廓图,然后进行拉伸 300mm 创建 一个具有平面壳体单元的三维变形体。
其次进入 property 模块生成材料,参考上表编辑其弹性参数。编辑截面进行 复合层板的铺层完成材料属性、截面属性的定义。
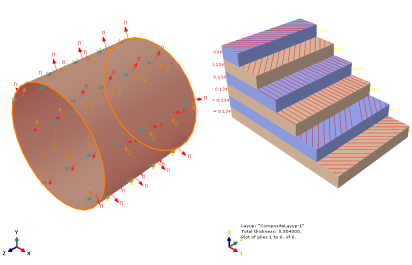
图 3-2 铺层
接着生成装配件,定义屈曲分析步。对所建模型施加边界条件和施加载荷。将圆筒的一端固支,另一端施加单位 1 的均布轴边压载。
最后进行网格划分。考虑到在复合材料层合壳模型中剪切柔度的影响,可采 用厚壳单元 S4R 来模拟它。所得到的模型如图所示:

图 3-3 模型网格图
3.2.2 计算结果分析
在 JOD 模块中建立屈曲分析模块进行分析,可得到薄壁圆筒的六阶屈曲失 稳载荷因子。
表 2 各阶模态的屈曲载荷因子。
| 模态 | 屈曲载荷因子 |
| 1 | 48.015 |
| 2 | 48.015 |
| 3 | 48.98 |
| 4 | 48.981 |
| 5 | 50.188 |
| 6 | 50.188 |
则取第一阶模态的屈曲载荷因子计算临界载荷。由屈曲载荷因子与临界载荷的关系:Pcr = λ ∗ p
当对薄壁圆筒施加 48.015N/mm 的边载时,圆筒将屈曲失稳。对应的各阶模态云图如下所示:
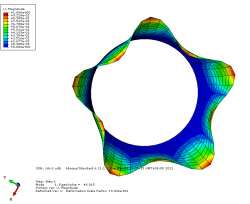
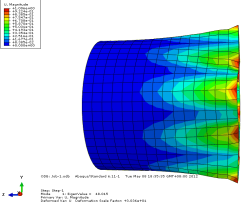
模态1位移轴向和截面方向云图
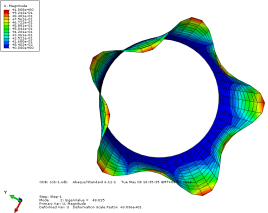
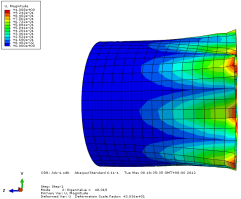
模态2位移轴向和截面方向云图
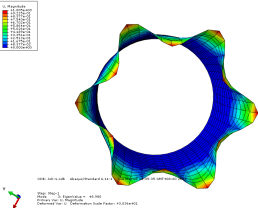
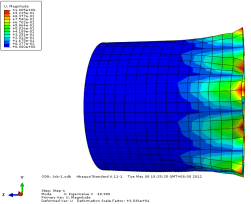
模态3位移轴向和截面方向云图
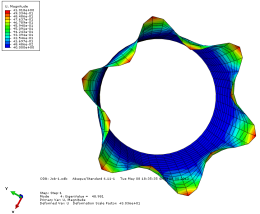
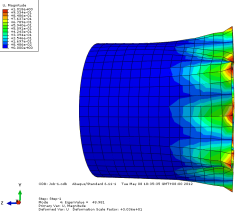
模态 4 位移轴向和截面方向云图
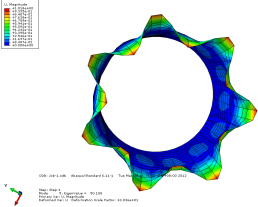
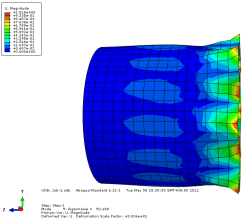
模态 5 位移轴向和截面方向云图
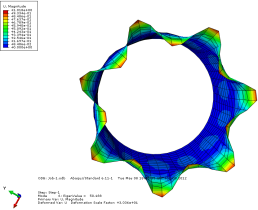
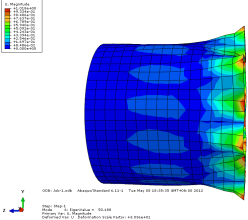
模态 6 位移轴向和截面方向云图
图 3-4 各阶模态云图
由上图可以看出当施加一阶模态的载荷时,圆筒已经屈曲失稳。所以保留一 阶的临界载荷更有现实意义。
4.总结
由算例的计算过程可以得到屈曲载荷因子的大小与划分的网格数和网格类 型有关,网格划分过小会导致计算步骤过多影响计算速度甚至无法计算出结果, 网格过大导致结果不精确。所以在选择网格时应选择适当选择类型和大小。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删