FCN网络在TensorFlow中的实现代码

1、有了神经网络，为什么有CNN？

如果全部使用神经网络，会导致权重过多，计算量增大，无法正常计算。

CNN个人理解为特征的提取，在不损失太多信息量的情况下，减小权重数量，使得网络更容易迭代。其中最重要的2个武器就是局部连接与共享权重

主要搞懂以下2张图的含义，就ok了：

局部连接

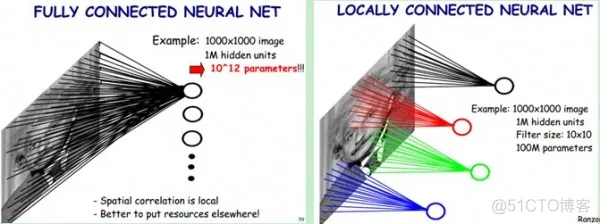
图1：局部连接

全连接：如果我们使用全连接，原图像是1000*1000的图，隐层也设置成1000*1000层。所以全部的权重数为10^12。

局部连接：假设一个隐层的节点，我们只让它观察10*10的数据。所以全部的权重数量就是10^8。

以上就是局部连接的力量。

共享权重

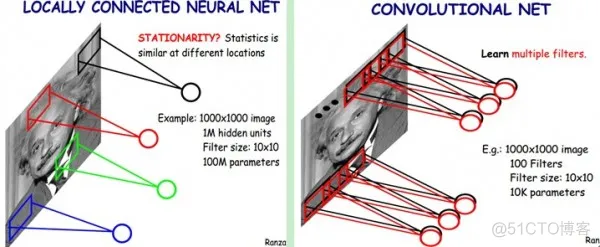
图2：共享权重

我们把上面那个10*10的过滤器（卷积）看做是一种抽取特征的方式，那么我们认为一个种过滤器对应的隐藏层的权重应该一样，所以一下子只需要1个节点。

但认为这样的特征抽取不靠谱，所以通常会用不同的过滤器。图右边就是用了100个filters所以我们就有10*10*100个权重。

池化

顺带把池化层也说一下：

在卷积神经网络中，没有必要一定就要对原图像做处理，而是可以使用某种“压缩”方法，这就是池化，也就是每次将原图像卷积后，都通过一个下采样的过程，来减小图像的规模。

pooling的好处有什么？

1. 这些统计特征能够有更低的维度，减少计算量。

2. 不容易过拟合，当参数过多的时候很容易造成过度拟合。

3. 缩小图像的规模，提升计算速度。

如下图所示，原图是一张500∗500 的图像，经过subsampling之后哦，变成了一张 250∗250 的图像。这样操作的好处非常明显，虽然经过权值共享和局部连接后的图像权值参数已经大大减少，但是对于计算量来说，还是非常巨大，需要消费很大的计算时间，于是为了进一步减少计算量，于是加入了subsampling这个概念，不仅仅使图像像素减少了， 同时也减少计算时间。

举个栗子：以最大池化（Max Pooling）为例，1000×1000的图像经过10×10的卷积核卷积后，得到的是991×991的特征图，然后使用2×2的池化规模，即每4个点组成的小方块中，取最大的一个作为输出，最终得到的是496×496大小的特征图。

下采样，即池化，目的是减小特征图，池化规模一般为2×2。常用的池化方法有：

Pooling算法

最大池化（Max Pooling）。取4个点的最大值。这是最常用的池化方法。
均值池化（Mean Pooling）。取4个点的均值。
可训练池化。训练函数 f ，接受4个点为输入，出入1个点。

由于特征图的变长不一定是2的倍数，所以在边缘处理上也有两种方案：

保留边缘。将特征图的变长用0填充为2的倍数，然后再池化。
忽略边缘。将多出来的边缘直接省去。

2、内存估算方法

核心思想：一个正向传播的权重为4比特，反向传播需要8比特进行计算所需要的内存。显内存约等于bach*权重数量*12比特

3、TensorFlow实现代码

登录后复制

from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
sess = tf.InteractiveSession()
mnist = input_data.read_data_sets('MNIST_data',one_hot=True)

def compute_accuracy(v_xs, v_ys):
    global prediction
    y_pre = sess.run(prediction, feed_dict={xs: v_xs, keep_prob: 1})
    correct_prediction = tf.equal(tf.argmax(y_pre,1), tf.argmax(v_ys,1))
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    result = sess.run(accuracy, feed_dict={xs: v_xs, ys: v_ys, keep_prob: 1})
    return result

def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)

def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)

def conv2d(x, W):
    # stride [1, x_movement, y_movement, 1]
    # Must have strides[0] = strides[3] = 1
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

def max_pool_2x2(x):
    # stride [1, x_movement, y_movement, 1]
    return tf.nn.max_pool(x, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME')

# define placeholder for inputs to network
xs = tf.placeholder(tf.float32, [None, 784]) # 28x28
ys = tf.placeholder(tf.float32, [None, 10])
keep_prob = tf.placeholder(tf.float32)
x_image = tf.reshape(xs, [-1, 28, 28, 1])
# print(x_image.shape)  # [n_samples, 28,28,1]

## conv1 layer ##
W_conv1 = weight_variable([5,5, 1,32]) # patch 5x5, in size 1, out size 32
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1) # output size 28x28x32
h_pool1 = max_pool_2x2(h_conv1)                                         # output size 14x14x32

## conv2 layer ##
W_conv2 = weight_variable([5,5, 32, 64]) # patch 5x5, in size 32, out size 64
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2) # output size 14x14x64
h_pool2 = max_pool_2x2(h_conv2)                                         # output size 7x7x64

## fc1 layer ##
W_fc1 = weight_variable([7*7*64, 1024])
b_fc1 = bias_variable([1024])
# [n_samples, 7, 7, 64] ->> [n_samples, 7*7*64]
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

## fc2 layer ##
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
prediction = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

# the error between prediction and real data
cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys * tf
.log(prediction),reduction_indices=[1]))       
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={xs: batch_xs, ys: batch_ys, keep_prob: 0.5})
    if i % 50 == 0:
        print(compute_accuracy(mnist.test.images, mnist.test.labels))

0.1546
0.814
0.8882
0.9064
0.9195
0.9315
0.9409
0.9426
0.9481
0.9508
0.9566
0.9552
0.9582
0.9602
0.9627
0.9654
0.9642
0.9652
0.9681
0.9665

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删