iSolver案例：桁架结构的跳跃失稳分析

引言：跃越失稳失稳是不同于分支点失稳和极值点失稳的一种失稳方式，它既无平衡分岔点，又无极值点，它是在丧失稳定平衡之后跳跃到另一个稳定平衡状态。

比如，上图中所示为一种很常见的发夹，一般状态是这样左上排的样子，但是在使用时需要先掰一下。这一掰，发夹先发生大的弹性变形，然后在与初始相反的弯曲状态下保持平衡，变成右下排的样子。这就是一个很简单常见的跃越失稳现象。

下文将使用abaqus和isolver两个求解器，计算典型的跃越失稳问题，来测试isolver软件的计算精度。

1、简单空间桁架

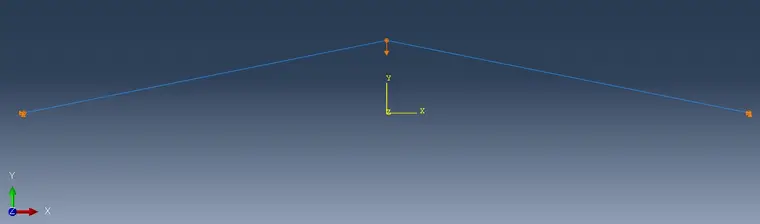
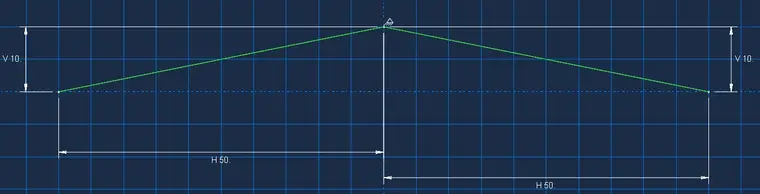
如图是一个包含两根杆件的平面桁架，在顶部节点向下加一集中力P。若仅考虑几何非线性，则为一经典的越跃失稳问题。荷载与顶部节点位移的理论关系为：

1)有限元模型

有限元模型共三个节点，两个单元，单元类型为T3D2。左右两侧节点约束x、y、z三个方向的平动自由度，中间节点约束x、z方向的平动自由度。

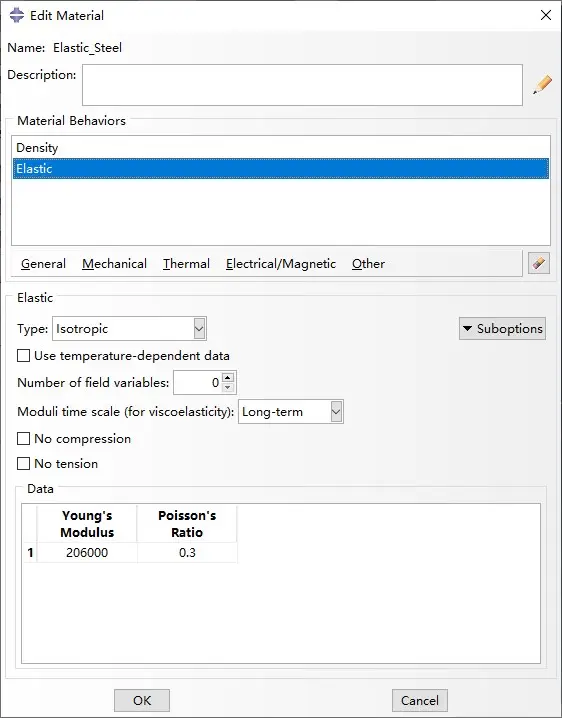
材料本构：使用线弹性材料，如下所示

2）加载

跃越失稳问题是比较难求解的非线性问题，一般采用弧长法求解，为方便收敛本次改用位移加载，使用一般的静力求解方式。

3）求解设置

注意打开几何大变形开关；要在历史输出中输出中间节点的反力和位移，方便绘制荷载位移曲线。

4）结果

最后荷载步的位移和应力云图如下所示。

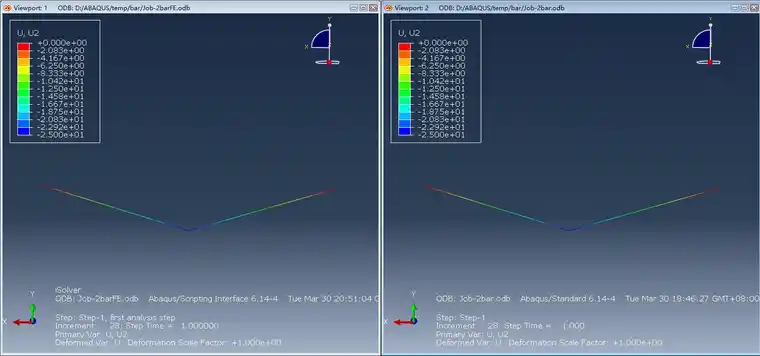
y向位移(左:isolver,右:abaqus)

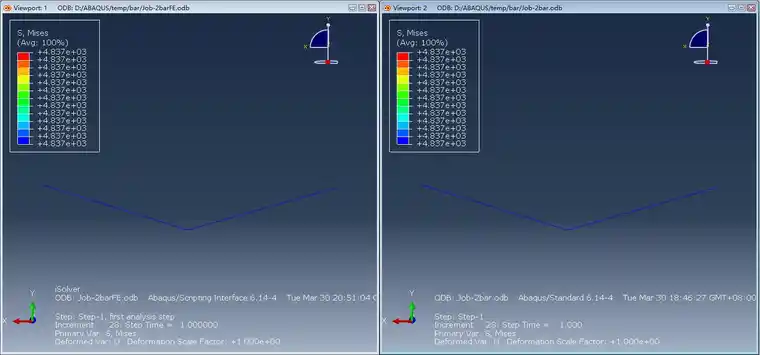
Mises等效应力(左:isolver,右:abaqus)

由图可见，两种软件求解的应力和位移结果完全吻合。

将中间节点的荷载位移曲线的理论解、abaqus解、isolver解画于同一幅图中，如下所示。

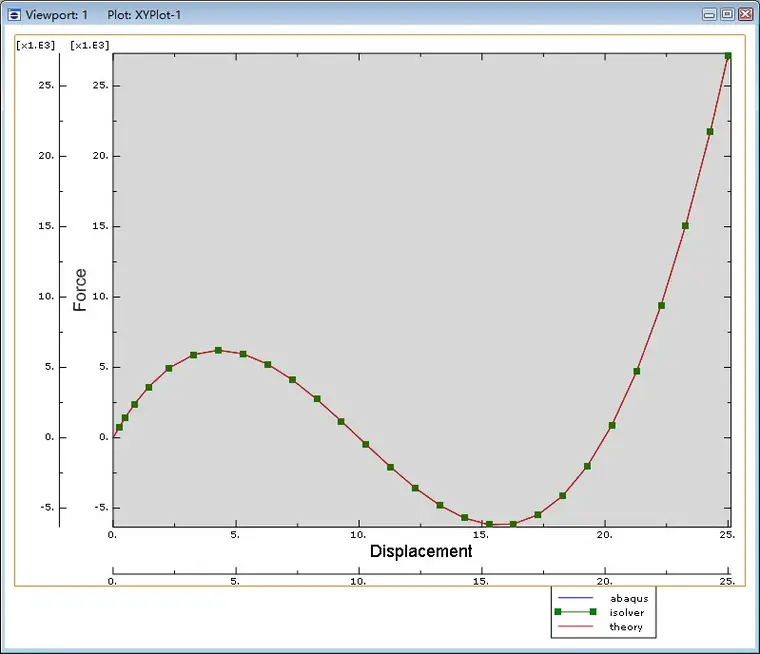
可见，理论解、abaqus解、isolver解的三条曲线弯曲几乎完全重合。

2、空间桁架

1）有限元模型

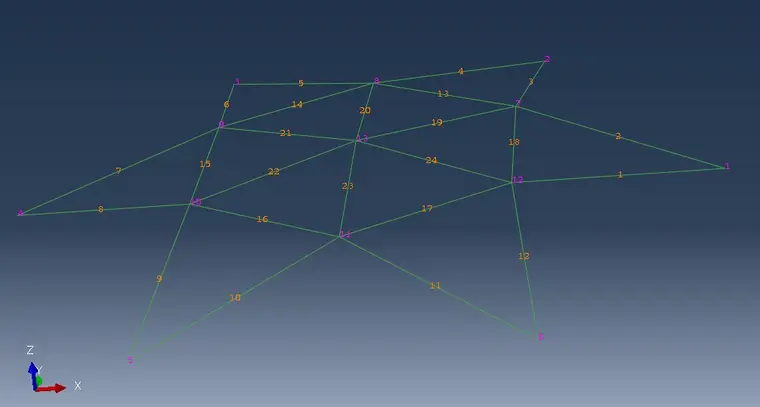
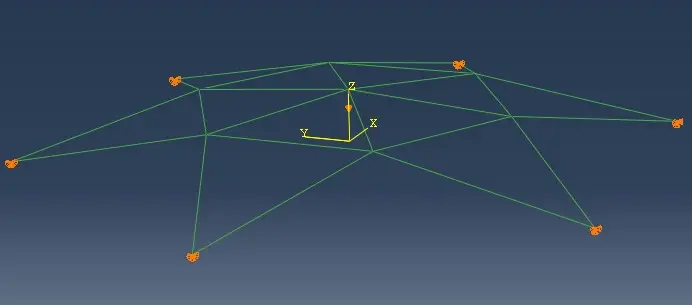
建立如下所示的空间桁架模型。由于杆件空间位置较为复杂，但是规律性强，我们采用inp文件直接建立模型。

节点的参数

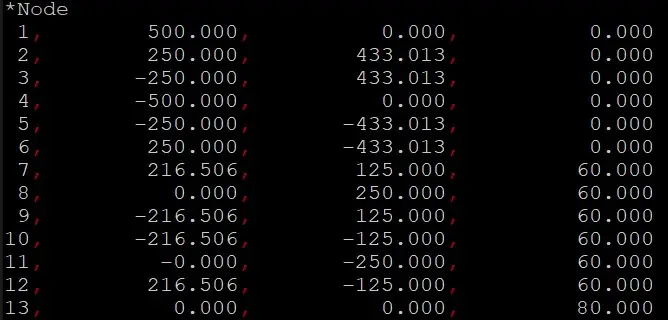
1~6号节点是最下层的节点，7~12是中间层节点，13是底层节点。

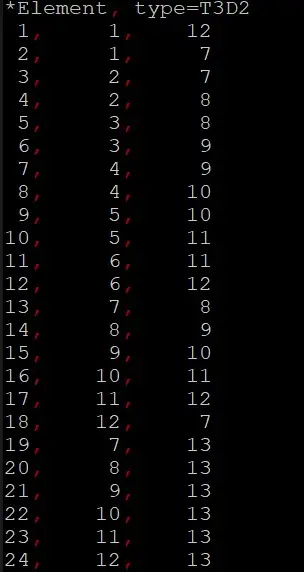
单元参数，使用T3D2单元

2）材料和截面

全部杆件采用相同的材料和截面。截面积为317，弹性模量2.06e5，泊松比0.3.

3）边界条件

底层1~6节点约束x、y、z三个方向的平动自由度，在顶部13号节点施加竖向的强制位移，作为外荷载。

4）求解设置

注意要打开大变形开关，要输出顶部节点的反力和位移

5）结果

位移和应力云图如下所示，两种软件求解结果完全吻合。

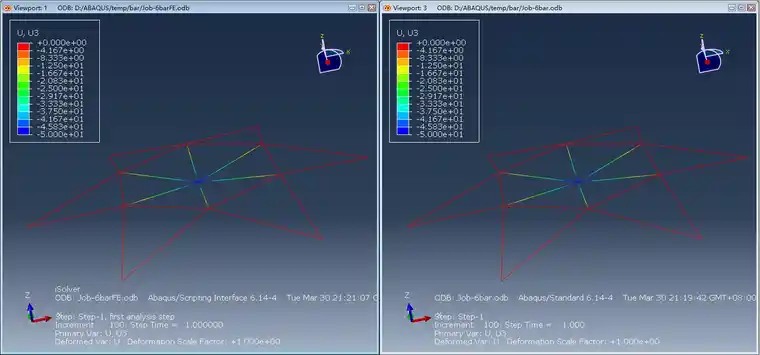
z向位移(左:isolver,右:abaqus)

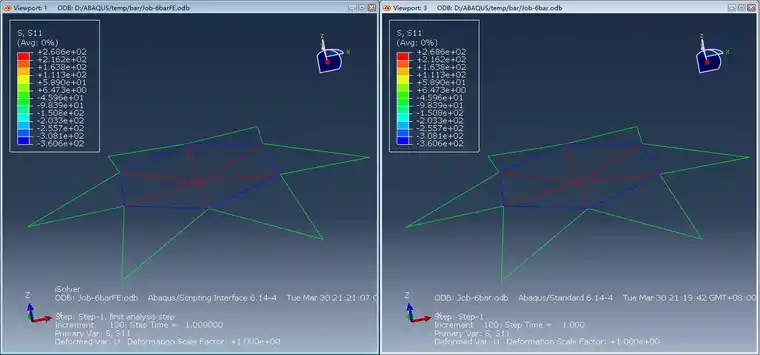
轴向应力(左:isolver,右:abaqus)

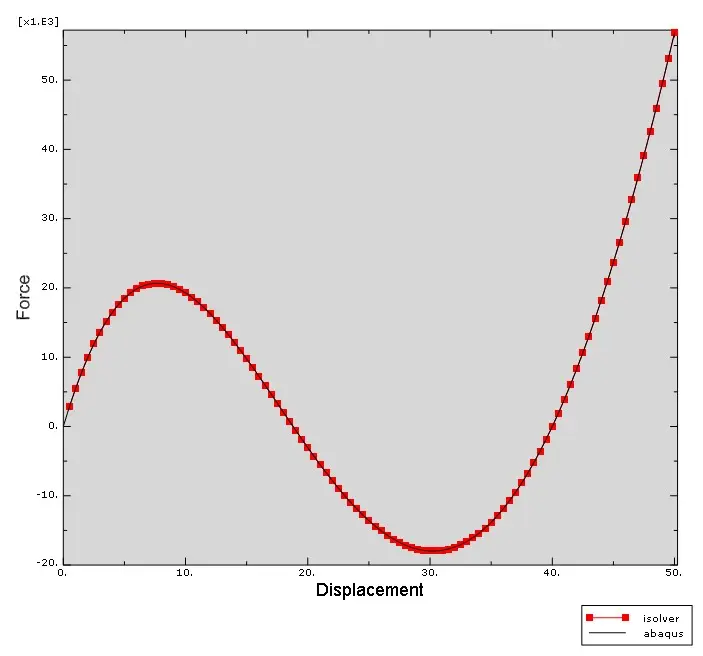
顶部节点的荷载位移曲线如上所述。可见，理论解、abaqus解、isolver解的三条曲线弯曲几乎完全重合。

3、结论

iSolver软件在上述两个问题的求解中有足够的求解精度。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删