1. 引言
iSolver为一个完全自主的面向工程应用的通用结构有限元软件,对标Nastran、Ansys、Abaqus设计和实现,具备结构有限元常用分析类型和单元、材料、载荷等基础算法组件,精度和Abaqus一致。本文以六边形蜂窝芯子受压刚度分析为例,演示iSolver的分析流程,并将iSolver和Abaqus计算结果进行对比。
2. 模型背景
此案例为六边形蜂窝芯子受压刚度的静力学分析,分析对象为典型六边形蜂窝芯子受压刚度,该模型采用自下而上方法建模,截面形状规则,由于蜂窝壁板较薄,因此模型采用壳单元模拟。该蜂窝结构材料铝,其弹性模量为70000MPa,泊松比为0.3。
3. 建模
六边形蜂窝截面规则,因结构特点决定蜂窝壁板存在两种厚度,不同厚度为两倍关系,结构具体形状及厚度分布如下:

为保证模型的求解精度和求解效率,整体采用四边形网格,单元类型选用壳单元S4R,模型共划分为28842个节点和30920个单元。有限元网格如下图所示。
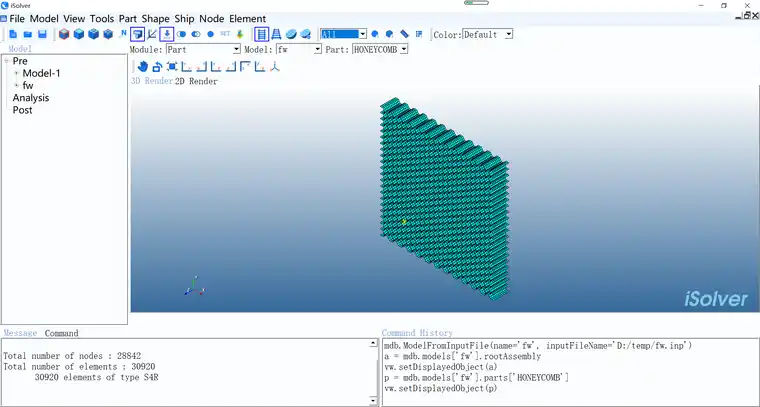
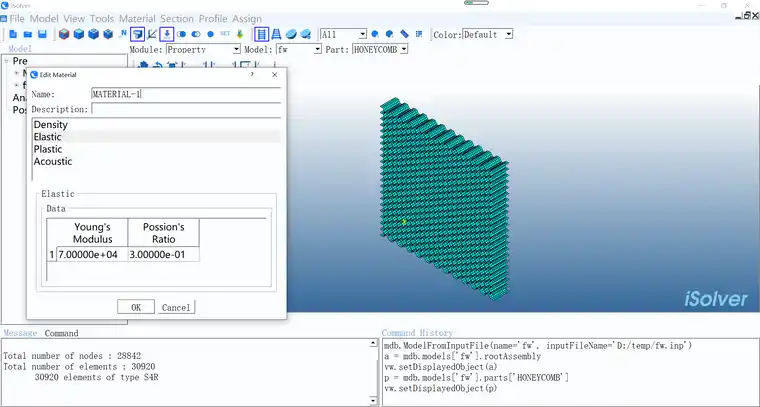
模型采用毫米单位制,蜂窝格孔边长为4mm,厚度分别为0.05mm和0.1mm,材料属性设置如下
蜂窝芯子假设受载形式为W向受压,即一端固支、另一端施加0.01MPa的压力载荷,具体形式如下图所示。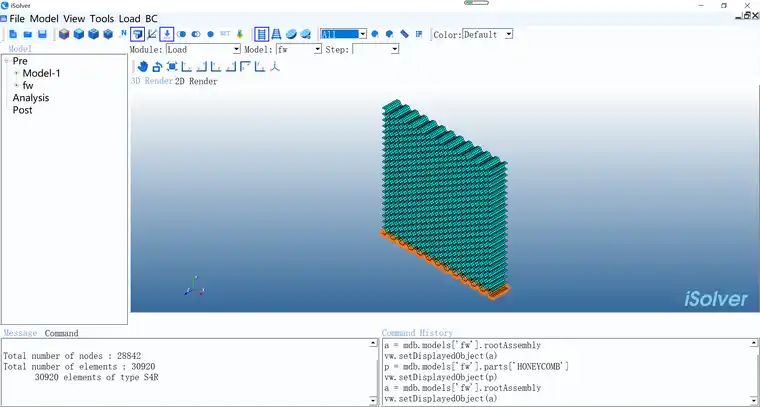
4. 结果对比
1) 应力
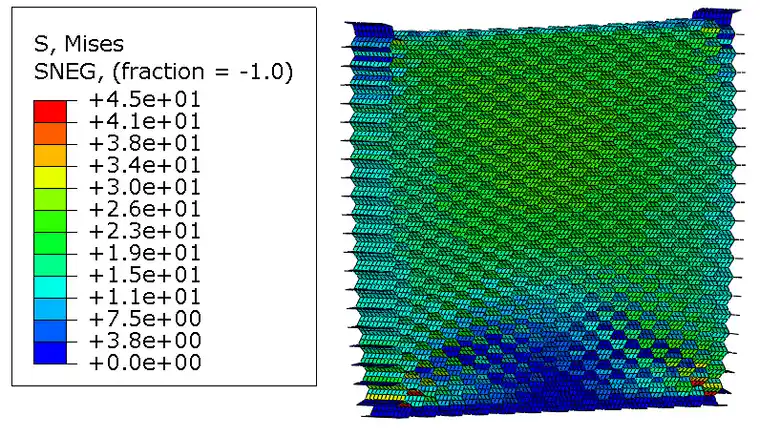
a) 视图1(米塞斯应力)
iSolver结果:

Abaqus结果:
2) 总应变
iSolver结果:

Abaqus结果:
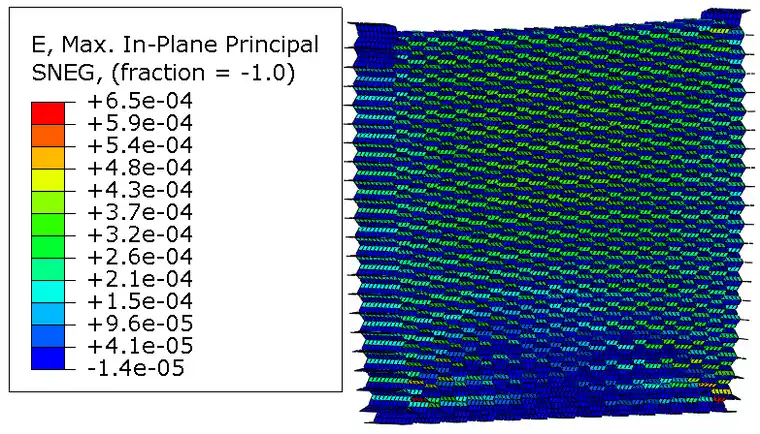
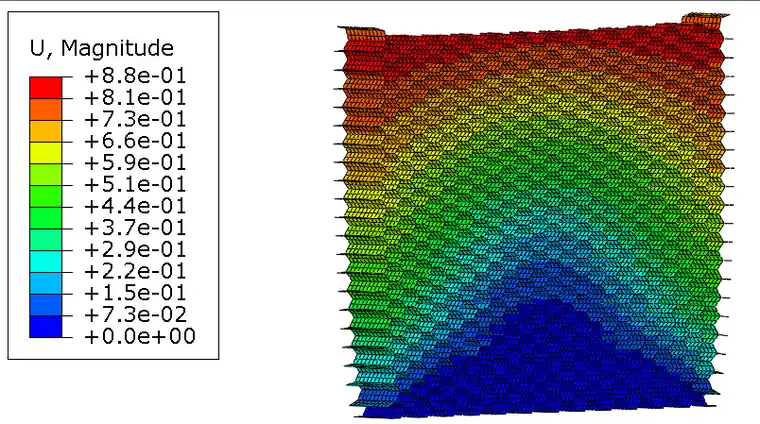
3) 位移
iSolver结果:

Abaqus结果:
5. 结果对比总表如下
由以上结果云图分析可知,iSolver和ABAQUS两个求解器对同一模型分析的结果同一性较好,应力应变的最值发生位置一致,具体数值分析见下表。
| iSolver | ABAQUS | |
| 应力 | 4.512E+01 | 45 |
| 应变 | 6.485e-4 | 6.5e-4 |
| 位移 | 8.803e-1 | 8.8e-1 |
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删