1 引言
近年来,预制装配式建筑随着新建筑技术和材料的不断发展与进步,预制装配式建筑得到了广泛的应用。在许多建筑工业化发达的国家,预制装配式建筑经历了长期的实验和应用,现代化的预制装配式建筑产品已经可以高度集成建筑的各种功能,而且建筑的形式和构件非常精致。
我国建设需求量大、建设速度快,很有必要发展预制装配式建筑,那么对预制装配式结构节点构造要求及吊装工艺也越来越高。传统预制装配式结构吊装成本较高,吊装速度与精度低,这给建筑施工带来了很大的困难,预制装配式建筑吊装要想实现产业现代化,对吊装方法及连接节点等细部构造设计还需进一步创新研究,为此本发明在此问题的基础上根据实际施工的创新作出了相关创造。
结合现有技术而言,目前的装配建筑预制型钢混凝土中间柱梁节点预应力筋交错张拉锚固构造主要存在的问题是:未开发及采用叠合预应力技术,无法有效改善梁柱节点受力特性,无法保证梁柱节点整体性受力要求,且节点抗负弯矩效果较差;目前的装配建筑预制型钢混凝土中间柱梁节点预应力筋交错张拉锚固构造的施工方法存在的问题是:吊装成本较高,吊装速度与精度低,这给建筑施工带来了很大的困难。
在许多实际工程中,比如固体力学中的位移场分析、流体力学中流体的场分析等等都可以看作是在一定边界条件下求解微分方程的问题。但是由于控制微分方程的复杂程度或者边界条件和初始条件确定的复杂性,我们一般不易求得精确的解析解。解析解是一种精确的行为,但是数值解是在节点的离散点上近似于解析解。为了解决这类问题,我们通常都是保留这种问题的复杂性,然后借助于各种有效的数值计算的方法来获得符合工程实际的数值解,此类方法称为数值模拟技术。目前实际工程应用中,运用最广泛的数值求解方法可以划分为:有限单元法、有限差分法。随着计算机的高速发展和广泛应用,人们已经普遍的采用计算工具来处理复杂的计算问题,而有限元方法便是其中非常行之有效的数值方法。
有限元法是一种高效的计算方法,人们通常运用它解决各种复杂的工程分析问题。实际上著名的数学家库朗德第一次提出了可以在定义域内分片地使用展开函数来表达其上的未知函数,实际上有限元就是这样做的,这也是实现有限元方法的一个重要理论。20世纪中叶,航空领域中设计师们由于无法使用传统的方法来了解飞机的应力、应变等问题。波音公司首次提出了将机翼离散成三角形板块集合的方法来进行分析,这其实就是一种有限元的思想。美国著名的卡拉夫教授和我国的冯康教授均在自己的论文中提出了“有限元”这样的名词。有限元法从此正式走进了人们的视野中。
钢筋混凝土由混凝土和钢筋这两种性质不同的材料组合而成,其性质复杂,用传统的解析方法难以对其进行分析。随着计算机技术和有限元方法的发展,有限元分析已经成为研究钢筋混凝土结构的一个重要手段。有限元分析(Finite Element Analysis,简称FEA,)通过利用数学近似方法对真实物理系统进行仿真分析,从而将复杂问题转化为简单问题进行求解。
这里主要采用大型商用有限元分析软件ABAQUS进行有限元分析。ABAQUS美国达索公司旗下产品,是一款功能强大、应用很广的有限元分析软件,其可用于解决从简单线性分析到复杂非线性分析等各类问题。ABAQUS拥有一个丰富多样的单元库和材料模型库,可模拟多种工程材料的性能,其中包括金属、复合材料、钢筋混凝土、高分子材料、泡沫材料以及土壤和岩石等地质材料,作为通用的模拟工具,ABAQUS除了能解决大量结构问题,还可以模拟其他工程领域的许多问题,例如热传导、质量扩散、热电耦合分析、声学分析、岩土力学分析等。
结构分析中非线性问题主要包括几何非线性问题和材料非线性问题,其在钢筋混凝土结构分析中同时存在。其中,几何非线性是指结构产生较大位移,形状也相应发生明显变化,以致平衡方程不能按照原结构的形状列出,必须按照变形后的结构形状来列,这时就必须考虑结构几何非线性。材料非线性则是指材料本身具有非线性应力—应变关系,钢筋混凝土受压时出现弹塑性应变,受压时开裂、混凝土收缩和徐变及钢筋与混凝土间产生滑移等均属于材料非线性问题。针对这些问题,本文借助了ABAQUS本身强大的非线性分析功能对其进行处理,得到了相应结果。
2 数值模型
2.1 模型建立
为验证型钢-钢绞线的新型预制装配式梁柱节点在受力和抗震性能方面与传统节点相比具有优势,采用ABAQUS有限元分析软件分别建立了传统梁柱节点和强化梁柱节点有限元模型,见图1。传统梁柱节点模型主要由混凝土和钢筋骨架组成,梁选用C30混凝土,柱选用C50混凝土,梁截面尺寸为600mm×1000mm,柱截面尺寸为800mm×800mm。强化梁柱节点只是在传统梁柱节点基础上增加了型钢和预应力筋。型钢插入柱里作为预应力锚固端,高为1600mm,其中400mm插入下柱内,上面200mm插入上柱。每根梁设置两束预应力筋,每束由7根直径15.2mm的预应力钢绞线组成,钢绞线的极限抗拉强度标准值为1860MPa。每根钢绞线的张拉力F=195.30kN,则7根钢绞线组合而成的预应力筋的张拉力为F=1367.1kN。预应力筋左端锚固于型钢,右端张拉锚固于梁端下部。
ABAQUS有限元分析软件并不进行自动单位换算,用户通过自行制定几个物理量纲,以得到其他相应的物理单位。常用的单位如表1所示,由于模型尺寸较为精细,加之土木工程实际中常以mm作为长度单位,因此选取第一行的单位制来建立有限元模型。
表1 ABAQUS单位量纲
| 量 | 长度 | 力 | 质量 | 时间 | 应力 | 能量 | 密度 |
| SI/mm | mm | N | t | s | MPa(N/mm2) | mJ(10-3J) | t/mm3 |
| SI/m | m | N | Kg | s | Pa(N/m2) | J | kg/m3 |
| SI/cm | cm | N | 10²kg | s | N/cm2 | J | 10²kg/cm3 |
a)混凝土构件

b)钢筋骨架

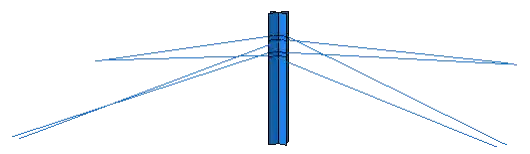
c)型钢-钢绞线
图1 有限元模型
2.2 材料本构
1)混凝土本构关系
ABAQUS有限元软件中内置三种材料模型来描述混凝土在低围压状态下的力学行为,三种材料本构模型依次为:混凝土弥散开裂模型(Concrete Smeared Cracking,简称CSC)、混凝土脆性开裂模型和混凝土损伤塑性模型(Concrete Damaged Plasticity,简称CDP)。三种材料本构模型均适用于结构单元类型为梁单元、壳体单元、桁架单元和实体单元的混凝土及钢筋混凝土结构。CSC模型主要用于混凝土在低围压下承受单调应变,该模型通过赋予线弹性模型的弹性属性来使用;混凝土脆性开裂模型假定材料在压缩时为线弹性,主要用于主导失效模式为受拉开裂的情况;CDP模型是基于连续、塑性的损伤模型,模型的损伤通过定义受拉损伤和受压损伤因子、拉压等效塑性应变和拉压刚度恢复系数等参数来反映。
CDP模型中,单轴方向上混凝土在拉应力或者压应力的关系为:
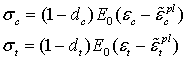
单轴循环荷载作用下,混凝土内部会形成微裂缝,随着裂缝的开合,以及微裂缝之间会产生相互作用关系,使得混凝土在不同类型荷载作用下的刚度衰减机理异常复杂。当混凝土微裂缝之间所受的拉应力变为压应力时,裂缝会紧闭,混凝土的受压刚度得到恢复;当由微裂缝之间的压应力力变为拉应力时,微裂缝张开,受拉刚度未恢复,故CDP模型中混凝土的弹性模量通过弹性刚度退化因子d描述,如图2所示。
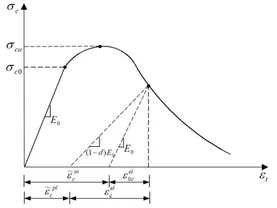
a)受压弹性刚度变化
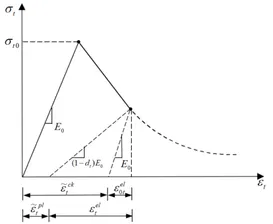
b)受拉弹性刚度变化
图2 CDP模型中受压受拉刚度变化
2)钢筋本构关系
结构进行有限元分析时,通常假定钢筋的受拉应力-应变关系与受压应力-应变关系相同,故采用相同的弹性模量。结构分析时,通常将钢筋的本构关系简化为以下四种形式,即理想弹塑性模型、双线性模型、三折线模型和全曲线型模型。根据有限元计算结果,采用双线性模型计算的精度较好,故选择此模型作为钢筋的应力应变关系模型。
2.3 单元选取和网格划分
1)单元选取
有限元建模中,选择合适的单元类型有助于提高计算的精确性,能更好的模拟结构实际的受力情况。ABAQUS 提供了丰富的单元库来解决不同类型的问题,本文建模过程中主要运用了实体单元、桁架单元和壳单元。本文的有限元模型中混凝土部分选用三维实体 C3D8R 单元,C3D8R单元为三维八节点线性减缩积分单元,适用于网格扭曲较大的大应变分析,得到的位移结果较精确,但减缩积分单元会引起“沙漏现象”,需要引入沙漏刚度、细化网格、在厚度方向划分四个以上的单元等措施来控制“沙漏现象”。钢筋和预应力筋选用桁架单元 T3D2,T3D2 单元为两节点线性三维单元,只能承受拉、压荷载,不能传递弯矩和剪力。型钢采用三维壳单元S4R。
2)网格划分
网格划分是影响有限元模型计算和精度的重要因素,合理有效的网格划分既能够提高计算效率又能够很好的保证计算精度,ABAQUS提供多种生成网格的技术,包括结构化(structured)、扫掠(swept)、自由(free)网格划分技术,前二者适用于特殊的拓扑模型和几何体,自由网格划分是较为灵活的网格划分方式,适用于任意的模型形状。节点有限元模型的单元网格划分采用结构化自适应网格划分的方法进行,该方法可以得到规则的六面体或四边形单元,见图3。

图3 网格划分
2.4 边界条件和预应力施加
1)边界条件
柱端和梁端约束X、Y和Z方向的位移,模拟铰接约束。
2)预应力施加
预应力钢筋中的预应力是通过降温进行施加的。
2.5 加载制度
1)柱顶轴压
以0.3为轴压比控制值,在柱顶施加恒定轴向荷载N。N按下式计算:
N=0.3×fc×A=0.3×23.1×800×800=4435.2kN
2)梁端循环往复加载
保持柱顶的轴力不变,在梁端施加Z向循环往复荷载,见图9。加载按位移控制,在初始加载阶段,每级位移为2mm,每级循环一周。然后每级位移为6mm,每级循环一周。最后每级位移为12mm,每级循环一周,直至节点发生破坏。
3 抗震性能分析
通过分别计算传统梁柱节点与型钢-钢绞线新型预制装配式梁柱节点,其结果如下。
3.1 破坏形态
梁柱节点有限元模型中,混凝土、钢筋骨架以及预应力筋的应力云图见图4、7、8。由图可知,传统节点中混凝土的最大应力值为32MPa,钢筋的最大应力值为632MPa;强化节点中混凝土的最大应力值为33.2MPa,钢筋的最大应力值为500MPa。传统节点模型和强化节点模型中的混凝土的最大应力值相差不大,而传统节点模型中钢筋的最大应力值明显大于强化节点模型的,传统节点模型中的部分钢筋已发生破坏,而强化节点中的钢筋还未破坏,只是部分钢筋进入塑性变形阶段。因此,在相同荷载作用下,强化节点更不容易发生破坏。此外,强化节点中预应力筋的最大应力为1860MPa,此时预应力筋已进入弹塑性工作阶段,充分发挥了预应力筋的作用。节点模型中混凝土的受压损伤和受拉损伤云图分别见图5、6。由图可知,在相同荷载作用下,强化节点的损伤更少。

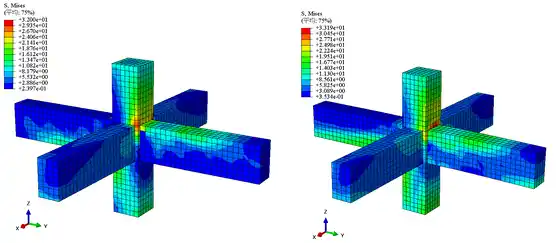
a)传统节点 (b)新型装配式节点
图4 混凝土应力云图
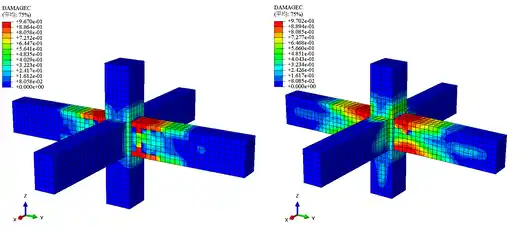
(a)传统节点 (b)新型装配式节点
图5 混凝土受压损伤
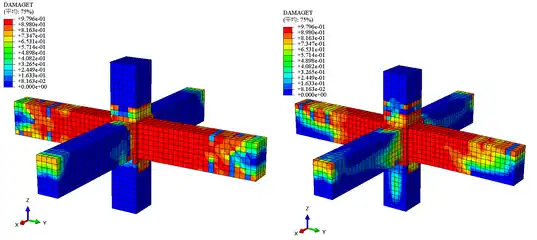
(a)传统节点 (b)新型装配式节点
图6 混凝土受拉损伤
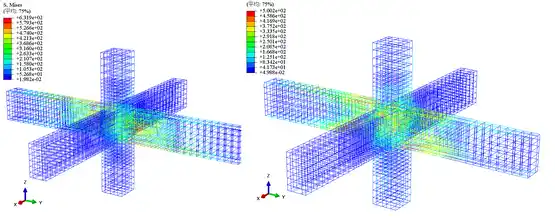
(a)传统节点 (b)新型装配式节点
图7 钢筋应力云图
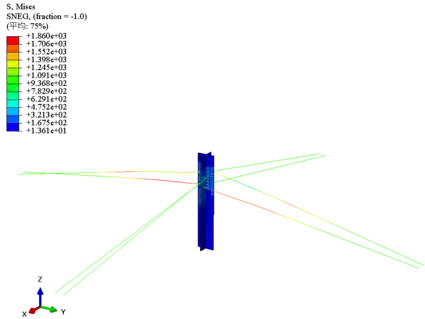
图8 预应力筋应力云图
3.2 滞回性能
滞回曲线是试件在低周往复荷载作用下的荷载—位移曲线,综合体现了结构的抗震性能,也是进行结构弹塑性动力反应的主要依据。由滞回曲线上各级同向(拉或压)加载第一圈循环的荷载极值点依次相连得到的包络曲线称为骨架曲线。骨架曲线是每级循环加载的荷载—位移曲线达到最大峰值点的轨迹,可以反映构件在不同阶段受力与变形的关系,也可反映构件的强度、刚度、延性、耗能及抗倒塌能力等。滞回曲线和骨架曲线也是确定恢复力模型特征点的重要依据。
梁柱节点的滞回曲线和骨架曲线对比分别见图9、10。由图可知,正向加载时,传统节点的承载力在梁端竖向位移为72mm时达到最大值,该值为729.4kN;强化节点的承载力在梁端位移为45mm时达到最大值,该值为763.4kN,强化节点的承载力比传统节点的高5%。负向加载时,传统节点的承载力在梁端竖向位移为58mm时达到最大值,该值为706kN;强化节点的承载力在梁端位移为39mm时达到最大值,该值为1227.8kN,强化节点的承载力比传统节点的高74%。正向加载时,传统节点的初始刚度为52kN/mm,强化节点的初始刚度为55kN/mm,强化节点的初始刚度比传统节点的高6%。负向加载时,传统节点的初始刚度为52kN/mm,强化节点的初始刚度为80kN/mm,强化节点的初始刚度比传统节点的高54%。因此,正向加载时,强化节点的初始刚度和承载力略大于传统节点的,而在负向加载时,强化节点的初始刚度和承载力明显大于传统节点的。由图还可看出,强化节点曲线的包络的面积大于传统节点的,说明强化节点的耗能能力更好。综上,强化节点的刚度、承载力和耗能能力均优于传统节点的。

图9 滞回曲线对比
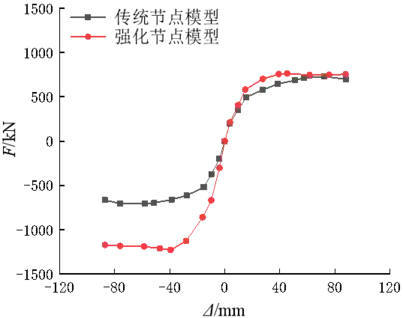
图10 骨架曲线对比
4 结论
为验证装配式强化梁柱节点在受力和抗震性能方面与传统节点相比具有优势,分别建立了传统梁柱节点和强化梁柱节点有限元模型,分析了它们的破坏形态和滞回性能。结果表明,在相同荷载作用下,强化节点更不易发生破坏;强化节点的刚度、承载力和耗能能力均优于传统节点的。综上所述,基于型钢-钢绞线的新型预制装配式梁柱节点抗震性能优异,可将其推广运用于工程实践。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删