案例分享：iSolver下的拱桥模态分析实例

引言：结构有限元软件iSolver已发展到一定阶段，现采用结构有限元软件iSolver进行结构分析，iSolver可使用Abaqus作为前后处理工具，本文以桥梁结构的模态分析为例，将iSolver和Abaqus计算结果进行对比，计算实例采用《ABAQUS有限元分析从入门到精通》一书中的经典案例“拱桥结构的模态分析”，比对两种有限元软件的计算结果。

模态分析是研究结构动力特性的一种近代方法，是系统辨别方法在工程振动领域中的应用。通过模态分析方法，可以搞清楚结构物在某一易受影响的频率范围内的各阶主要模态的特性，就可以预言结构在此频段内受外部或内部各种振源作用下产生的实际振动响应。

模态分析的最终目标是识别出系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。因此，模态分析技术的应用可归结为以下几个方面。

1）评价现有结构系统的动态特性。

2）对新产品设计进行结构动态特性的预估和优化设计。

3）控制结构的辐射噪声。

4）诊断及预报结构系统的故障。

问题描述：

下面以一个桥梁为例，对其进行模态分析，分析其固有频率和振型模态，对拱桥的设计具有重要意义。在计算过程中，采用国际单位制：长度（米，m）、质量（千克，kg）、力（牛顿，N）、应力（帕，Pa）、时间（秒，s）

桥模型如图所示。模型为密度=2430kg/m、弹性模量E=52.3×10^6Pa，泊松比v=0.3的线弹性各向同性材料。

图1 桥梁有限元模型

操作：

设定好材料参数后，建立分析步，求解前30阶固有频率和振型。

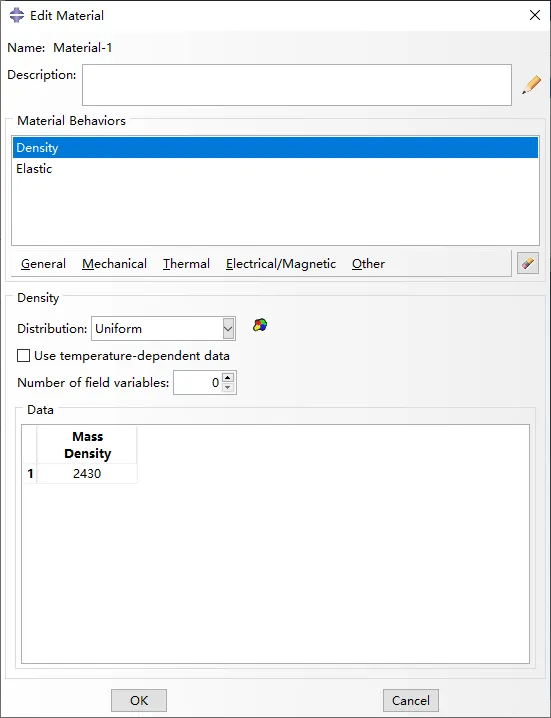
图2 材料参数

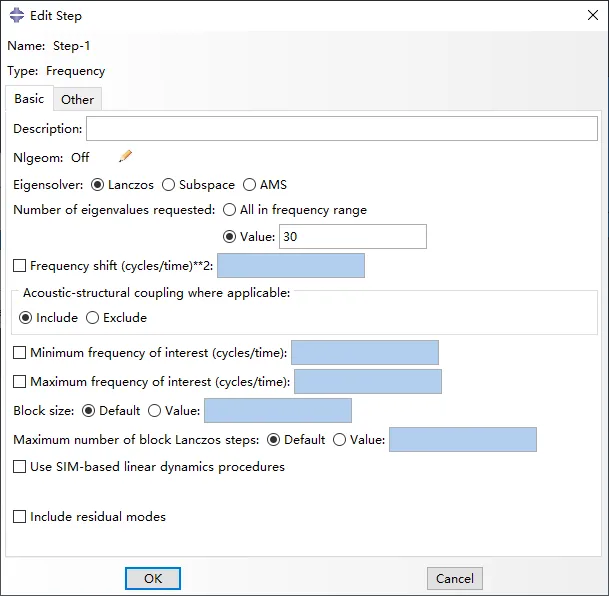
图3 分析步

创建边界条件，约束桥梁底部的6个自由度。

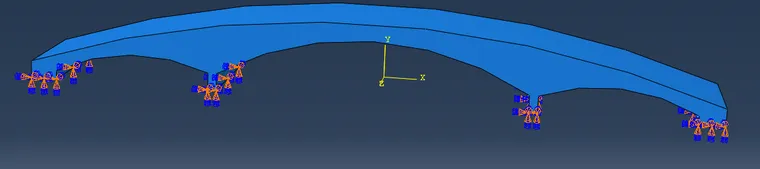
图4 设置边界条件

采用C3D10单元划分网格，网格数量为36959。

图5 划分网格

分别采用Abaqus和iSolver求解器进行计算。

图6分别提交Abaqus和iSolver求解器计算

计算结果对比：

对比两者的计算结果。以下是前30阶固有频率的对比。

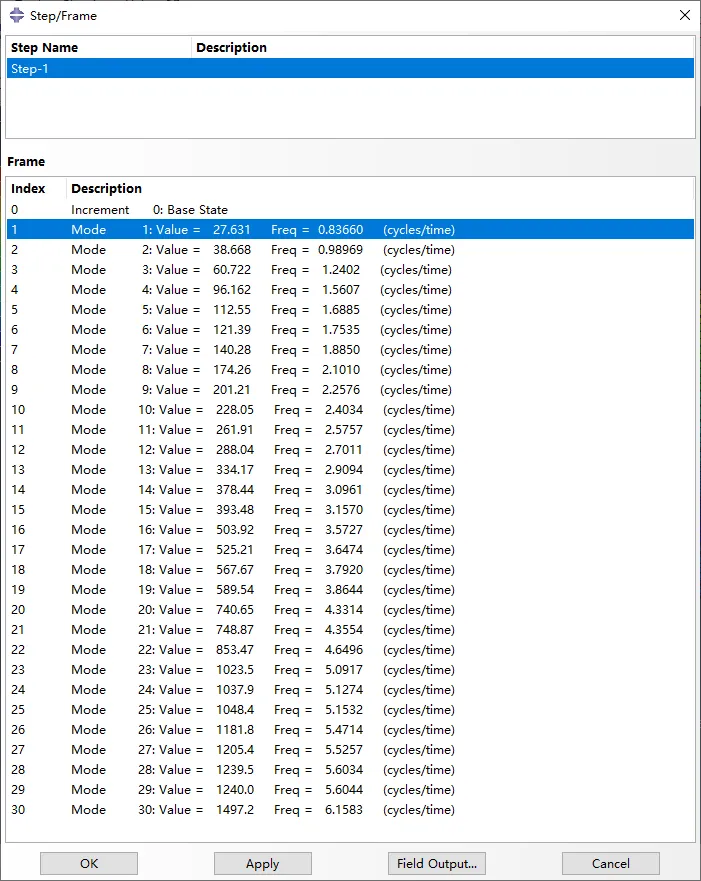
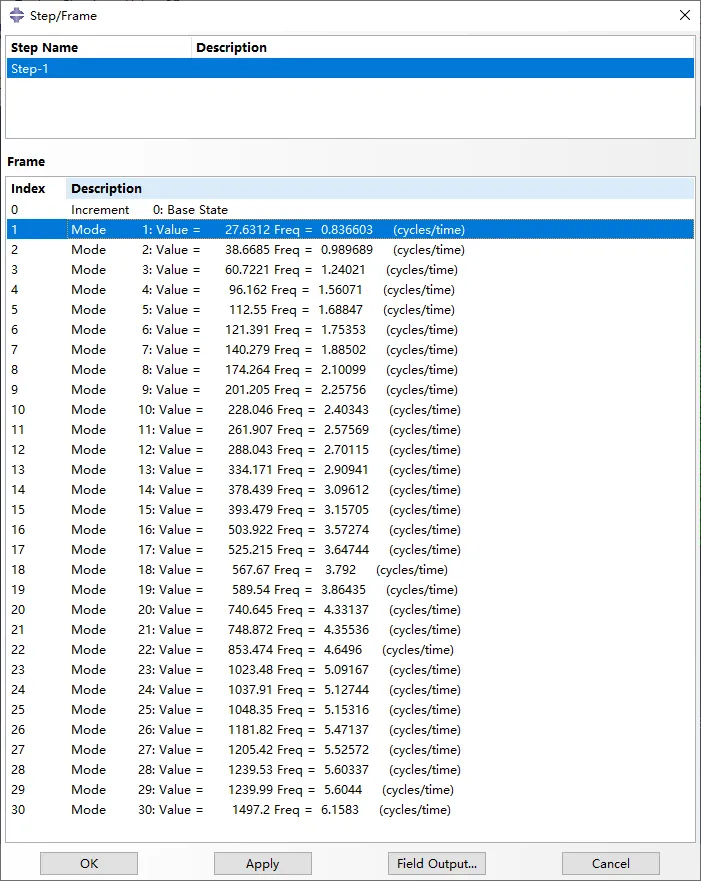
图7  Abaqus和iSolver计算的固有频率对比

一阶振型的对比：

图8  Abaqus和iSolver计算的一阶振型对比

二阶振型：

图9  Abaqus和iSolver计算的二阶振型对比

三阶振型：

图10  Abaqus和iSolver计算的三阶振型对比

由此可见，iSolver与Abaqus求解器计算的模态分析结果基本一致，固有频率和振型计算结果吻合。

从模型的振型图可以看出，对于石拱桥模型来说，当其频率到达固有频率时，其振动幅度远远超过其允许的位移量，这将导致结构的破坏。所以对大型结构进行的模态分析，可以有效地避免结构长期处于共振频率下，达到避免结构破坏的作用。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删