结构有限元软件iSolver已发展到一定阶段,现采用结构有限元软件iSolver进行结构分析,iSolver可使用Abaqus作为前后处理工具,本文以桥梁结构的模态分析为例,将iSolver和Abaqus计算结果进行对比,计算实例采用《Abaqus Tutorial:Natural Frequency Extraction of a Bridge》中的经典案例“桥梁结构的模态分析”,比对两种有限元软件的计算结果。之前采用线弹性实体单元提取了拱桥的模态。这次采用非线性的弹塑性材料,分别用壳单元模拟桥面,用梁单元模拟支柱,提取桥梁模态。
下面以一个桥梁为例,对其进行模态分析,分析其固有频率和振型模态,对拱桥的设计具有重要意义。在计算过程中,采用国际单位制:长度(米,m)、质量(千克,kg)、力(牛顿,N)、应力(帕,Pa)、时间(秒,s),桥模型如图所示。

图1 桥梁有限元模型
操作:
模型为密度=8000kg/m、弹性模量E=210×10^9Pa,泊松比v=0.3的弹塑性各向同性材料。桥面采用壳单元模拟,支柱采用梁单元模拟,需定义梁截面方向。设定好材料参数后,建立分析步,求解前10阶固有频率和振型。
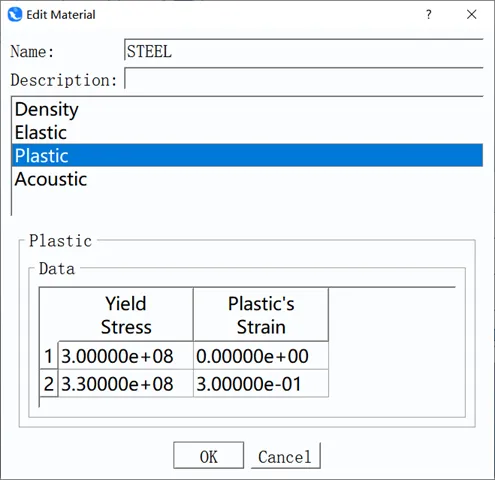
图2 材料参数

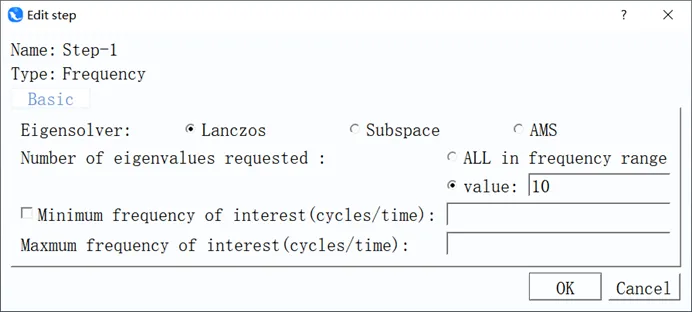
图3 分析步
创建边界条件,约束桥梁底部的6个自由度。
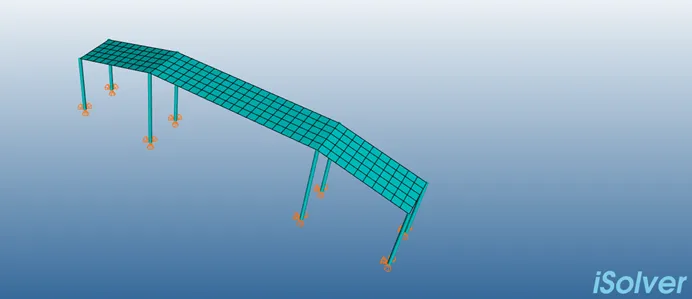
图4 设置边界条件
划分网格,网格数量为272。
图5 划分网格
分别采用Abaqus和iSolver求解器进行计算。
对比两者的计算结果。以下是前10阶固有频率的对比。
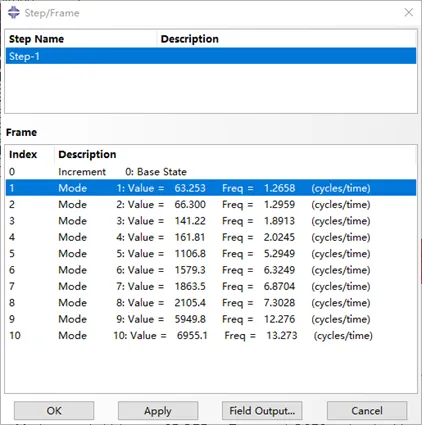
图6 Abaqus前10阶固有频率
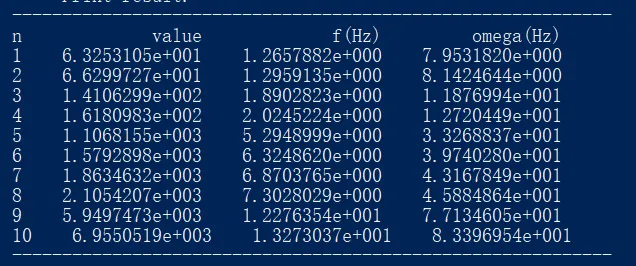
图7 iSolver前10阶固有频率
频率对比总表如下:
| 序号 | Abaqus | iSolver |
| 1. | 1.2658 | 1.26579 |
| 2. | 1.2959 | 1.29591 |
| 3. | 1.8913 | 1.89028 |
| 4. | 2.0245 | 2.02452 |
| 5. | 5.2949 | 5.2949 |
| 6. | 6.3249 | 6.32486 |
| 7. | 6.8704 | 6.87038 |
| 8. | 7.3028 | 7.3028 |
| 9. | 12.276 | 12.2764 |
| 10. | 13.273 | 13.273 |
一阶振型的对比:
Abaqus
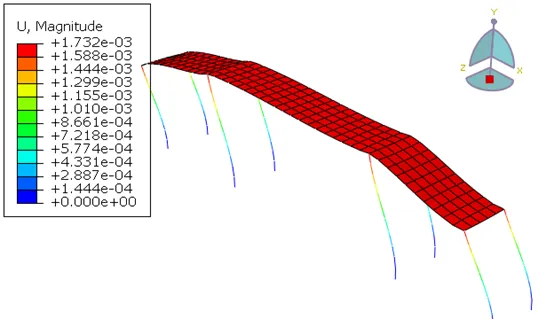

iSolver

图8 Abaqus和iSolver计算的一阶振型对比
二阶振型:
Abaqus
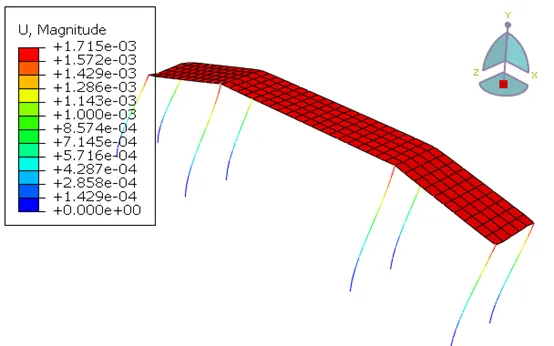

iSolver

图9 Abaqus和iSolver计算的二阶振型对比
三阶振型:
Abaqus
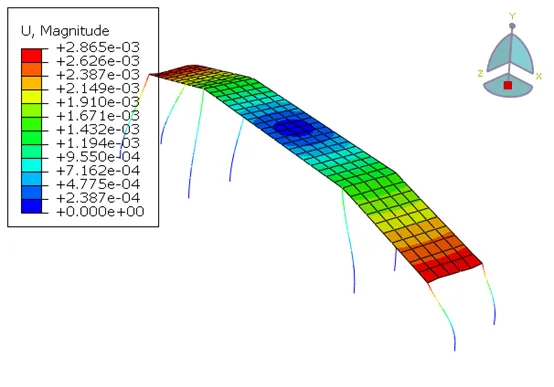
iSolver
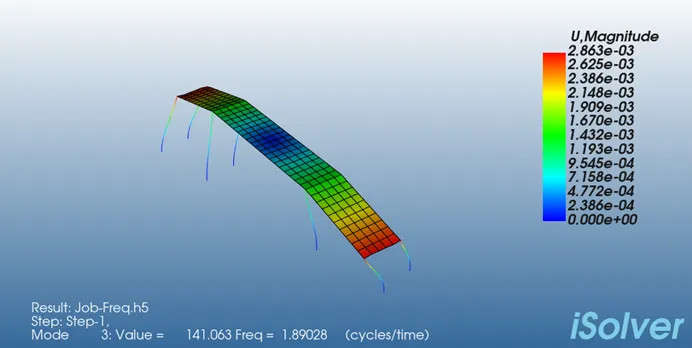
图10 Abaqus和iSolver计算的三阶振型对比
| 模态号 | 频率- ABAQUS | 频率- iSolver | 位移- ABAQUS | 位移- iSolver |
| 1 | 1.2658 | 1.26579 | 1.732E-03 | 1.732E-03 |
| 2 | 1.2959 | 1.29591 | 1.715E-03 | 1.715E-03 |
| 3 | 1.8913 | 1.89028 | 2.8625E-03 | 2.863E-03 |
由此可见,iSolver与Abaqus求解器计算的模态分析结果基本一致,固有频率和振型计算结果吻合。
iSolver为免费软件,且无license限制,最新版免费下载地址如下:
https://www.jishulink.com/content/post/337351
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删