弹簧质量块系统自振分析：Abaqus变形体模拟

以下图系统为例：

其中弹簧长度为10m，质量块的体积为1m*1m*1m。

需要注意的是在建完模型后Abaqus会自动生成jnl文件，但是当将自动生成的文件原封不动地导入Abaqus中的时候会报错：

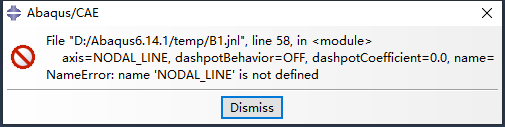
原因已有网友给出了：

因此我给出的链接中的文件是加了from abaqusConstants import*之后的，是可以直接运行的。

结合下图，再说一下建模中的几个点：

首先是固定端通过参考点（RP）来建立，并对该点施加全约束；质量块这里通过立方体来建立，并约束住除了运动方向（水平方向）外的所有自由度。

其次是弹簧的建立在GUI的方式中是interaction-special-springs中来建立。

再次是在定义质量块的属性时，除了给出关键参数密度以外，还需给出弹模等参数（该例中的质量块是输入的钢材的参数）。

最后是在定义分析步时，由于此处分析的是系统的固有动力性质，所选取的是linear perturbation-frequency，并且提取前两阶的结果。

这里的取前两阶结果只是举例。

运行可得前两阶频率和振型：

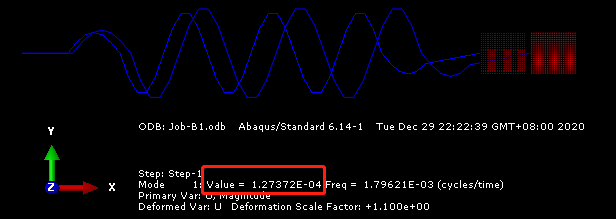
以上图中的value值就是特征值，即为w2。该例的理论解为w2=k/m=1.27389E-4，和Abaqus求解出来的解非常接近。

以上结果同样可以在生成的“结果文件名.dat”文件（该例为Job-B1文件）中查看，如下：

可以看出，dat文件中明确指出第1阶为刚体运动的模态。其实我们所要求的就是刚体运动的模态，即模态1，而模态2从振型图中可以看出来是质量块本身变形的模态，这并不是我们想要的。

有时候，当弹簧的刚度和质量块的弹模取值不恰当时，会出现质量块本身变形为第1阶模态而刚体运动的模态为其他阶的结果（这里可以这样理解，当弹簧刚度过大而质量块的弹模过小的时候，质量块更容易产生本身的变形，频率就越低，最终导致质量块本身的变形模态有可能成为第1阶模态）。可以验证，当减少质量块的弹模为206时，得到的振型图如下：

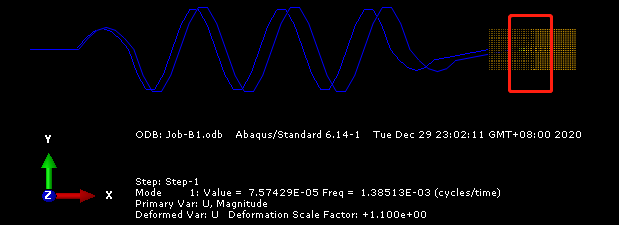
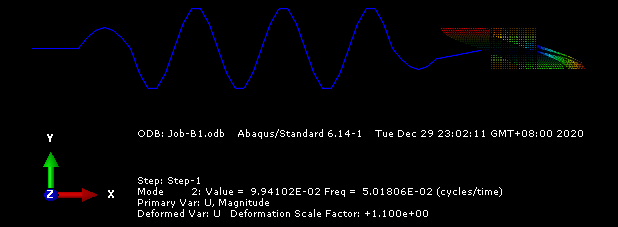
可以看出此时的前两阶模态均包含了质量块本身变形的成分。

并且此时的dat文件中，也不会讲有哪个模态是刚体运动的模态，即这样分析得不到我们需要的模态结果。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删