软件
产品
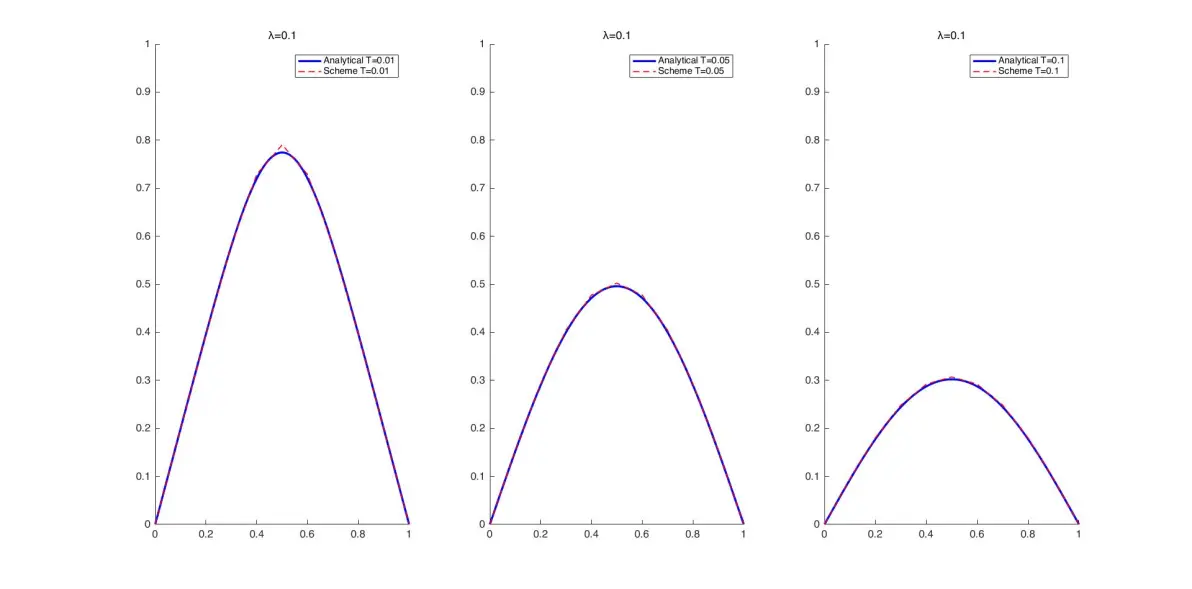
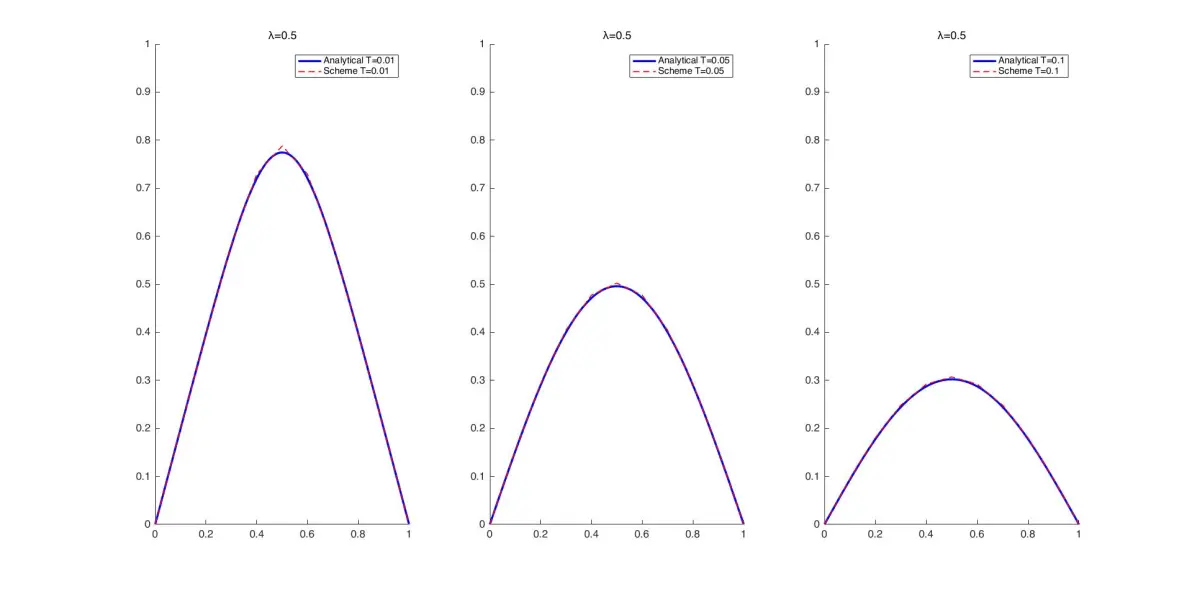
利用Crank-Nicolson格式求解算例一的问题。
备注:Crank-Nicolson格式详见《偏微分方程数值解法》第3版陆金甫编著P78公式(6.17)
以及P90公式(1.8)
======================================================================================================答案===================================
(1)
(2)

(3)
%%偏微分方程有限差分法实习题
%算例二
tic%开始计时
clc
clear all
%==================================================
%输入参数
a=1; %扩散方程常系数a
T=[0.01,0.05,0.1]; %结束时间节点
dx=0.1; %空间步长
x=0:dx:1; %空间范围剖分
dt=0.01; %时间步长
t=0:dt:T(3); %最大时间范围剖分
lambda=dt/dx/dx;%λ
%==================================================
%解析解
xx=0:0.01:1;
for tt=1:size(T,2) %三个时间节点对应的解析解值
ff=zeros(1,size(xx,2));
for i=1:size(xx,2)
uu=0;
for j=1:17 %级数累加,十七次即可满足精度要求
f=sin(j*pi/2)*sin(j*pi*xx(i))*exp(-j*j*pi*pi*T(tt))/j^2;
uu=uu+f;
end
ff(i)=8*uu/pi/pi;
end
subplot(1,3,tt)
hold on
plot(xx,ff,'b-','LineWidth',2)
end
%==================================================
%差分格式解
n=size(x,2)-2;
A=(1+a*lambda).*eye(n);%Crank-Nicolson格式方程组系数矩阵A
cc=-0.5*a*lambda;
for i=2:n
A(i,i-1)=cc;
A(i-1,i)=A(i,i-1);
end
u=zeros(size(t,2),size(x,2)); %给矩阵提前分配内存
u(1,:)=2*x.*(x<=0.5)+2*(1-x).*(x>0.5);%初始条件
for j=2:size(t,2)
B=zeros(n,1); %开始计算列向量B
for i=2:n+1
B(i-1)=u(j-1,i-1)*0.5*a*lambda+u(j-1,i)*(1-a*lambda)+u(j-1,i+1)*0.5*a*lambda;
end
u(j,2:n+1)=Thomas(A,B);%调用追赶法子程序
end
%开始绘图
for i=1:size(T,2)
subplot(1,3,i)
plot(x,u(T(i)/dt+1,:),'r--','LineWidth',1)
str{i}=['Analytical T=' num2str(T(i))];
str1{i}=['Scheme T=' num2str(T(i))];
legend(str{i},str1{i}) %图例
title(['λ=',num2str(lambda)]) %标题
xlim([0 1]); %画个合适的坐标轴
ylim([0 1]);
end
%==================================================
toc %计时结束Thomas子程序详见:
