MATLAB实现数值积分法教程

MATLAB的工具箱提供了各种数值积分方法函数，这些函数是ODE23、ODE45、ODE113和ODE15s。这些函数均是m文件，还有一个函数是ode1.C，是直接用C语言编写的。

   函数ode23( )是用Runge-Kutta法求解微分方程。它是一种采用三阶积分算法、二阶误差估计、变积分步长的低阶积分算法，调用格式为

[T, Y] = ode23 ( 'F', TSPAN, YO, OPTIONS )

其中，F为系统模型文件名，模型为y' = f( t, y )形式；

TSPAN = [ To TFINAL] 为积分计算时间，初值为To，终值为TFINAL；

YO为系统输出初始值；

OPTIONS选项积分计算相对允差 'RelTol' 和绝对允差 'AbsTol'，当缺省时，

    Reltol＝1e-3, AbsTol＝1e-6

T为计算点时间向量，Y为微分方程的解。

函数ode45(  )也是用Runge-Kutta法求解微分方程，它是变步长的一种中等阶次积分算法，调用格式为

[T, Y] = ode45 ( 'F' , TSPAN, YO, OPTIONS )

各项含义同上。

函数ode113( )是变阶的Adams-Bashforth-Moulton，用变阶方法解微分方程，采用多步法，调用格式为

[T, Y] = ode113 ( 'F', TSPAN, YO, OPTIONS )

各项含义同上。

函数odel5s(  )采用改进的Gear法解微分方程，调用格式为

       [T, Y] = odel5s ( 'F', TSPAN, YO, OPTIONS )

各项含义同上。

MATLAB还提供了解微分方程函数ode23s。函数ode1.C是用Euler法求解微分方程。

在SIMULINK中，系统仿真有变步距和固定步距两种工作方式。在变步距仿真中，可选用ode45、ode23、ode113、ose15s和ode23s。在固定步距仿真中，可选用材ode5、ode4、ode3、ode2和ode1。ode5是5阶Runge-Kutta法，ode4是4阶Runge-Kutta法，odel是Euler法。

【例7.1】求微分方程。

用MATLAB编写程序：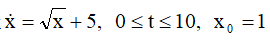

建立一个m函数文件dfun.m

funcion   y＝dhfn ( t，x )

       y＝sqrt ( 3*x )＋5 ;

  在MATLAB COMMAND窗口下运行

  % MATLAB PROGRAM 7-1

  [ t, x ]＝ode23 ( 'dfun'，[0   l0]，1) ;

  Plot ( t，x ) ;

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删