详解Matlab偏微分方程有限差分法应用

考虑如下非齐次热传导问题：

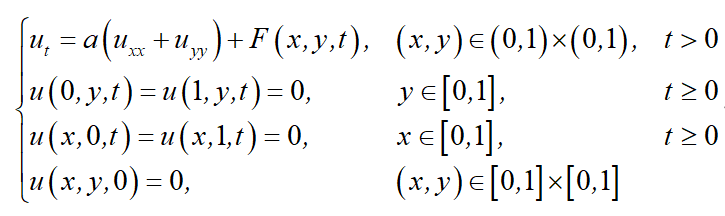
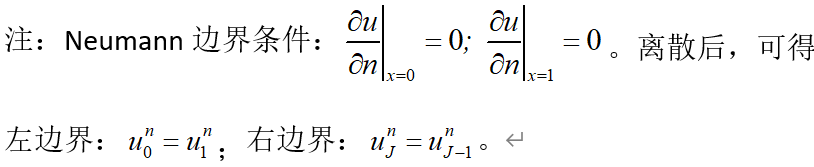
==========答案=========

%%偏微分方程有限差分法实习题
%算例七
tic%开始计时
clc
clear all
%==================================================
%输入参数
T=[0.1,0.2,0.4,0.8]; %结束时间节点
dx=0.05;                 %空间步长
x=0:dx:1;                 %空间范围剖分
dy=0.05;                 %空间步长
y=0:dy:1;                 %空间范围剖分
dt=0.01;                  %时间步长
t=0:dt:T(end);          %最大时间范围剖分
lambda=dt/dx/dx;   %λ
[x,y]=meshgrid(x,y);
%==================================================
%Peaceman-Rachford格式
size(x,2)
u=zeros(size(x,2),size(y,2),size(t,2)); %预先分配内存,同时边界值和初始条件
F=zeros(size(x,2),size(y,2),size(t,2));
for j=1:size(x,2)
    for l=1:size(y,2)
        for n=1:size(t,2)
            F(j, l, n) = sin(5*pi*t(n))*sin(2*pi*x(j,l))*sin(pi*y(j,l));
        end
    end
end
for i=1:size(x,2)-2
    for j=1:size(x,2)-2
        if       i==j
            A1(i,j)=1+lambda;
            A2(i,j)=1-lambda;
        elseif i==j+1
            A1(i,j)=-0.5*lambda;
            A2(i,j)=0.5*lambda;
        elseif i==j-1
            A1(i,j)=-0.5*lambda;
            A2(i,j)=0.5*lambda;
        else
        end
    end
end
for n=2:size(t,2)
    for j=2:size(x,2)-1
            u12=A1\(A2*u(j,2:end-1,n-1)'+0.5*dt*F(j,2:end-1,n-1)');
            u(j,2:end-1,n)=A1\(A2*u12+0.5*dt*F(j,2:end-1,n)');
    end
end
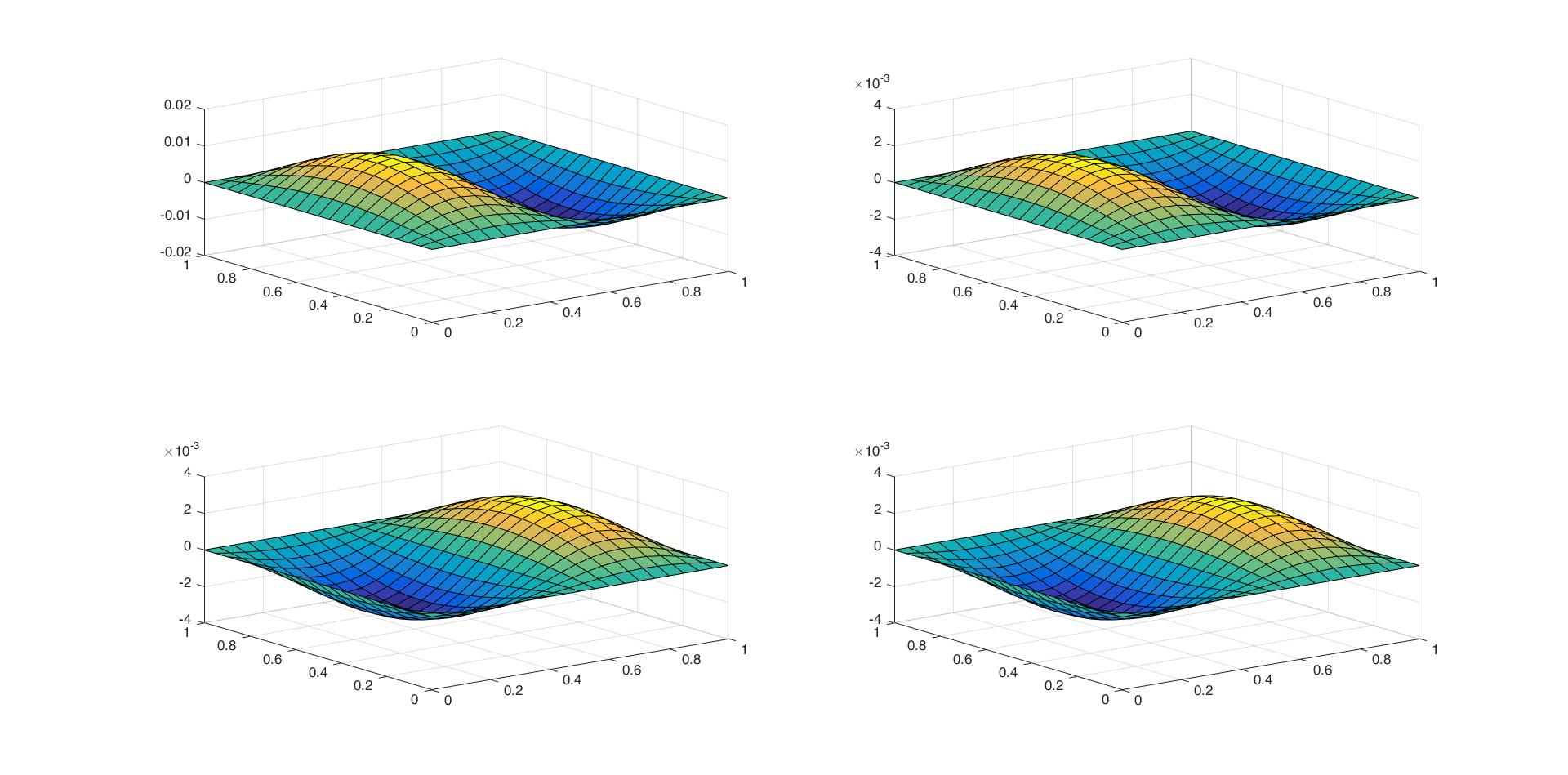
%开始绘图
for i=1:size(T,2)
subplot(2,2,i)
surf(x,y,u(:,:,T(i)/dt+1))
end
%==================================================
toc %计时结束

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删