作者:天生梅纳德(@Maynard) 写作时间:2022-04-16
创作不易,未经允许不得转载!!!

Matlab与常微分方程的求解问题,主要分为两个板块:板块一:常微分方程的解析解求解,板块二:常微分方程的数值解的求解,模块三:常微分方程的边界问题【很少有资料介绍这一部分】那么关于这篇博客也是从这两个方面进行matlab与微分方程的求解的介绍的:

一、Matlab与常微分方程的解析解
Matlab 与 常微分方程的解析解的解算主要是依靠一个函数:dsolve,这里的dsolve这个函数在matlab帮助界面中是这么介绍的:

来自于matlab的帮助界面
例子(example problem):
example problem1:最简单的例子
人肉求解:我们但凡学过常微分方程都应该知道这个微分方程的通解的表达式应该是:
matlab code:
syms y(t) %注意这里必须是y(t),代表着y是关于t的函数关系,不能是y t
eqn = diff(y,t,2)-2*diff(y,t,1)+y==0;
solution = dsolve(eqn)result:(与我们人肉计算的结果是一致的)
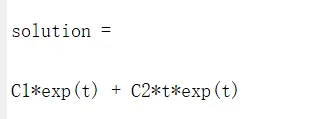
如果存在边界条件的情况,比如对于上面的这个方程如果存在y(0)=1,y'(0)=2的情况,那么我们需要进行如下的尝试:
clear all;close all;clc;
syms y(t)
eqn = diff(y,t,2)-2*diff(y,t,1)+y==0;
Dy = diff(y,t,1);
cond = [y(0)==1,Dy(0)==2];
solution = dsolve(eqn,cond)结果:

结果正确!!!
几个应该注意的点:
1、Dy = diff(y,t,1)这一句是不能省略的,matlab里面是没有默认Dy的定义的,需要你自己去定义
2、边界条件这个东西需要你自己去进行定义,而且边界条件要用[ ]框起来,二阶常微分方程就要两个边界条件确定唯一解,三阶就需要三个,依次类推,如果边界条件不够,就会出现存在待定系数的情况。
解决复杂的常微分方程:
(可以参考:https://blog.csdn.net/weixin_45024585/article/details/107584210)

题目
Matlab code:
syms t y; %声明关键字
u=exp(-5*t)*cos(2*t+1)+5;
uu=5*diff(u,t,2)+4*diff(u,t)+2*u;
y=dsolve(['D4y+10*D3y+35*D2y+50*Dy+24*y=',char(uu)]) % D4y表示y的四阶导具体逻辑和前面说到的那个是类似的,不过就是将非齐次微分方程的右边项单独写出来了
二、Matlab与常微分的数值解
matlab解决常微分方程最有名的就是这个板块了,利用matlab对于常微分方程进行数值求解,主要需要用到的函数就是ode45(一般情况下),如果是求解刚性的微分方程则可以选用ode23,具体微分方程的刚性与否如何判断可以自行检索(这里仅仅附上bing的检索结果):

bing检索结果
简单点来说刚性方程就是时间间隔很小的时候,解才会稳定;如果时间间隔略微大一点,解就不会稳定,目前很难去精确定义那些方程式刚性方程,那些方程是非刚性方程。
更多关于微分方程的刚性与非刚性的资料:https://blog.csdn.net/weixin_34138255/article/details/94112125
这里附上ode系列的列表:
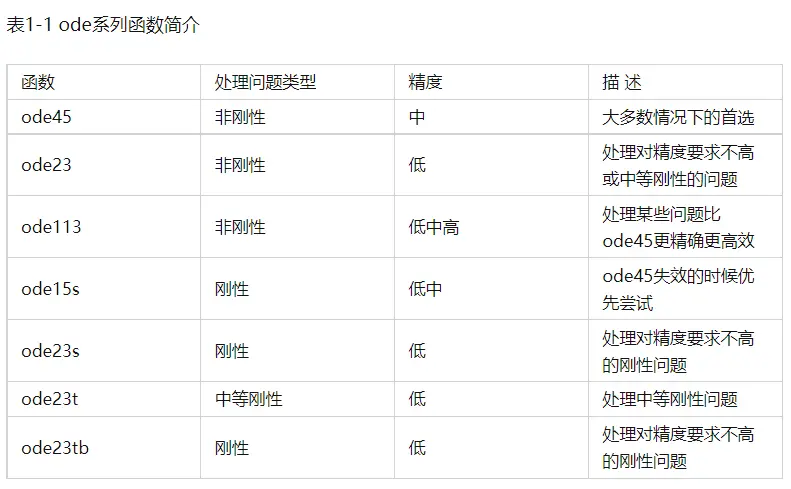
转载自:https://zhuanlan.zhihu.com/p/262021380
ode45方法是使用非刚性的方程:
clear all;close all;clc;
time_array=[0 50];
init_condition = [1;2];
% 错误写法:[t,y]= ode45(@odefunction,'tspan',time_array,'y0',init_condition);
% 这里的tspan是一个具体的函数已经定义死了,所以不需要再键入一个字符串进行索引
[t,y]=ode45(@odefunction,time_array,init_condition);
plot(t,y(:,1),'r')
hold on
plot(t,y(:,2),'b--')
hold off
legend('y','D1y','location','northwest')
function dydt = odefunction(t,y)
dydt = zeros(2,1);
dydt(1)=y(2);
dydt(2)=2*y(2)-y(1);
end几个注意的点:
1、为什么要用dydt,因为matlab中的微分方程只能用y'=f(x,y)的形式表示,所以这里相当于使用了dydt = [y' y''],y=[y y'],所以这里才有dydt(1)=y(2)的等式,同时注意在输出的时候也可以用这样的方式进行与之相应的plot。
2、正如代码里面写到的:
% 错误写法:[t,y]= ode45(@odefunction,'tspan',time_array,'y0',init_condition);
% 这里的tspan是一个具体的函数已经定义死了,所以不需要再键入一个字符串进行索引
注意这一点,这里是因为本人使用plot的时候为了作图好看都要对于参数进行指定养成的习惯,但是这里是不行的!!!
3、注意init_condition = [1;2];这里的初始条件,指定为向量。y0 的长度必须与 odefun 的向量输出相同,使 y0 为 odefun 中定义的每个方程包含一个初始条件。同时这里的【1;2】的含义就是对于tspan的左边值进行的定义其y=1;y’=2 的意思,至于更多的边界问题的求解在第三个模块中可以详见!!!
结果图:

ODE方程求出来的数值解
对比解析解:
clear all;close all;clc;
syms y(t)
eqn = diff(y,t,2)-2*diff(y,t,1)+y==0;
Dy = diff(y,t,1);
cond = [y(0)==1,Dy(0)==2];
solution = dsolve(eqn,cond);
t_span = [0:0.1:50];
y_value = subs(solution,t,t_span);
plot(t_span,y_value)结果图:
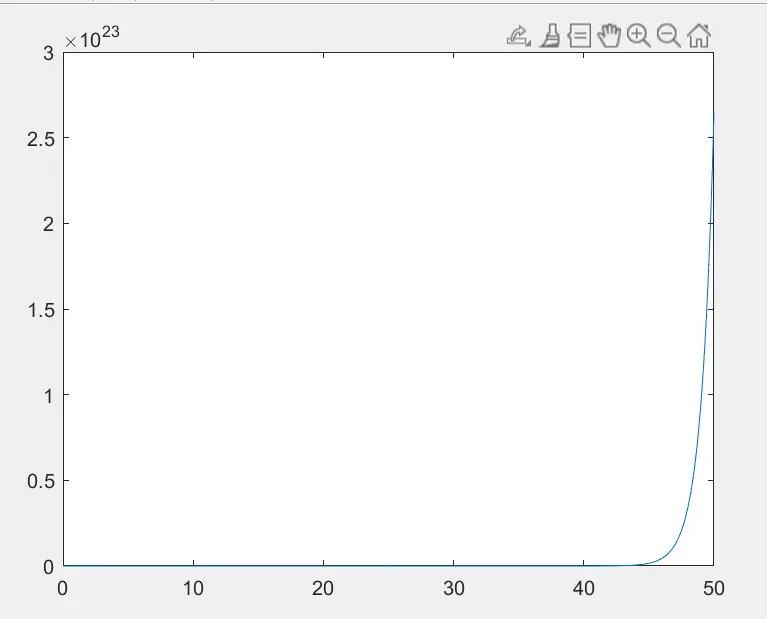
ODE方程求出来的解析解的画图
最终发现这里使用ode45与使用dsolve函数求出来的解析解在图像上的表现是一致的,证明正确。
三、常微分方程与边界问题:
常微分方程与边界问题主要包括在一个函数:bvp4c 这个函数之中,具体的用法可以参考bvp4c 这个函数的帮助页面,然后它具体的使用方法这里用一个案例介绍:
example problem:

题目
matlab 代码:
clear all;close all;clc;
xmesh = linspace(1,2,10);
solinit1 = bvpinit(xmesh,@guess);
sol=bvp4c(@bpv4odeproblem1,@boundaryfunction1,solinit1);
plot(sol.x,sol.y(1,:),'-o')
function yp=bpv4odeproblem1(x,y)
yp=zeros(2,1);
yp(1)=y(2);
yp(2)=2-4*y(1)^2/sin(x)^2;
end
function res = boundaryfunction1(ya,yb)
res = [ya(2)-2*sin(1)*cos(1)
yb(1)-sin(2)^2];
end
function g = guess(x)
g=[ sin(x)
cos(x)];
end几个注意的点:
1、guess 函数可以随便填写,一般不会影响最终的结果(除了一些很特殊的情况)
2、关于bpv4odeproblem1这个函数实际上是跟我们的ode45后面的那个函数的意思是一样的,只要会写ode45的函数这个函数基本就是依葫芦画瓢。
function yp=bpv4odeproblem1(x,y)
yp=zeros(2,1);
yp(1)=y(2);
yp(2)=2-4*y(1)^2/sin(x)^2;
end3、ya与yb的含义,ya和yb实际上是y在上下界的取值,由于y这个相当于一个向量即y=【y,y'】,所以这里为了表示dy/dx(1)则表示为ya(2),ya是下限的意思,2代表第二列,也就是y'的含义。

关于matlab对于微分方程的求解,内容非常繁多,这里仅仅只是冰山一角,更多的知识,如果时间允许,本up主也会持续性更新,谢谢各位捧场!