龙格-库塔法（Runge-Kutta）求解微分方程的Matlab实现

1.软件版本

MATLAB2013b

2.算法理论

龙格－库塔法（Runge-Kutta）是用于模拟​ ​常微分方程​​​的解的重要的一类隐式或显式迭代法。龙格库塔法的家族中的一个成员如此常用，以至于经常被称为“RK4”或者就是“龙格库塔法”。令​ ​初值问题​​表述如下。

这样，下一个值(yn+1)由现在的值(yn)加上时间间隔(h)和一个估算的斜率的乘积决定。该斜率是以下斜率的加权平均：

k1是时间段开始时的斜率；

k2是时间段中点的斜率，通过​ ​欧拉法​​采用斜率k1来决定y在点tn + h/2的值；

k3也是中点的斜率，但是这次采用斜率k2决定y值；

k4是时间段终点的斜率，其y值用k3决定。

3.部分matlab程序

clc;clear;close all;warning off;%The parameter g  = 9.81;L  = 0.1;m  = 0.5;es = 2;%the range of tt0    = 0;tf    = 10;x0    = 0.25;x0dot = 0;Step  = 1000;%The method of RK4 Y1    = func_4RGKT(t0,tf,x0,x0dot,Step);figure(1);subplot(121);plot([t0:(tf-t0)/Step:tf],Y1,'b');xlabel('t');ylabel('x');axis square;grid on;title('the method of RK4');%The method of Euler                         Y2    = func_Euler(t0,tf,x0,x0dot,Step);  figure(1);subplot(122);plot([t0:(tf-t0)/Step:tf],Y2,'r');xlabel('t');ylabel('x');axis square;grid on;title('the method of Euler'); 1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.

function Y1 = func_4RGKT(t0,tf,x0,x0dot,STEPS);                     %t0, tf, upper and lower, respectively,%x0  the initial value of y,%STEPS steps timesh        = (tf - t0)/STEPS;                     T        = zeros(1,STEPS+1);                                  Y        = zeros(1,STEPS+1);T(1)     = t0;                                          Y(1)     = x0;Y0dot(1) = x0dot;for j=1:STEPS                                         tj         = T(j);    yj         = Y(j);    yjd        = Y0dot(j);        k1         = h*func_function(tj     ,[yj,yjd]);        k2         = h*func_function(tj+h/2 ,[yj+h*k1(1)/2,yjd+h*k1(2)/2]);         k3         = h*func_function(tj+h/2 ,[yj+h*k2(1)/2,yjd+h*k2(2)/2]);             k4         = h*func_function(tj+h   ,[yj+h*k3(1)  ,yjd+h*k3(2)]);              Y(j+1)     = yj  + (k1(1) + 2*k2(1) + 2*k3(1) + k4(1))/6;    Y0dot(j+1) = yjd + (k1(2) + 2*k2(2) + 2*k3(2) + k4(2))/6;    T(j+1)     = t0 + h*j;endY1=Y';                  1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.

4.仿真结论

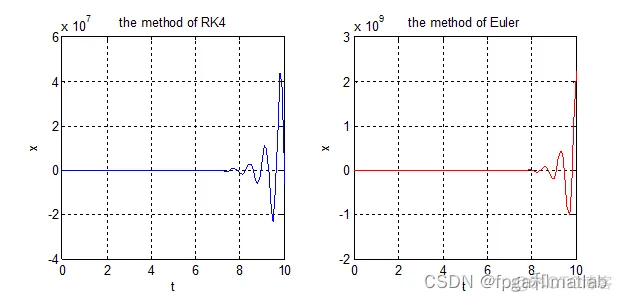
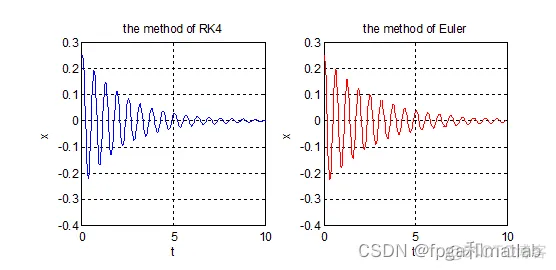
从图的仿真结果可知，当算法迭代1000次的时候，算法经过几个周期抖动之后收敛，但是其收敛时间较短。 因此，从整体而言，采用RK4算法，比Euler算法收敛更快，且较快的达到一定精度之内A28-20。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删