产品
这类复杂方程组，其解方程通常不能直接使用MATLAB内部的自带函数进行求解，往往需要使用别的算法进行，本课题涉及到的方程组的基本类型如下所示：
“连续微分方程”到“离散微分方程”到“差分方程”，离散微分方程，变成差分方程。建立差分方程时，时间采用一阶显格式，空间采用一阶偏心差分格式。
登录后复制
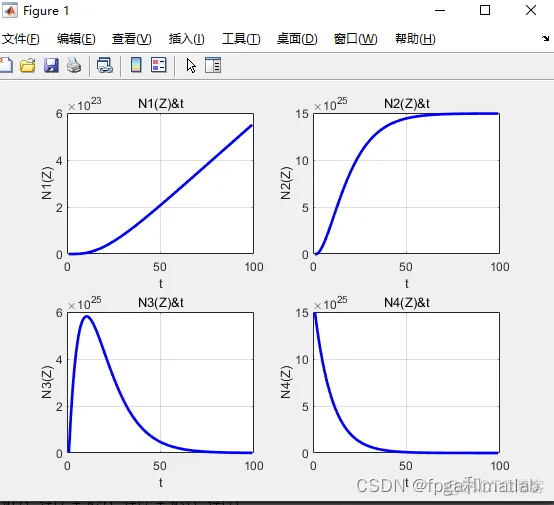
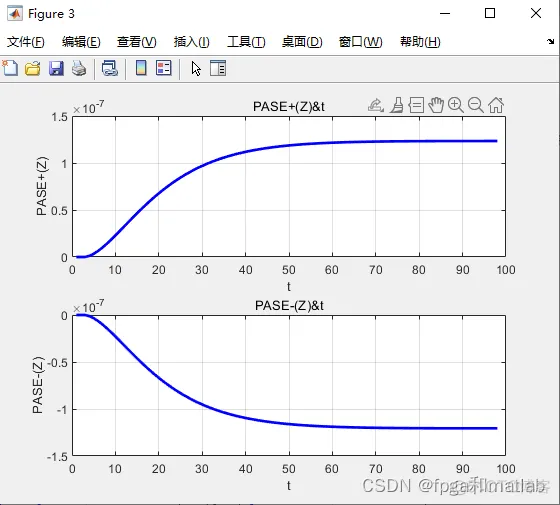
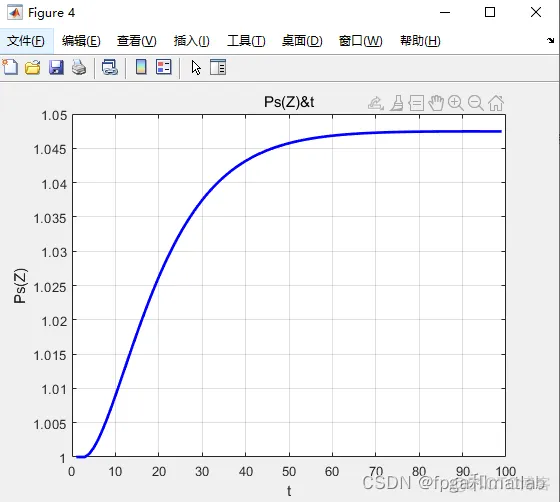
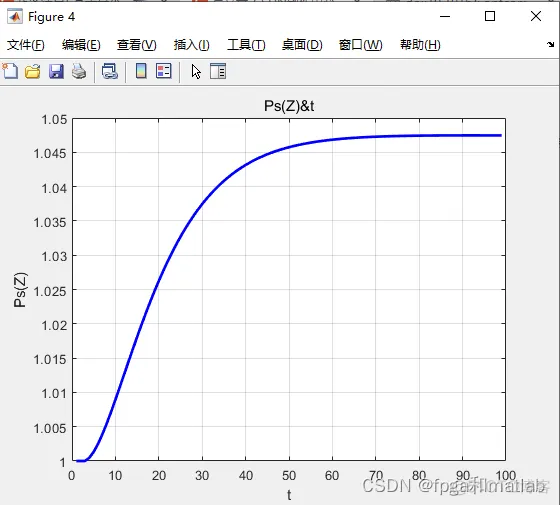
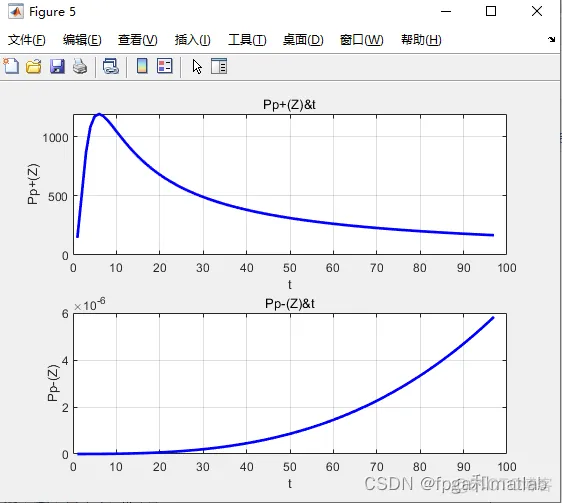
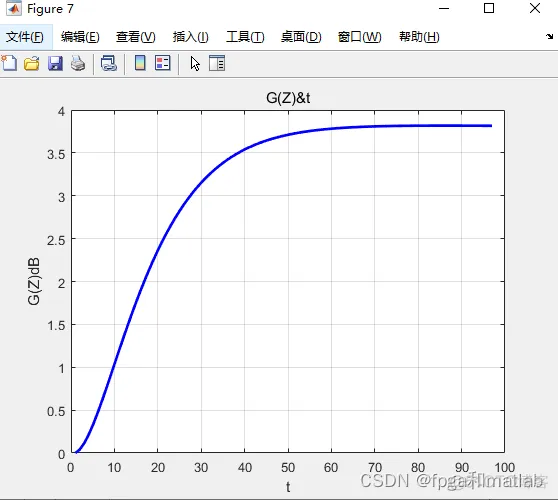
clc;clear;close all;warning off;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%Vj = 1.0e14*[2.037671762107052 2.034215151823580 2.030770248941575 2.027336994082841 2.023915328270042 2.020505192923336 2.017106529857023 2.013719281276238 2.010343389773680 2.006978798326360 2.003625450292398 2.000283289407840 1.996952259783514 1.993632305901912 1.990323372614108 1.987025405136702 1.983738349048801 1.980462150289017 1.977196755152515 1.973942110288066 1.970698162695152 1.967464859721083 1.964242149058149 1.961029978740801 1.957828297142857 1.954637052974735 1.951456195280716 1.948285673436231 1.945125437145175 1.941975436437247 1.938835621665319 1.935705943502825 1.932586352941177 1.929476801287208 1.926377240160643 1.923287621491580 1.920207897518015 1.917138020783374 1.914077944134078 1.911027620717132 1.907987003977725 1.904956047656871 1.901934705789056 1.898922932699921];DVj = 1.0e+011*[3.462483877836962 3.450746652796573 3.439069007521719 3.427450539446898 3.415890849400914 3.404389541572597 3.392946223476911 3.381560505921475 3.370232002973479 3.358960331926962 3.347745113270506 3.336585970655279 3.325482530863469 3.314434423777078 3.303441282347068 3.292502742562887 3.281618443422334 3.270788026901764 3.260011137926652 3.249287424342494 3.238616536886035 3.227998129156823 3.217431857589106 3.206917381424041 3.196454362682216 3.186042466136488 3.175681359285135 3.165370712325313 3.155110198126804 3.144899492206068 3.134738272700597 3.124626220343543 3.114563018438641 3.104548352835411 3.094581911904646 3.084663386514161 3.074792470004828 3.064968858166864 3.055192249216406 3.045462343772321 3.035778844833293 3.026141457755156 3.016549890228479 3.007003852256406];F_ASE_vj = [0.727687625579220 0.726884730352238 0.726081696237599 0.725278527912882 0.724475230042399 0.723671807275757 0.722868264249905 0.722064605587050 0.721260835896694 0.720456959773481 0.719652981799073 0.718848906541101 0.718044738553185 0.717240482375278 0.716436142533662 0.715631723540323 0.714827229893890 0.714022666078659 0.713218036565208 0.712413345810112 0.711608598256263 0.710803798332059 0.709998950452820 0.709194059019136 0.708389128418137 0.707584163022211 0.706779167191096 0.705974145268722 0.705169101586599 0.704364040461595 0.703558966196364 0.702753883079915 0.701948795386920 0.701143707377818 0.700338623299606 0.699533547384828 0.698728483851725 0.697923436905154 0.697118410735281 0.696313409518148 0.695508437416143 0.694703498577095 0.693898597135282 0.693093737210495]; O12_vj = 1.0e-24*[ 0.11 0.13 0.175 0.215 0.3 0.275 0.288 0.31 0.33 0.34 0.335 0.33 0.335 0.33 0.303 0.28 0.25 0.25 0.248 0.26 0.268 0.28 0.325 0.425 0.57 0.628 0.53 0.426 0.388 0.35 0.31 0.25 0.24 0.22 0.195 0.17 0.15 0.14 0.118 0.1 0.078 0.068 0.06 0.059];O21_vj = 1.0e-24*[ 0.05 0.06 0.07 0.095 0.11 0.13 0.15 0.16 0.18 0.2 0.21 0.218 0.23 0.231 0.23 0.228 0.217 0.218 0.225 0.246 0.275 0.318 0.378 0.51 0.76 0.89 0.725 0.638 0.618 0.58 0.527 0.485 0.49 0.475 0.42 0.39 0.365 0.346 0.305 0.262 0.221 0.195 0.17 0.169]; %参数初始化Vp = 3.074794441025641e14;Vs = 1.955593333333334e14;DVs = 3.186042466136488e11;h = 6.626e-34;Ac = 10.5625e-12;Fp = 0.8773;Fs = 0.7078;NEr = 1.5e26;NYb = 1.9e27;O12_vs = 6.5e-25;O21_vs = 9.0e-25;O13_vp = 2.58e-25;O31_vp = 0;O12Yb_vp= 1.0e-24;O21Yb_vp= 1.0e-24; r21 = 7.9e-3; A21 = 1/r21;r32 = 1.0e-9; A32 = 1/r32;r43 = 1.0e-9; A43 = 1/r43;r21Yb = 2.0e-3; A21Yb = 1/r21Yb;C2 = 5.0e-23;C3 = 5.0e-23;C14 = 3.5e-23;Ktr = 2.0e-22;Kba = 0;ap = 0;as = 0;M = 44;%其余参数初始化L = 0.05; %空间长度time = 1e-8; %时间长度Nz = 100; %空间点数Nt = 100; %时间网点数dt = time/Nt;%t微分导数累计量dz = L/Nz;%z微分导数累计量N1 = zeros(Nz,Nt);N2 = zeros(Nz,Nt);N3 = zeros(Nz,Nt);N4 = zeros(Nz,Nt);N1_Yb = zeros(Nz,Nt);N2_Yb = zeros(Nz,Nt);Ps = zeros(Nz,Nt);PASE_plus = zeros(M,Nz,Nt);PASE_minus = zeros(M,Nz,Nt);Pp_plus = zeros(Nz,Nt);Pp_minus = zeros(Nz,Nt); G = zeros(Nz,Nt);NF = zeros(Nz,Nt);%方程组1的式子1复杂系数的参数表示W11 = Fp*O13_vp/(Ac*h*Vp);W12 = Fs*O12_vs/(Ac*h*Vs);for i = 1:M W13(i) = F_ASE_vj(i) * O12_vj(i) / (Ac*h*Vj(i));endW14 = Fs*O21_vs/(Ac*h*Vs);for i = 1:M W15(i) = F_ASE_vj(i) * O21_vj(i) / (Ac*h*Vj(i));endW16 = Fp*O31_vp/(Ac*h*Vp);%方程组1的式子2复杂系数的参数表示W21 = Fs*O12_vs/(Ac*h*Vs);for i = 1:M W22(i) = F_ASE_vj(i) * O21_vj(i) / (Ac*h*Vj(i));endW23 = Fs*O21_vs/(Ac*h*Vs);for i = 1:M W24(i) = F_ASE_vj(i) * O21_vj(i) / (Ac*h*Vj(i));end%方程组1的式子3复杂系数的参数表示W31 = Fp*O13_vp/(Ac*h*Vp); W32 = Fp*O31_vp/(Ac*h*Vp); %方程组1的式子4复杂系数的参数表示W41 = Fp*O12Yb_vp/(Ac*h*Vp);W42 = Fp*O21Yb_vp/(Ac*h*Vp);Ps(1,:) = ones(1,Nt);Pp_plus(1,:) = ones(1,Nt);Pp_minus(1,:) = ones(1,Nt);for j = 1:Nt-1 for i = 1:Nz-1 %方程组1式子1 N1(i,j+1) = N1(i,j) + ... dt*( -1*(W11*(Pp_plus(i,j) + Pp_minus(i,j)) + W12*Ps(i,j) + sum(W13.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))'))*N1(i,j) +... (A21 + W14*Ps(i,j) + sum(W15.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))'))*N2(i,j) + ... C2*N2(i,j)^2 + W16*(Pp_plus(i,j) + Pp_minus(i,j))*N3(i,j) + C3*N3(i,j)^2 - C14*N1(i,j)*N4(i,j)+... -1*Ktr*N2_Yb(i,j)*N1(i,j)+Kba*N1_Yb(i,j)*N3(i,j) ); %方程组1式子2 N2(i,j+1) = N2(i,j) + ... dt*( (W21*Ps(i,j)+sum(W22.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))'))*N1(i,j) +... -1*(A21 + W23*Ps(i,j) + sum( W24.*(PASE_plus(:,i,j)+PASE_minus(:,i,j))' ))*N2(i,j) +... A32*N3(i,j) - 2*C2*N2(i,j)^2 + 2*C14*N1(i,j)*N4(i,j) ); %方程组1式子3 N3(i,j+1) = N3(i,j) + ... dt*( W31*(Pp_plus(i,j) + Pp_minus(i,j))*N1(i,j) - A32*N3(i,j) - W32*(Pp_plus(i,j) + Pp_minus(i,j))*N3(i,j) -... 2*C3*N3(i,j)^2 + A43*N4(i,j) + Ktr*N2_Yb(i,j)*N1(i,j) - Kba*N1_Yb(i,j)*N3(i,j) ); %方程组1式子4 N1_Yb(i,j+1) = N1_Yb(i,j) + ... dt*(-1*W41*(Pp_plus(i,j) + Pp_minus(i,j))*N1_Yb(i,j) + W42*(Pp_plus(i,j) + Pp_minus(i,j))*N2_Yb(i,j) +... A21Yb*N2_Yb(i,j) + Ktr*N2_Yb(i,j)*N1(i,j) - Kba*N1_Yb(i,j)*N3(i,j)); %方程组1式子5 N4(i,j+1) = NEr - (N1(i,j+1) + N2(i,j+1) + N3(i,j+1)); %方程组1式子6 N2_Yb(i,j+1) = NYb - N1_Yb(i,j+1); if N1(i,j+1) > NEr,N1(i,j+1) = NEr;end if N2(i,j+1) > NEr,N2(i,j+1) = NEr;end if N3(i,j+1) > NEr,N3(i,j+1) = NEr;end if N4(i,j+1) > NEr,N4(i,j+1) = NEr;end if N1_Yb(i,j+1) > NYb,N1_Yb(i,j+1) = NYb;end if N2_Yb(i,j+1) > NYb,N2_Yb(i,j+1) = NYb;end if N1(i,j+1) < 0,N1(i,j+1) = 0;end if N2(i,j+1) < 0,N2(i,j+1) = 0;end if N3(i,j+1) < 0,N3(i,j+1) = 0;end if N4(i,j+1) < 0,N4(i,j+1) = 0;end if N1_Yb(i,j+1) < 0,N1_Yb(i,j+1) = 0;end if N2_Yb(i,j+1) < 0,N2_Yb(i,j+1) = 0;end %由以上方程计算得到的N1，N2，N3，N4，N1Yb，N2Yb %方程组2 Pp_plus(i+1,j) = Pp_plus(i,j) + dz*(-Fp*(O13_vp*N1(i,j) - O31_vp*N3(i,j) + O12Yb_vp*N1_Yb(i,j) - O21Yb_vp*N2_Yb(i,j))*Pp_plus(i,j) - ap*Pp_plus(i,j)); Pp_minus(i+1,j) = Pp_minus(i,j) + dz*(Fp*(O13_vp*N1(i,j) - O31_vp*N3(i,j) + O12Yb_vp*N1_Yb(i,j) - O21Yb_vp*N2_Yb(i,j))*Pp_minus(i,j) + ap*Pp_plus(i,j)); Ps(i+1,j) = Ps(i,j) + dz*(Fs*( O21_vs*N2(i,j) - O12_vs*N1(i,j) )*Ps(i,j) - as*Ps(i,j)); %PASE_plus = zeros(M,Nz,Nt); %PASE_minus = zeros(M,Nz,Nt); for ii = 1:M PASE_plus(ii,i+1,j) = PASE_plus(ii,i,j)+dz*(F_ASE_vj(ii)*( O21_vj(ii)*N2(i,j) - O12_vj(ii)*N1(i,j) ) * PASE_plus(ii,i,j) +... 2*h*Vj(ii)*DVj(ii)*F_ASE_vj(ii)*O21_vj(ii)*N2(i,j)-as*PASE_plus(ii,i,j)); PASE_minus(ii,i+1,j) = PASE_minus(ii,i,j)+dz*(-1*F_ASE_vj(ii)*( O21_vj(ii)*N2(i,j) - O12_vj(ii)*N1(i,j) ) * PASE_minus(ii,i,j) -... 2*h*Vj(ii)*DVj(ii)*F_ASE_vj(ii)*O21_vj(ii)*N2(i,j)+as*PASE_minus(ii,i,j)); end if Pp_plus(i+1,j) < 0,Pp_plus(i+1,j) = 0;end if Pp_minus(i+1,j) < 0,Pp_minus(i+1,j) = 0;end if Ps(i+1,j) < 0,Ps(i+1,j) = 0;end %通过稳态计算得到Pp+，Pp-，Pase+，Pase-，Ps endendfor z = 1:Nz for t = 1:Nt PASE_plus2(z,t) = sum(PASE_plus(:,z,t)); PASE_minus2(z,t) = sum(PASE_minus(:,z,t)); endendfor z = 1:Nz for t = 1:Nt G(z,t) = 10*log10(Ps(z,t)/Ps(1,1)); endendfor z = 1:Nz for t = 1:Nt NF(z,t) = 10*log10(1/G(z,t) + PASE_plus2(z,t)/(G(z,t)*Vs*DVs) ); endend%计算得到N1~t，N2~t，N3~t，N4~t，........figure;subplot(221);plot(N1(1,2:end),'b-','LineWidth',2);xlabel('t');ylabel('N1(Z)');title('N1(Z)&t');grid on;subplot(222);plot(N2(1,2:end),'b-','LineWidth',2);xlabel('t');ylabel('N2(Z)');title('N2(Z)&t');grid on;subplot(223);plot(N3(1,2:end),'b-','LineWidth',2);xlabel('t');ylabel('N3(Z)');title('N3(Z)&t');grid on;subplot(224);plot(N4(1,2:end),'b-','LineWidth',2);xlabel('t');ylabel('N4(Z)');title('N4(Z)&t');grid on;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%figure;subplot(211);plot(N1_Yb(1,2:end),'b-','LineWidth',2);xlabel('t');ylabel('N1Yb(Z)');title('N1Yb(Z)&t');grid on;subplot(212);plot(N2_Yb(1,2:end),'b-','LineWidth',2);xlabel('t');ylabel('N2Yb(Z)');title('N2Yb(Z)&t');grid on;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%figure;subplot(211);plot(PASE_plus2(3,1:end-2),'b-','LineWidth',2);xlabel('t');ylabel('PASE+(Z)');title('PASE+(Z)&t');grid on;subplot(212);plot(PASE_minus2(3,1:end-2),'b-','LineWidth',2);xlabel('t');ylabel('PASE-(Z)');title('PASE-(Z)&t');grid on;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%figure;plot(Ps(2,1:end-1),'b-','LineWidth',2);xlabel('t');ylabel('Ps(Z)');title('Ps(Z)&t');grid on;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%figure;subplot(211);plot(Pp_plus(20,3:end-1),'b-','LineWidth',2);xlabel('t');ylabel('Pp+(Z)');title('Pp+(Z)&t');grid on;subplot(212);plot(Pp_minus(20,3:end-1),'b-','LineWidth',2);xlabel('t');ylabel('Pp-(Z)');title('Pp-(Z)&t');grid on;figure;subplot(211);plot(Pp_plus(1:end,6),'b-','LineWidth',2);xlabel('t');ylabel('Pp+(Z)');title('Pp+(Z)&t');grid on;subplot(212);plot(Pp_minus(1:end,6),'b-','LineWidth',2);xlabel('t');ylabel('Pp-(Z)');title('Pp-(Z)&t');grid on;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%figure;plot(G(20,3:end-1),'b-','LineWidth',2);xlabel('t');ylabel('G(Z)dB');title('G(Z)&t');grid on; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%figure;plot(NF(2,3:end-1),'b-','LineWidth',2);xlabel('t');ylabel('NF(Z)dB');title('NF(Z)&t');grid on;1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.80.81.82.83.84.85.86.87.88.89.90.91.92.93.94.95.96.97.98.99.100.101.102.103.104.105.106.107.108.109.110.111.112.113.114.115.116.117.118.119.120.121.122.123.124.125.126.127.128.129.130.131.132.133.134.135.136.137.138.139.140.141.142.143.144.145.146.147.148.149.150.151.152.153.154.155.156.157.158.159.160.161.162.163.164.165.166.167.168.169.170.171.172.173.174.175.176.177.178.179.180.181.182.183.184.185.186.187.188.189.190.191.192.193.194.195.196.197.198.199.200.201.202.203.204.205.206.207.208.209.210.211.212.213.214.215.216.217.218.219.220.221.222.223.224.225.226.227.228.229.230.231.232.233.234.235.236.237.238.239.240.241.242.243.244.245.246.247.248.249.250.251.252.253.254.255.256.257.258.259.260.261.262.263.264.265.266.267.268.269.270.271.272.273.274.275.276.277.278.279.280.281.282.283.284.285.286.287.288.289.290.291.292.293.294.295.296.297.298.299.300.301.302.303.304.305.306.307.308.309.310.311.312.313.314.315.316.317.318.319.320.321.322.323.324.325.326.327.328.329.330.331.332.333.334.335.336.337.338.339.340.341.342.343.344.345.346.347.348.349.350.351.352.353.354.355.356.357.358.359.360.361.362.363.364.365.366.367.368.369.370.371.372.373.374.375.376.377.378.379.380.381.382.383.384.385.386.387.388.389.390.391.392.393.394.395.396.397.398.399.400.401.402.403.404.405.406.407.408.409.410.411.412.413.414.415.416.417.418.419.420.421.422.423.424.425.426.427.428.429.430.431.432.433.434.435.436.437.438.439.440.441.442.443.444.445.446.447.448.449.450.451.452.453.454.455.456.457.458.459.460.461.462.463.464.465.466.467.468.469.470.471.472.473.474.475.476.477.478.479.480.481.482.483.484.485.486.487.488.489.490.491.492.493.494.495.496.497.498.499.500.501.502.503.504.505.506.507.508.509.510.511.512.513.514.515.516.517.518.519.520.521.522.523.524.525.526.527.528.529.530.531.532.533.534.535.536.
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
